李岳，韩宾，鲁云

　　（西南科技大学 信息工程学院，四川 绵阳 621010）

       摘要：介绍了短时傅里叶变换、Cohen类时频分布、小波变换、Hilbert-Huang变换四种典型的时频分析方法，分析对比结果显示了用Hilbert-Huang变换对声音信号进行时频分析的优越性，结合LabVIEW在数据采集和仪器控制领域的强大功能，提出以声卡作为采集硬件、LabVIEW作为软件编程、Hilbert-Huang变换作为时频分析方法的一种声音信号采集分析系统。实验结果表明，这种采集分析系统非常适合频率在音频范围之内（20 Hz~20 kHz）的声音信号的时频谱分析。

　　关键词：声卡；LabVIEW；时频分析；EMD

0引言

　　声音信号如同其他自然界的信号和人工合成的信号一样，都是典型的非平稳信号，其明显的特点是信号是时变的且信号持续时间是有限的。想要从真实信号中提取出不同组成成分的时变信息，一般的做法是通过时频分析方法将低维的一维时间信号映射到二维的时间-频率函数空间，其目的是揭示信号包含了多少频率分量以及各个频率分量是如何随时间变化的。

　　声卡作为一个常见的计算机配置，其本身就是一个非常优秀的数据采集系统，它搭载的A/D和D/A转换器可以很方便地实现模拟信号和数字信号的相互转换。如果被测对象的频率在音频范围之内（20 Hz~20 kHz），而且对采样频率没有特别高的需求，则可以用计算机自带的声卡来构建一个数据采集系统。而LabVIEW由于其直观的编程方式和强大的功能函数库等特点，已经广泛地被各界科研工作者和工程师们所采用，也被视为标准的仪器控制和数据采集软件。通过声卡和LabVIEW的联合开发，能够对声音信号进行数据采集、数据保存、波形显示、信号分析等功能。

　　本文分析对比了四种典型的时频分析方法：短时傅里叶变换、Cohen类时频分布、小波变换、Hilbert-Huang变换，通过调频合成信号的理论计算，阐述了四种方法的优缺点。并且以计算机自带的声卡为硬件平台，以LabVIEW作为软件平台，设计开发了一种高效低成本的声音信号的经验模态分解（Empirical Mode Decomposition，EMD）时频分析的系统。通过实验表明，把信号进行EMD分解得到信号的时频分布，对信号有很强的自适应性，能够很好地处理非线性、非平稳的信号。

1时频分析理论基础

　　1.1短时傅里叶变换

　　短时傅里叶变换（ShortTime Fourier Transform，STFT）是1946年Gabor提出来的，基本思想是在信号进行傅里叶变换之前先乘以一个时间有限的窗函数，并假定信号在窗内是平稳的，以此来确定窗内存在的频率成分，然后通过窗在时间轴上的移动逐段分析信号，最后得到所需的时频分布［1］。信号x(t)的短时傅里叶变换为：

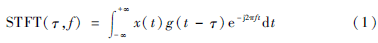
　　式（1）中，x(t)为被分析的信号，g(t)为窗函数，当窗函数g(t)取值为常数1时，短时傅里叶变换退化为传统的傅里叶变换。

　　短时傅里叶的反变换为：

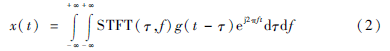
　　1.2Cohen类时频分布

　　Cohen在20世纪60年代中期发现众多的时频分布只是WignerVille时频分布的变形，可以用一个统一的形式表示，习惯称之为Cohen类时频分布［2］，其表达式为：

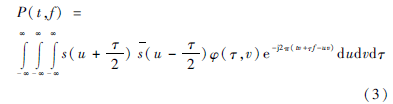
　　式（3）中,φ(τ,v)为核函数，当其取值为1时，Cohen类时频分布退化为WignerVille时频分布。

　　常用的加上核函数之后的Cohen类时频分布有BornJordan分布（BJD）、伪WignerVille时频分布（PWD）、平滑WignerVille时频分布（SPWD）。

　　1.3小波变换

　　小波变换是一个较新的应用数学分支，在20世纪80年代后期工程应用的需求促使其迅速发展起来。法国学者I.Daubechies和S.Mallat把这一理论应用到工程应用领域。其在信号处理领域起到非常重要的作用［3］。

　　信号x(t)的连续小波变换为：

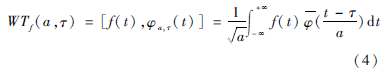
　　式（4）中，φ(t)是母小波函数，φ(t)是φ(t)的共轭函数，τ是平移因子，a是尺度因子［3］。连续小波变换的逆变换为：

　　式（5）中，Cφ=∫+∞0|ψ(aw)|2ada<∞，是φ(t)需要满足的容许条件。

　　1.4HilbertHuang变换

　　HilbertHuang变换是N.E.Huang等人在1998年首次提出的，它通过提取信号上下包络的均值，反复筛选，自适应地得到一系列的时域局部对称且瞬时频率具有明确物理意义的IMF（Intrinsic Mode Function）信号，能解决Hilbert变换不能处理多值频率的信号的问题［4］。

　　HilbertHuang变换包含2个主要步骤:

　　(1) 对原始数据进行经验模态分解（EMD）的预处理，把数据分解为满足Hilbert变换所要求的n阶固有模式函数(IMF)和残余函数之和。

　　(2) 对每一阶IMF进行Hilbert变换，得到瞬时频率，从而求得时频分布［4］。

2几种时频分析比较

　　本文用一个正向和一个反向的高斯型调频信号叠加成一个合成信号来检验几种时频分析方法的应用效果。在0~2 000 ms时间段由中心点1 000 ms、频率为180 Hz的一个高斯型调频信号叠加另一个中心点1 000 ms、频率为50 Hz的高斯型调频信号，两个高斯型调频信号的频率都是在50 Hz~180 Hz之间变化，并且在287 ms~318 ms和1 679 ms~1 710 ms时间段叠加了两个频率为常数156 Hz的信号（图1、图2所示）。

　　分别对图1中的信号进行短时傅里叶变换、Cohen类时频分布、小波变换和HilbertHuang变换，其时频分析结果如图3~图6。图3短时傅里叶变换图3中，其窗函数选用的是65点的hanning窗，可以从时频变换结果看出，短时傅里叶变换在一定程度上弥补了传统的傅里叶变换不具备局部频率分析的能力。但是，短时傅里叶变换还是通过滑动时间窗来计算信号的频谱，其必然会受到Heisenberg测不准原理的约束［5］，也就是长窗口有高的频率分辨率和低的时间分辨率而短窗口有高的时间分辨率和低的频率分辨率，即选用的窗函数确定之后，对应的时频分辨率就是固定的，而窗函数的时间分辨率和频率分辨率并没有随着信号频率的变化而自适应地变化。所以，在信号的大概频率未知的情况下，选择合适的窗函数是非常关键的步骤。

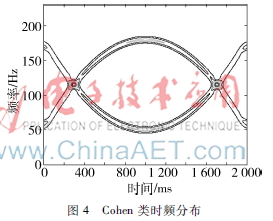
　　图4是对信号进行Cohen类时频分布分析的结果，可以看出分析结果有很好的时频聚焦特性。但是，由于Cohen类时频分布本身有交叉项的影响，会降低时频分辨率。如图4所示，在287 ms~318 ms和1 679 ms~1 710 ms时间段叠加的两个常数频率就被掩盖了图4Cohen类时频分布。所以，虽然Cohen类时频分布有非常好的时频聚焦性，但是由于其固有交叉项的干扰，其应用效果受到影响。

　　图5是对信号进行连续小波变换分析的结果，连续小波变换能够随频率的变化自适应变化其时频分辨率，即在低频部分有很好的频率分辨率，在高频部分有很好的时间分辨率，解决了短时傅里叶变换在时域和频域上不能同时自图5连续小波变换适应变化的问题。但是，如图5所示，连续小波变换时频分析结果的时频聚焦性不好。而且，图6HilbertHuang变换连续小波变换的小波基一旦确定，在整个分析过程中就无法被替换，所确定小波基的类型直接影响到信号分析的效果，如何判断和选用合适的小波基来分析信号是一个难点。

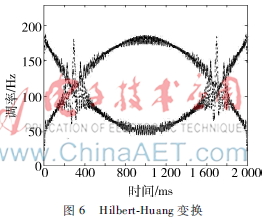
　　图6是对信号进行HilbertHuang变换分析的结果，可以看出HilbertHuang变换不再受傅里叶变换的限制，不需要预先设置基函数，能够根据信号自身的特点自适应地选择频带，其分析结果有良好的时频聚焦特性，在一定程度上改善了小波分析结果的模糊性，适用于分析非线性、非平稳的信号。HilbertHuang变换作为一种较新的信号分析方法，其基本理论还不是很完善，还需要一些准确的定义上的证明［6］。但是，HilbertHuang变换良好的自适应性和更精确的时频分辨率使其在处理非平稳信号时具有出色的表现，已经引起了工程师和科研工作者的广泛关注［7］。

3声卡和LabVIEW结合实现EMD时频分析

　　常用的声卡能够对声音信号进行双声道16位的数据采集，而且采集到的数据是高保真的，最高采样率能够达到176.4 kHz，这样一个较高的采样精度和采样率，能够满足大多数科研和工程测量的需求。值得注意的是，声卡的输入端电压不要超过1 V。

　　LabVIEW提供了许多便于对声卡操作的函数，通过在LabVIEW后面板调用底层的声卡操作函数来实现对声音信号的采集。LabVIEW还提供了MATLAB程序调用接口MATLAB Script，立足于LabVIEW自身数据采集、数据保存、波形显示的优势，结合MATLAB强大的数值计算能力，就可以快速地开发出一个声音信号采集分析系统。

　　图7是LabVIEW声音采集分析程序，包含了配置声音参数、写入声音文件、声音文件波形、调用MATLAB Script进行EMD时频分析、声音文件存储等功能。在实验室环境下，对两个周期的规律性变化的声音信号进行采集和EMD时频分析。

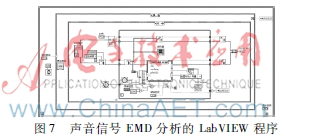
　　图8是实验室环境下基于声卡和LabVIEW采集到的声音信号的时域波形，图9是EMD时频分析的结果。从实验结果可以看到，在采集到的0~6 s时间段一直存在一个20 Hz左右的低频信号，采集到的高频噪声由滤波器滤除，信号经过大约0.5 s的时间，幅值会有一个较大的变化，图8采集的声音信号时域波形会有一个强信号的输入，频率大概在100 Hz~450 Hz之间，而且在这个0~6 s时间段大约有两个周期的信号在波动。

4结论

　　本文提出了一种基于声卡和LabVIEW对声音信号进行图9EMD时频分析结果EMD时频分析的系统，这种系统非常适合对频率在音频范围之内（20 Hz~20 kHz）的声音信号进行频谱分析，分析结果有良好的时频聚焦性，对信号有非常好的自适应能力。但是，HilbertHuang变换是一种较新的信号分析方法，其自身理论还在发展构建当中，一些相关的理论完善工作还有待进一步开展。

参考文献

　　［1］ DURAK L. Shiftinvariance of shorttime Fourier transform in fractional Fourier domains ［J］. Journal of the Franklin InstituteEngineering and Applied Mathematics, 2009, 346(2): 136146.

　　［2］ Wang Yan, Wu Xi, Li Wenzao, et al. Analysis of microdoppler signatures of vibration targets using EMD and SPWVD ［J］. Neurocomputing, 2016(171): 4856.［3］ IGLEWSKANOWAK I. Continuous wavelet transforms on ndimensional spheres ［J］. Applied and Computational Harmonic Analysis, 2014,39(2): 248276.

　　［4］ HUANG N E, SHEN Z, LONG S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］. Proc. R. Soc. London. A,1998, 454（1971）: 903995.

　　［5］ 杨建国．小波分析及其工程应用［M］ ．北京：机械工业出版社，2005.

　　［6］ 苗晟，王威廉，姚绍文．HilbertHuang变换发展历程及其应用［J］. 电子测量与仪器学报，2014,28(8)：812818．

　　［7］ 胡爱军．HilbertHuang变换在旋转机械振动信号分析中的应用研究［D］ 北京：华北电力大学，2008.