孙少乙1,2,黄志波1
(1.华北计算机系统工程研究所,北京 100083;2.中电和瑞科技有限公司,北京 100083)
摘要:为了使用支持向量机(SVM)算法进行多类分类,在SVM二分类基础上,提出使用排序算法中冒泡排序的思想进行SVM多类别数据分类。使用该方法在选取的UCI数据集进行实验,结果表明,在保证较高正确率的情况下,相对传统一对一的多分类方法,该方法较大幅地减少了分类时间,是一种应用性较强的SVM多类分类方法。
关键词:支持向量机;多类分类;冒泡排序; LibSVM
0引言
支持向量机(Support Vector Machine,SVM) 是一种在统计学习基础上发展起来的机器学习方法,其最大特点是根据Vapnik结构风险最小化原则[1]。它的基本模型是定义在特征空间上的间隔最大的线性分类器[2],在解决小样本、非线性及高维度等问题上具有传统的机器学习方法所不具备的优势[3]。SVM本是针对二分类问题提出的,如何将其应用到多类分类问题将成为对SVM研究的重要问题之一。当前,对于SVM的多分类问题,解决思路有两种:(1)将问题转化为SVM直接可解的问题;(2)适当改变原始SVM中最优化问题,使之成为能同时计算出所有分类决策问题的决策函数,从而一次性实现多分类。其中方法(2)看似简单,但由于其问题最优化求解过程太过复杂,计算量太大,实现困难,未得到广泛应用[4]。故当前多分类主要采用的是方法(1)的思想。
1SVM原理及多分类方法
1.1SVM分类原理
假设给定一个特征空间的含有N个样本的训练数据集T={(X1, Y1),(X2, Y2),…,(XN, YN)},其中,Xi∈Rn,Yi∈{+1,-1},i=1,2,3,…,N,Xi为第i个特征向量,Yi为Xi的类标记,即Yi=+1时,Xi为正例,Yi=-1时,Xi为反例。SVM就是要找到一个超平面ω·X+b=0,能将两类样本分开,并且超平面距两类样本的间隔最大,这样可以将超平面用于对未知样本进行分类,并且使错误最小化。
由于函数间隔可以根据ω和b等比例地放大和缩小,而几何间隔不会,故选择几何间隔作为要最大化的间隔距离。为使间隔最大化,问题可以表示为在式(2)的条件下求式(1)的最小化问题。
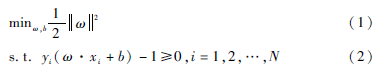
求得最优解ω′、b′,得到超平面ω′·x+b′=0即最大间隔分离面。
样本线性不可分时,存在某些样本点(xi,yi)不能满足函数间隔大于等于1的约束条件(2)。为此,在每个样本点(x,yi)加入一个松弛变量δi≥0,约束条件变为
yi(ω·xi+b)≥1-δi
同时,对每个松弛变量δi添加一个代价δi,故问题转化为:
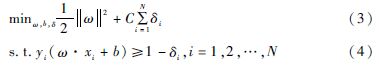
δi≥0,i=1,2,…,N(5)
这里C为惩罚因子,根据具体问题而定。
1.2SVM的多分类方法
上文提到的SVM的多分类方法(2)未能得到广泛应用,故这里只对方法(1)进行阐述。将多分类问题转化为多个SVM直接可解的二分类问题,主要有“oneagainstrest”(1ar)、“oneagainstone”(1a1)和DAG SVM[5]。
1ar方法构建k个二类分类器,每个分类器都是其中一类(正类)对其他所有类(负类)。分类时,分别计算各个分类器的决策函数值,取测试函数值最大的对应类别为测试数据类别[6]。该方法在分类时需使用k个判别函数进行判别。当训练样本较大时,训练较为困难[7]。
1a1方法由KNERR提出,该方法对k类的每两个类构造一个分类器,共构造k(k-1)/2个子分类器。对未知样本分类时,每个子分类器都进行判别,故需使用k(k-1)/2个判别函数进行判别,结果对相应类别投一票,最终统计得票数,票数最多的类为未知样本所属类别。由于测试时要对任意类进行比较,训练和预测速度随类别数成指数增长[8]。
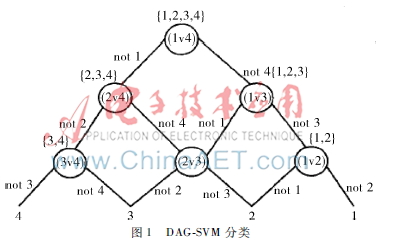
DAGSVMS方法由PLATT J C等人提出的决策导向的循环图DDAG导出,是针对1vs1SVMS存在误分、拒分现象提出的[9]。该算法在训练阶段也要构造k(k-1)/2个子分类器,这些子分类器构成一个有向无环图。分类时,首先从顶节点开始,根据分类结果进入下一层节点,继续分类直到叶节点。该方法在分类时需使用k-1个判别函数进行判别。由于它采取的是排除策略,如果在开始阶段就决策错误的话,那么后面的步骤都没有意义了[10]。图1是采用DAGSVM对4类样本分类决策过程示意图。
2基于冒泡的多分类思想
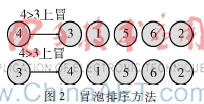
本文提出一种冒泡的SVM多分类方法,其受启发于排序算法中的冒泡排序。在冒泡排序算法中,内层循环是大者上浮或小数下沉(这里用大数据上浮),将本次冒泡中最大的数逐渐上冒,放到最大的位置。如图2所示,在第一次冒泡中,第一个节点值为4大于第二个节点,故节点4上冒;下一次冒泡中,第二个节点4大于第三节点1,值4节点继续上冒,依次下去,一轮完成后最大值冒到最右边位置,即找到图2例中的值为6的节点为最大值。
相对于具体数值而言,SVM多分类中的每个类别没有具体的值,但是两个类别之间的大小关系是可以区分的,即为一个SVM的二分类结果。即如果有一个待预测数据x,使用类别1和类别2训练样本训练出来的分类模型对其进行分类,分类器将其分类为类别2,笔者认为针对于样本x而言,类2大于类1。有了相对大小之后,就可以像冒泡排序那样进行冒泡了,一轮下来,针对样本x的最大的类别yi冒到最右端,则认为x属于yi。
如图3所示,类别标签从1~6,类别标签后边的值是针对待分类样本x各个类别之间的相对虚拟值。如此图分类下来,最终样本x被分类为类别5。
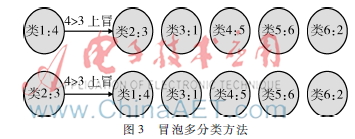
若多分类类别有C个,则需要进行C-1个SVM二分类来对一个样本进行分类,这同DAG SVM是一样的。同时,与1a1和DAG SVM的分类方法一样,该方法需要训练出C·(C-1)/2个分类模型。从算法训练和分类计算复杂度来说,该方法与DAG SVM相同。
同时该方法可以对类别分组冒泡,即先将所有类别分成若干组,每个组分别冒泡,从每个组中选出改组中相对样本x最大的组,然后将每组中选出的类别再分组,再从每组中选出最大类别,如此进行下去,直到最后选出所有组的最大类别标签,即是样本x的类别。仍用上边的例子,如图4所示,将6个类别分成两组,类标签为1、2、3的为一组,类标签为4、5、6为一组,第一组冒泡分类,选出类1,第二组冒泡分类选出类5,然后类1和类5再进行SVM二分类,最终选出类5,则样本x被分为第5类。
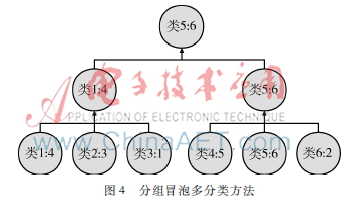
图4分组冒泡多分类方法这样分组的好处是可以使分类算法并行进行分类,加快分类速度。如上例,第一组和第二组的冒泡过程各自独立,可以进行多个线程或者多个进程的并行执行,最后将各自的结果汇总再分类。这种方法可以充分利用现在计算机多核和多台计算机并行运算的特点。
3实验及结果分析
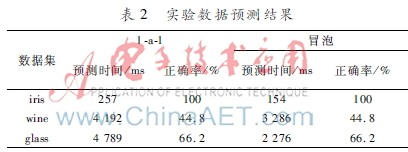
为了比较1-a-1与冒泡 SVM多分类方法的性能,选取了UCI机器学习数据库中3个数据集进行试验,3个数据集分别为iris、wine和glass。表1列出了数据集实例数、属性数和类个数。表1数据集信息数据集实例数类个数属性数iris15035wine178314glass214610LibSVM库已被广泛应用到多个领域[11]。实验使用了LibSVM(版本3.2)库进行SVM二分类的训练和预测。为了减小实验误差,实验中没有使用LibSVM自身的1-a-1多分类,而是分别重写1-a-1和冒泡函数,它们都调用LibSVM库的基本二分类算法。训练时使用的SVM类型为LibSVM的CSVC,其中设C=4,其他均为默认值。实验使用所选数据集的2/3做训练数据,剩下的1/3留做预测数据,最后由运行结果对1-a-1与冒泡的预测时间和分类精确度进行了对比。实验结果见表2,表中为根据以上方法对1-a-1与冒泡多分类方法的预测时间和正确率的对比。

实验结果表明,冒泡的多分类方法可以在轻微影响分类正确率的情况下极大地降低新样本的预测时间。理论上看,冒泡多分类方法在训练上与1-a-1方法相同,而在预测新样本时,二分类次数由C(C-1)/2降低为C-1,从而减少了预测分类时间。
4结论
本文提出的冒泡SVM多分类方法受启发于排序算法中的冒泡排序方法,多类分类时较1a1方法有较少的二分类次数,减少了分类时间,同时其分组冒泡分类更可以利用现在计算机并行计算的特点提高分类效率。该方法的一个缺点是,分类时如果有一个二分类结果错误,则最终结果就会错误,有待进一步改进。
参考文献
[1] VLADIMIR N V. An overview of statistical learning theory[J]. IEEE Transactions on Neural Networks, 1999,10(5):988989.
[2] 李航. 统计学习方法[M]. 北京:清华大学出版社, 2012.
[3] 奉国和. 四种分类方法性能比较[J]. 计算机工程与应用,2011,47(8):2526,145.
[4] 杨国鹏,余旭初,陈伟,等. 基于核Fisher判别分析的高光谱遥感影像分类[J]. 遥感学报, 2008,12(4):579585.
[5] 周爱武, 温春林, 王浩. 基于二叉树的SVM多类分类的研究与改进[J]. 微型机与应用, 2013, 32(12):6769.
[6] 刘勇,全廷伟. 基于DAGSVMS的SVM多类分类方法[J]. 统计与决策, 2007(20):146148.
[7] VOJTECH F,VACLAV H.Multiclass support vector machine[C]. Proceedings of the 16th International Conference on Pattern Recognition, 2002:236239.

