韩芳，陈帅

　　（淮南师范学院 机械与电气工程学院，安徽 淮南 232038）

       摘要：根据余数系统中模映射法则以及数论变换，将素数N点的DFT运算转换为N-1点的循环卷积运算，建立了算法模型，给出了此算法的FIR滤波器图解，并对加法器系数进行RAG优化，最后在ModelSim仿真平台上，用Verilog语言实现该算法，并进行了仿真结果分析和工作量分析。RAG优化后减少了加法器数量，降低了路径延迟。

　　关键词：DFT；余数系统；FIR；优化；Modelsim

　　0引言

　余数系统（Residue Number System, RNS）将传统的二进制数值表征系统中多位宽运算转换成多个并行且独立的短位宽运算，能够提高运算速度以及降低运算单元的功耗，从而提升并行处理单元的性能。离散傅里叶变换（Discrete Fourier Transform, DFT）是一种应用极为广泛的信号处理方法，与RNS相结合，因其成本和速度上的优势，在大量乘加运算的数字信号处理系统中得到广泛应用和研究。当前可编程数字信号处理（Programmable Digital Signal Processing, PDSP）和特定用途集成电路 (Application Specific Integrated Circuit, ASIC)的构建，正处于革命性的数字信号处理技术的前沿，在更多系统前端（如传感器、滤波器的应用等）正在逐渐替代DSP［1］。DFT在可编程器件上的快速实现算法和结构值得深入研究。

1循环卷积DFT算法

　　1.1余数系统

　　余数系统（Residue Number System，RNS）是一种古老的非权重数值表征系统，基于RNS可以实现加法、减法、乘法等整数运算。在相对素数的正整数基{m1，m2，…，mL}下定义动态范围M，M=Ll=1ml，在这个同构计算环内，定义：ZMZm1×Zm2×…×ZmL，其中ZM=Z/(M)与整数模M的计算环相关，被称为余数类模mod M［2］。通过xl=X mod ml定义数组X（x1，x2，…,xL），其中l=1,2,…,L，这种模映射可实现代数运算。

　　1.2DFT算法

　　素数因子循环卷积DFT算法也叫Rader算法［3］，定义素数长度N的DFT如下：

　　其直流组成部分：X［0］=∑N－1n=0x［n］。由于N是素数，根据数论变换理论可知：存在一个本原元素，一个生成元g，也就是a=gαmodp，该公式可以生成Zp域内除零之外的所有元素即(Zp/{0})，即在Zp/{0}中的整数a和Zp-1域中的指数之间存在一一对应的映射［4］。通过一个本原元素和一个生成元g产生元素n和k，用gn模N映射n，得到以下的模映射：

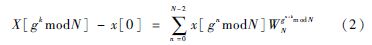
　　其中k∈{1,2,3,…,N－1}。

　　可以看到该式的右侧是一个循环卷积，即：

　　1.3FIR滤波器图解

　　有限常系数的FIR滤波器是一种线性时间不变（Linear Time Invariant，LTI）数字滤波器［5］。N阶FIR的输出对应于输入时间序列x［n］，是一种有限卷积形式，具体形式如下：

　　y［n］=x［n］f［n］=∑L－1k=0x［k］f［n－k］(7)

　　直接FIR滤波器是一种“抽头延迟”结构，由加法器和乘法器的集合构成。每个乘法器的操作数就是一个FIR系数，也称作“抽头权重”。循环卷积DFT与FIR滤波器是等价的，图1给出了式(6)相应的采用FIR滤波器的图形化解释。其中系数Wk5是复数，8位量化值如表1所示。　

　　在独立系数直接形式的模型中，通常把常数系数乘法器所需加法器的数量称为成本，图1的成本为22。这种直接形式的FIR体系仅在自适应滤波器等少数场合，通过DSP的RSIC结构的硬件开发 ［6］。通过系数的RAG优化，可以降低硬件成本，构造更为有效的PDSP实现。

2算法的优化与仿真

　　2.1系数的RAG优化

　　基于系统的转置结构，有WkN=WN－kN，k∈［1,N－12］。表1中的系数具有对称性，经非负化处理，需要实现的系数为：{256,79,243,207,150}，可见工作量可以降低一半。

　　乘法器-加法器图（MAG）技术是将系数拆分成几个因子，再通过几条路径来组合这些不同的因子，Dempster等人给出了所有合成成本为1～4个加法器的所有系数的可能配置， 系数的MAG图成本为{0,2,3,3,3}，共11个加法器。最优简化加法器图（RAG）能够进一步降低总工作量。Dempster和Macleod首先提出的RAG算法规则［7］如下：

　　(1)去除系数的符号，因为符号可以通过滤波器的抽头延迟线上的减法来实现；

　　(2)输入集合中2的幂的值通过硬连线的数据移位来实现，可以直接去除；

　　(3)创建一个能用一个加法器构造的系数的图集；

　　(4)用已知图集构造更高值的乘法器；

　　(5)必要时添加最小非输出基数（NOF）作为辅助系数。

　　根据此原则，RAG算法优化措施如表2。表2RAG优化措施需要实现的系数措施256, 79,243,207,15028，26+15，24×15+3，26×3+15，2×7515,3,7524-1,22-1，79-4

　　此时加法器的数量可降低到最小值6，所有的系数都是由3个加法器和3个减法器实现的。加法器路径延迟也从3降低到2。图2给出了最终的已简化的加法器图。

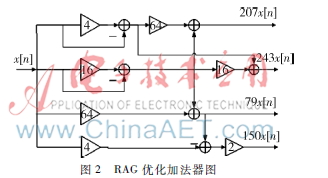
　　2.2ModelSim仿真

　　采用Verilog语言，运用转置FIR滤波器结构共4个进程来实现以上设计［8］。“STAGES”进程是一个区分3个状态：START、LEAD和RUN的状态机。“STRUCTURE”进程则定义了两个FIR滤波器通路，分别计算实部和虚部。“COEFF”进程为乘法器系数模块，而“RAG”进程实现优化的NOF因子。在Mentor公司的HDL语言仿真平台ModelSim上进行仿真，可以看到，输入信号序列x(n)=(10, 20, 30, 40, 50) ，y_real 和 y_imag 分别为X(k)的实部和虚部，由仿真结果可得X(k)=(-25+j34,-25+j8,-25-j9,-25-j35,150)，与手工计算所得结果完全一致。循环卷积DFT的Verilog仿真结果如图3。

3结论

　　利用RNS可将DFT的输入和输出序列重新排序， DFT运算转换成循环卷积算法，再用数论变换来计算卷积，采用RAG优化了系数，当N（滤波器阶数）为5时，所用加法器数量与直接FIR体系相比减少了73%；与MAG图相比减少了45% 。特别对于高阶滤波器，因为RAG通过已合成的系数生成了高密度小系数栅格，只要用很少的代价就可以实现新系数，工作量趋向于N，大大减少了加法器数量，降低了路径延迟。该算法的缺陷是要求N-1为高复合数，而N又是素数，因此可供选择的N只有费马数22t+1（t=1,2, 3, 4），长度很有限［9］，对较长序列则需分解为多维短序列来计算。

　　参考文献

　　［1］ 马上.基于余数系统的数字信号处理VLSI实现关键技术研究［D］.成都：电子科技大学, 2009.

　　［2］ 裴定一,祝跃飞.算法数论［M］.北京:科学出版社, 2002.

　　［3］ RADER C M. Discrete Fouriertransform when the number of data sample is prime［J］.Proc IEEE, 1968, 56(6):11071108.［4］ LIU Y, LAI EMK. Design and implementation of an RNS based 2D DWT processor［J］. IEEE Transaction on Consumer Electronics,2004, 50(1):376385.

　　［5］ 郝小江,黄昆.FIR数字滤波器设计及其FPGA实现［J］.微型机与应用,2013,32(19):2224,28.

　　［6］ 马维华,谢虎城,梁赫西，等.基于FPGA的FIR滤波器设计与实现［J］.微型机与应用,2013,32(23):1315,19.

　　［7］ Uwe MeyerBaese. 数字信号处理的FPGA实现［M］.刘凌，译.北京:清华大学出版社, 2003.

　　［8］ 吕晨阳,王建.基于System Generator的Rife算法的FPGA实现［J］.电子技术应用,2014,40(4): 4244.

　　［9］ 刘昌进.基于数论变换的运动估计算法研究［D］.合肥：中国科学技术大学,2005.