肖健，邵翠兰

　　（广东科技学院，广东 东莞 523083）

　　摘要： 在信息论中，数据压缩是数据处理的难题之一，尤其是图像无损压缩。JPEG－LS算法是公认的灰度图像有效的压缩算法。然而，对于计算机绘制的灰度图像（如CAD、SOLIDWORK等），其压缩效率低，限制了JPEG－LS的广泛应用。提出一种基于两步编码法的图像有效压缩算法，即建模和编码,算法与JPEG-LS灰度图像压缩标准进行对比实验，实验结果证明该算法提高了压缩效率。

　　关键词： 图像压缩；低熵源；预测误差；图像编码；冗余度

0引言

　　数据压缩是信息论的难题之一，解决方案有若干种［1］，预测误差编码是图像无损压缩最常见的算法之一，基于这种思想算法总体方案可分为两步：建模和编码。使用类图像的模型，从上一数据预测该点的强度来计算有效图像数据估计值。编码步骤包括计算预测误差，即实现与预测的强度差，压缩采用二进制表示。图像压缩方案首先使用日落算法实现［2］，算法有多种变形，如单通道，其预测误差和编码一次完成；双通道变型，先计算所有误差，再进行编码［3］。对于灰度图像，在算法复杂性和压缩效率比率最佳方案公认为是JPEGLS无损压缩标准［4］。基于JPEGS标准算法进行预测当前点的强度，当前点k是连续邻接点，用k比特数表示（称为上下文），当前点的强度、编码的预测和编码的整个过程可以分为三步［56］：

　　（1）计算当前点的上下文，引用上一强度值（x）；

　　（2）当前点强度值（）的预测源于上的值；

　　（3）ε=－x为计算预测误差的概率模型参数，使用步骤（1）和（2）及误差编码得到的数据。设误差ε是两边几何分布［56］，关于某个对称值呈现指数衰减分布，概率模型分别用上下文表示，分布对称中心可以移动使它接近于0［7］。

　　p(ε)=C(θ,d)θ|ε+d|（1）

　　当ε＝0，±1，±2…是预测误差时，参数取值范围0<θ<1，0≤d≤1/2，其特征分布对称中心C（θ，d）归一化因子由式（2）给出：

　　灰度图像JPEG－LS压缩算法优于其他算法，然而对于计算绘制的灰度图像，JPEG－LS算法效率低，限制了JPEG－LS的广泛应用。对于计算绘制的图像，值为0时预测误差ε的概率显著高于照片图像。ε使用RiceGolomb编码对字符编码［8］。在计算绘制图像的情况下，其中一串零的概率足够大，低熵源编码算法是有效解决此类型图像的方案。

　　编码低熵源算法已得到证明［8］，它提供任意预定的冗余，同时保留编码器和解码器中一般方法相同的存储器，算法的编码和解码率显著提高［910］。

1预测误差有效编码算法

　　预测误差构造一个高效编码算法，由一个低熵源贝努利源Sε与预测误差值的字母表生成字符序列Aε={ε|ε∈［－n,n］}，概率分布P(ε)由式（3）给出：

　　P(ε)=(1－θ)θε2θ,ε≠0;P(0)=1－θ（3）

　　式（3）是由式（1）和式（2）概率分布产生，令d=12（当d=0和d=12时，式（1）概率分布中心点为0［7］）。考虑以上情况，实际上ε+dd，即令|ε+d|≈|ε|。

　　设

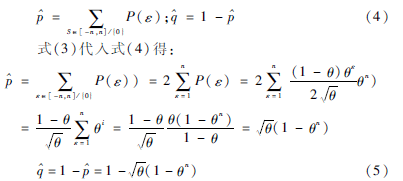
　　预测误差ε序列编码分为两步骤：第1步，一个简单的代码压缩源生成消息，且作为结果输出序列编码在第2步中使用一个更复杂的代码编码。源是一个低熵源，在第1步之后，输入序列长度明显减少，提供原始消息字符编码的总时间减小。第2步，使用目前已知算法中最有效的算术编码。考虑编码的第1步，字符输入序列划分成长度l=1/块（子字符串），其中由式（4）给出。如果一个块的误差值仅有零值，则这个块的编码为0，如果一个块包含误差值至少有一个非零值（用k表示，－1≤|k|≤n），则该码字长度等于l+1：这个块的开头码字为某个特殊字符k，后跟相同块长度l。在这种情况下，第l+1在开头的码字加字符k是有必要的，这表明在位于k后面长度l块中不可能是字符表观。

　　例如，设A={0，1，2}，P（0）=6/7，P（1）=2/21，P（2）=1/21，预测误差序列的编码为000000000001000 102000。

　　由式（4）得出=1/7,l=3的结果，编码序列形式 000 1001 0 21020第1步编码后得到序列，在编码第1步之后，令z1z2…zs。(zi∈A,A={k|－n≤k≤n})。

　　第2步编码是编码算法，在序列z1z2…zs选择长度为l的块后跟随任意特殊字符k，特殊字符0和k不包含在块中，序列z1z2…zs表示成：

　　0…0kz1…zll0…0kz′1…z′ll编码方案描述如下：

　　特殊字符0和k（－n≤k≤n）由编码器k0分别用l和1－l概率编码，在式（4）中定义。

　　考虑长度为l的块z1z2…zs内字符编码，令z1…zi－1=0…0i－1(i=1,2,…,l),判断字符zi的概率，位于第i个位置后i-1字符0的表观，则有:

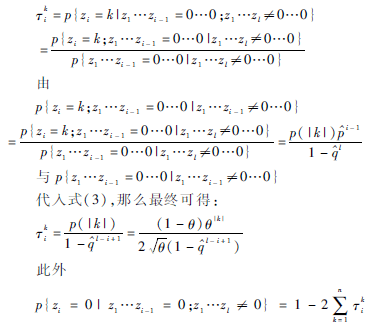
　　因此，块z1…zl中，在第i位置字符zi之后出现i-1个零表观，由编码器Ki用概率Γki编码，因为字符K和1－2∑nk=1Γki为零。最后，块中z1…zl字符位于任意字符k之后，由编码器k^以初始概率和p(|k|)分别为0和k编码［12］，其中p(|k|)由式（3）给出。概率Γki不存储在编码器和解码器之中，而是采用递归计算［1112］。首先，z1分别用字符0与k以Γk1和1－2∑nk=1τk1概率编码，当z1=k时,则所有的字符接字符k以编码器k^用初始概率p(|k|)和分别以k和0编码。否则，计算Γk2，字符z2用Γk2和1－2∑nk=1τk2概率分别以k与0编码［13］。因此，块z1…zl中的字符编码分为两步执行。

　　(1)计算Γki，字符zi用Γki和1－2∑nk=1τki概率编码。

　　(2)如果zi=k，则所有的字符接zi以概率和p(|k|)编码;否则，算法前移下一字符并返回到步骤（1）［1416］。

　　用递推公式Γki计算：

　　下一块的字符用相同方式编码，编码每一新块之前用初始数据进行更新。

　　使用之前步骤序列，考虑下面的编码结构。令：

　　p(0)==6/7

　　p(1)=2/21,p(2)=1/21,=1/7,l=3

　　编码序列为：

　　这个序列表示为：

　　特殊字符使用编码器k0用以下概率编码

　　p(z1)=p(z2)=p(z3)=p(z8)=p(z13)=(6/7)3=216/343

　　p(z4)=p(z9)=1－(6/7)3=127/343

　　第1块z5z6z7的字符串编码如下。由式（6）可得：

　　所以，z7=1，由编码器k3以τ13=2/3概率编码。第2块z10z11z12的字符串以相同的方式编码。因为(τ11)－1=38198，z10=1也遵循编码器k1以τ11=98/381概率编码，余下的字符串z11和z12由编码器k^以概率p(z11)=p(0)=6/7和p(z12)=p(2)=1/21编码。编码器与解码器存储大小以及所提出方法的编码与解码比率的特点在定理1中来描述［17］。

　　定理1设有一低熵源贝努利Sε，用字母表Aε={ε|ε［－n,n］}生成预测误差序列，以概率分布p(ε)由式（3）和一些r(0<r<1)给出。第(1)步，令这个源用上述l=1/(<1/2)进行编码，其由式（4）给出。第(2)步，冗余r=r/2，总的冗余不超过r,并且编码器与解码器V(Sε)总的存储器大小和一个符号T(Sε)编码与解码平均时间满足不等式:

　　V<C1log1,T<C2·log(1r）·loglog(1r）·logloglog(1r）+C3

　　其中C1、C2和C3为常数。

　　证明：总编码冗余量R=l′T。

　　l′=l1/l编码是第1步之后获得的代码平均长度（每个字符），当仅有字符0组成的块出现，概率可表示为l=(1－）l，因此有:

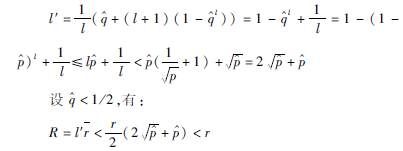
　　即总冗余量不超过r。对该方法的平均编码和解码时间进行评估，第（1）步序列字符压缩编码花费时间等于

　　因此，计算量的时间Γki用在第（2）步不超过

　　乘以平均代码长度l′得第（2）步编码的总时间，考虑第（1）步的时间等于0(1)，发现对于所提出的方法，一个字符编码和解码平均时间满足下式：

2算法实验结果

　　定理1给出了该方法有效性总体思想，然而更加实际意义是如何使所提出的方法对真实数据影响的问题。用Waterloo Repertoire GreySet1标准图像集对算法的性能进行测试实验,所有图像尺寸为256×256像素，测试使用联想PC的配置如下：CPU为IntelPentium(R) Dual-core,主频为2 GHz，内存2 GB，操作系统Windows 7。用JPEGLS标准对两种算法进行比较。表1和表2是两种算法比较结果，图像压缩k（bit）和时间t（s）的程度要求编码器来压缩图像，在这种情况下压缩程度是指对应于原图像（未压缩）中的一个字节（8 bit）的压缩文件中的比特数。换言之，如果L是原始文件的大小，L1是压缩文件的大小，那么压缩程度为8（L1/L）。一组计算机绘制图像压缩结果在表1中列出，另一组照片图像压缩数据在表2中列出。

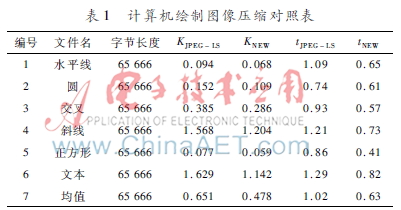
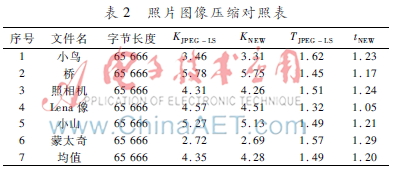
　　表1表明，计算机绘制图像压缩程度平均大于JPEGLS算法27%，编码率提高约37%。对于照片图像（如表2所示），新算法平均提高约2%，与JPEGLS算法相比，编码率仍然较高，提高约21%。实验结果表明，算法提供了良好的压缩比，证明所提出的算法是高效的。

3结论

　　本文所提出的基于两步编码有效算法经实验证明，计算机绘制图像编码的压缩比和编码率明显增加，分别提高27%和37%，超过JPEG算法。可应用于地图、地球表面的卫星图像和网页图形等实际领域。对于固定位置和固定数目的像素进行预测公式较简单，预测的像素点能充分利用。

参考文献

　　［1］ TROFIMOV V K. Efficiency of outputuniform coding of bernoulli sources for unknown message statistics［J］. Avtometriya， 2010,46(6)：3239.

　　［2］ TODD S, LANGDON G. G, RISSANEN J. Parameter reduction and context selection for compression of the grayscale images［J］. IBM J. Res. Develop， 2013,29(2):188193.

　　［3］ HOWARD P G, VITTER J S. Fast and efficient lossless image compression［C］. In Proc. IEEE Data Compression Conference, Snowbird, Utah, 2012: 351360.

　　［4］ WEINBERGER M J, SEROUSSI G, SAPIRO G. The LOCOI lossless image compression algorithm: principles and standardization into JPEGLS［J］. IEEE Transacation on Image Process, 2013,9(8):13101324.

　　［5］ NETRAVALI A, LIMB J O. Picture coding: a review［J］. Proceedings of the IEEE 1980,68(3): 366406.

　　［6］ REININGER R C, GIBSON J D. Distributions of the twodimentional DCT coefficients for images［J］. IEEE Transacations on Communicatons, 2013,31(6):835839.

　　［7］ MERHAV N, SEROUSSI G, WEINBERGER M J. Optimal prefix codes for sources with twosided geometric distributions［J］. IEEE Transacations on Information Theory, 2013,46(1):121135.

　　［8］ RYABKO B J, SHAROVA M P. Fast coding of lowentropy sources［J］. Probl. Peredachi Information, 2010,35(1): 4961.

　　［9］ RYABKO YA B, FIONOV A N. Homophonic coding with logarithmic memory size［M］. In Algorithms and Computation, Springer, Berlin, 2009:253262.

　　［10］ WITTEN I H, NEAL R M, CLEARY J G. Arithmetic coding for data compression communication［J］. ACM, 1987,30(6):520540.

　　［11］Library of images for testing and demonstration of data compression algorithms［EB/OL］.［20120112］（20160105）. http://cdb.paradiceinsight.us/corpora/Corpus% 20Waterloo/GreySet1/?C= N;O=A.

　　［12］ 王凤, 万智萍. 基于阈值与人眼特性的小波图像压缩算法［J］. 图学学报, 2013,34(6): 8086.

　　［13］ 褚静, 徐安成, 张美凤. 基于DWTLSSVM的图像压缩算法［J］. 计算机工程与应用, 2013,40(14):156159.

　　［14］ 杨晓,刘俊杰, 杨学友.基于ROI编码的任意尺寸测量图像的压缩方法［J］. 计算机工程与应用,2013,40(4): 1417.

　　［15］ 阳婷,官洪运,章文康,等. 基于小波变换的图像压缩算法的改进［J］. 计算机与现代化, 2014,40(10):123126.

　　［16］ 田驰.小波Contourlet变换图像压缩算法［J］. 长春工业大学学报(自然科学版) , 2014,40(4):8991.

　　［17］ 陈鸿,柏森,刘博文.混沌和小波变换的图像加密压缩算法［J］. 重庆大学学报, 2014,40(6):6570.