程政，陈贤富

　　(中国科学技术大学 信息科学技术学院，安徽 合肥 230027)

       摘要：短时交通流的准确高效预测对于智能交通系统的应用十分关键，但较强的非线性和噪声干扰使其对模型的灵活性要求较高,并且还需在尽可能短的时间内处理大量的数据。因此，讨论了用随机森林模型对短时交通流进行预测，该模型具有比单棵树更强的泛化能力，参数调节方便，计算高效，且稳定性好。观察交通流数据在较长时间跨度上的变化后，提取出主要特征变量构造输入空间，对模型进行训练后，在测试集上的预测准确率约为94%。与目前广泛使用的支持向量机模型进行对比分析，结果显示随机森林预测不仅准确率稍好于支持向量机，而且在效率、易用性及未来应用的扩展上都要优于支持向量机。

　　关键词：智能交通；交通流预测；决策树；随机森林；支持向量机

0引言

　　现代城市车辆增长的速率远大于新修道路的里程数，由此引发的道路拥堵、环境污染等一系列问题给人们的生活带来了很大不便。解决该问题的最好办法是发展智能交通系统（Intelligent Traffic System,ITS），利用交通诱导技术，提高交通路网通行效率。这要根据当前及未来时间内道路网的交通状态来为车辆建议较佳的行车路线，从而使车流均衡地分布于路网，发挥各条道路的最大功用。

　　反映路网状态的一个重要变量是交通流，即一定时间段内通过某一道路截面的车辆数。优秀的交通诱导系统需要根据在未来短时间（5~15 min）内的道路交通流作出诱导建议，而由于短时交通流数据的非线性和噪声干扰，使其规律很难把握，对于短时交通流的预测一直是个难点。

　　早期的预测模型主要有历史平均、线性回归、时间序列等，但预测精度不高，模型适应性不强。近些年研究较多的模型有交通仿真、混沌理论、神经网络和支持向量机（Support Vector Machine,SVM）［1］。机器学习方法由于有较强的理论框架，预测效果好，越来越成为受欢迎的参考模型。参考文献［2］总结了较多的研究和文献，表明神经网络有较好的预测效果，神经网络一度成为研究的热点。SVM有比神经网络更好的泛化（generalization）性能，也比神经网络更容易优化和求解，因此SVM也成为目前预测交通流较流行的一种方法［3］。

　　但影响SVM［4］性能的超参（hyper parameter）一直没有很好的确定方法，常用网格搜索（grid search）和随机搜索（randomize search）结合交叉验证（cross validation）。多数论文也探讨了利用进化算法对参数寻优，但这些不仅增加了模型的复杂度，还耗费了额外的计算时间。

　　因此，本文提出用随机森林模型来预测短时交通流，该方法对超参的调节要求不高，使用方便，与SVM相比，预测精度相近，但模型的训练时间却减少很多，并且适合运行在大规模的数据集上。

1随机森林算法

　　1.1算法步骤

　　随机森林［5］算法是BREIMAN L提出的一种集合多棵分类回归树（Classification And Regression Tree, CART）进行投票决策的方法。这是Bagging的思想，将多个弱学习器集合起来得到一个强的学习器。由于交通流预测的输出为实数，因此本文仅讨论了随机森林的回归算法，该算法如下：

　　（1） For r=1 to R，R为设定的随机森林中生成决策树的棵数:

　　①从总的训练集S中用bootstrap方法抽取一个大小为N的训练子集Sr；

　　②在Sr中重复以下步骤，直到节点的样本数不超过设定的最小值Lmtn,得到一个树Tr。

　　a.在n个特征变量中随机选择m个特征变量；

　　b.从m个特征变量中选择最佳的变量j和切分点s得到θr(j,s)；

　　c.将该节点依θr(j,s)切分成两个孩子节点。

　　（2）输出所有生成的决策树集合{Tr}R1，构成随机森林，模型的（回归）输出如式（1）所示。

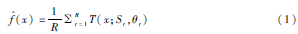
　　1.2完全生成树算法分析

　　以上步骤b中最佳的特征变量j和切分点s的选择需满足如下约束条件［6］：

　　其中,x(i)表示第i个样本值，y(i)表示对应的第i个输出值，P1（j,s）和P2(j,s)为分割后得到的两个子叶，c1和c2为这两个子叶的输出值。

　　式(2)中括号里的两项可通过各自求导解得：

　　c＾1=ave(y(i)|x(i)∈P1(j,s))

　　c＾2=ave(y(i)|x(i)∈P2(j,s))

　　外层的minj,s可通过扫描所有m个特征变量的值来确定，当特征变量含v个有序值时，共有(v-1)种二分方法，当特征变量含v个无序值时，共有(2v-1)种二分方法。又由于无序值一般用以表示类别，而类别个数一般不多，为保证随机森林中树之间的独立性，m的取值也不大，因此这样的穷举扫描能很快完成。决策树的这种特性也使其能很容易地处理有序和无序变量相混合的问题。如在本文中所讨论的问题既包含了车流量大小，也可以包含星期、天气等类别。

　　决策树可以完全生长来拟合复杂的数据变化，从而具有很低的偏差（bias）和很高的方差(variance)，不过对于训练集中微小的变动，在某一节点上产生不同分枝并逐层向下传播，可能产生相差很大的两棵树。普通的决策树模型一般都要进行剪枝（pruning）后才能有较好的泛化性能，否则很容易发生过拟合（overfitting），但是修剪的程度不好确定。同时决策树的生长方式会对假设空间造成搜索偏置，使得无法保证找到一棵全局最优决策树。所以，决策树生长方式相对简单，拟合能力强，但不容易得到很好的泛化性能。

　　1.3随机森林算法分析

　　随机森林算法是从总样本集中用bootstrap方法抽取一个子集来训练决策树，因此可认为每一棵树服从同一分布，则随机森林中树的平均输出的期望E(1RRr=1Tr)等于每棵树的期望E(Tr)。这即说明随机森林与单棵树有同样的偏差，其泛化性能的提高需要通过减少方差来实现，即平均许多带噪声的近似无偏模型来减少它们的方差［7］。

　　设树的方差D(Ti)=σ2，并且任意两棵树具有正的相关系数ρ，则输出均值的方差为：

　　D(1RRr-1Tr)=ρσ2+1-ρRσ2(3)

　　由(3)式可看出，当树的数量R很大时，右侧第二项将接近于零，但第一项将保持不变。在生成树的过程中，每一个节点分裂成两个分枝之前，都随机选取m≤n个输入特征向量来供分枝算法使用，这将使得每棵树之间的相关系数ρ减小，并且当减小m时也会减小ρ,由式(3)综上可知,即减小了输出均值的方差。但同时需要注意的是，当m减小时，决策树能获得样本的数据减少，偏差将增大，从而使得随机森林的偏差也增大。对于回归问题，BREIMAN L建议m的值取为n/3」，最小节点样本数lmin=5，但还是要依据实际问题对这些超参进行调节。

　　由于使用bootstrap抽样，故总样本集S中会留有一部分未使用的数据（Out of Bag, OOB），可以作为模型预测效果的验证，而不需要使用交叉验证的方式，这也提高了参数的调节效率。

2构造特征向量

　　本文采用了加利福利亚州交通管理局的PEMS网站的公开数据进行研究，数据来源于铺设于道路下面的线圈传感器采集的车流量数据，传感器全天候工作，每隔30 s报送一次数据，经累积后成为5 min时间段数据。　

　　图1是一周的车流量变化曲线。通过对数据集的大致观察可以发现，车流量在每24小时和每周均有一定的相似波动，但短时间内却很不规则。

　　所以要对路段未来时刻的车流量进行预测，需要加入时刻和星期作为特征变量，以及之前紧邻时间段的车流量数据。设路段某一时刻的车流量为flow(t)，则可构造输入空间特征向量为:x0=weekday，x1=t，x2=flow(t)，x3=flow(t-1)，x4=flow(t-2)， x5=flow(t-3)。对应输出为当前时刻后一时间间隔单位的车流量y=flow(t+1)。其中t为间隔时间，可取5 min、10 min、15 min。对数据进行清洗、整合后［8］,取8周的数据作为训练集，一周的数据作为测试集。

3实验分析

　　由于随机森林经常被作为无需调节参数的模型直接使用，本文首先采用默认值100棵树，分枝特征数为2，最小节点样本数为5作为模型的超参。硬件平台为Intel双核T6500处理器，3 GB内存的计算机，输入整理好的某一监测点的训练数据，运行2.6 s后得到针对该路段的5 min短时交通流预测模型。

　　对模型输入测试数据后得到的预测结果如图2所示。其中图2(a)为取测试集中某一天实际观测值和模型预测输出值在相同时刻叠加，可看出在短时间内交通流出现了频繁的变化，但模型预测输出能很好地跟随实际数据。图2(b)将一周的车流量数据的观测值和预测值分别作为x、y坐标值绘制，其中绝大部分点均聚集在y=x直线上，这反映了在整个测试集上模型对实际数据也具有很好的拟合性能。

　　本文采用如下指标来评估模型的表现：

　　（1）均方根误差（Root Mean Square Error）

　　表1所示为预测结果指标，可看出OOB集的指标能很好地反映模型的实际表现，故可用来评估模型。模型的预测准确率达到94%，这已可以满足工程实践的需求。

　　图3所示是将超参m分别取1~6构建模型，为得到光滑真实的曲线变化，将每个模型重复50遍后，得到其在各个样本集上的平均表现与波动。当m减小时，训练集上的误差将增大，而测试集上的误差先减小后增大，在m=2时测试集上的误差最小，这说明当m取较大时，出

　　现了过拟合，而当m取得太小时，又会有欠拟合出现。由于随机森林是以一部分偏差的增大作为代价来降低模型的方差，这就需要调节m来找到最小的代价实现最佳的预测输出。但从OOB和测试集上的误差变化来看，超参m对于模型预测性能的影响有限，同时超参的取值范围明确，所以模型对于参数调节的要求并不高。

4与SVM模型比较

　　在交通流预测问题上，SVM已被较多文献证明具有优于其他多种模型的表现［910］，因此本文选用了应用较为广泛的嵌入RBF核函数的SVR作为对比，该模型中惩罚系数C、核参数γ、回归参数ε均需要调节，因此参数的寻优较复杂。并且SVR模型在训练之前还应对各特征变量作标准化处理。

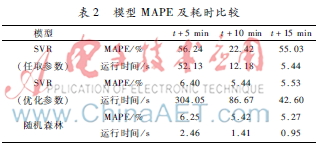
　　取5 min、10 min、15 min间隔的车流量进行预测，任选一组参数值的SVR模型和经随机搜索算法［11］得到的最优SVR模型、随森林模型作实验对比。从表2的实验结果可以看出，SVR的参数直接决定了模型的好坏，SVR模型的优化要耗费较多时间。并且，在相同数据集上，SVR的每一次训练时间可达随机森林的十多倍，当数据量增大时，差距将更大，这严重降低了模型在实时交通流预测问题中的实际应用价值。与此同时，随机森林的预测表现比SVR优化参数后的表现还要稍好一点。

5结论

　　对于短时交通流预测问题，与人工神经网络和SVM相比，随机森林参数调节方便，模型训练时间短，同时还有较好的预测精度。在输入特征变量处理上，其内部的决策树模型能很好地适应连续和离散变量，还能容忍小部分数据的缺失。并且，在实际应用中，需要监控的是整个路网的状态，输入变量可能会涵盖更多相邻道路数据，为了提高预测精度，还需引入突发事故、道路施工、天气状况等特征变量，使得输入向量的维数很高，同时每

　　时每刻又有海量的交通数据可以回传用作模型的在线训练，随机森林的特性可以使其将高维向量分散到低维处理，又能够同时在不同的机器上单独生成树，从而能高效地建模求解。

参考文献

　　［1］ VLAHOGIANNI E I, KARLAFTIS M G, GOLIAS J C. Short-term traffic forecasting: where we are and where we’re going［J］. Transportation Research Part C Emerging Technologies,2014,43(1):319.

　　［2］ 王凡．基于支持向量机的交通流预测方法研究［D］．大连：大连理工大学，2010.

　　［3］ 陆海亭，张宁，黄卫，等．短时交通流预测方法研究进展［J］．交通运输工程与信息学报，2009,7(4):8491.

　　［4］ CHEN P H, LIN C J, SCHLKOPF B. A tutorial on νsupport vector machines［J］.AppliedStochastic Models in BusinessandIndustry,2005,21(2):111136.

　　［5］ BREIMAN L.Random forests［J］. Machine Learning,2001,45(1):532.

　　［6］ BREIMAN L, FRIEDMAN J, CHARLES J S, et al.Classification and Regression Trees［M］. US: Chapman and Hall, 1984.

　　［7］ HASTIE T, TIBSHIRANI R, FRIEDMAN J. The element of statistical learning: data mining, inference, and prediction. (2th ed)［M］.US: Springer, 2009.

　　［8］ MCKINNEY W. Python for data analysis［M］. US: O’Reilly, 2012.

　　［9］ 朱征宇，刘琳，崔明．一种结合SVM与卡尔曼滤波的短时交通流预测模型［J］．计算机科学，2013, 40(10): 248251.

　　［10］ 傅贵，韩国强，逯峰，等．基于支持向量机回归的短时交通流预测模型［J］．华南理工大学学报(自然科学版)，2013,41(9):7176.

　　［11］ BERGSTRA J, BENGIO Y. Random searchforhyperparameter optimization［J］.Journal of Machine Learning Research, 2012, 13(1): 281305.