0 引言

    近年来，随着微机电（MEMS）技术的快速发展，传感器的应用越来越广泛，传感器标定也越来越受到关注。传感器将某种物理量转化为便于利用的电信号，转化过程中每种传感器都有相对应的转化模型，模型中的各种参数都需要通过实验来事先确定，这一过程就是传感器的标定^[1]。标定是设计、制造和使用传感器的一个重要环节，任何传感器在制造、装配完毕后都必须进行标定，以保证量值的准确传递，并将标定数据作为改进传感器设计的重要依据^[2]。

    对于加速度计等振动传感器，传统的标定方法是利用可精确控制方位和转速的机械转台进行标定，其成本很高^[3]。文献[4-5]提出一种MEMS惯性传感器标定方法，成本与精度优于传统方法，但在标定数据处理方法上仍存在不足，不同的数据处理方法有不同的精度，对于一个精度不够高的传感器，若标定数据处理方法得当，会在实测中产生较小的误差，提高传感器精度。

    本文提出一种低成本的标定方法，在最小二乘估计的基础上建立了传感器的输入—输出特性及其误差关系。利用重力加速度作中间量，确定加速度计模型未知参数项，降低其不确定性，提高传感器精度^[6-7]。此方法为分析多传感器定位系统的标定提供了有效的研究工具。

1 传感器模型 

    本文提出的多传感器定位系统框图如图1所示。由于三轴加速度计传感器、陀螺仪与磁场传感器都将物理量分解到传感器的三个敏感轴上并转化为相应的电信号^[9]，因此传感器模型的形式相同。本文主要以加速度计的模型为例加以说明。

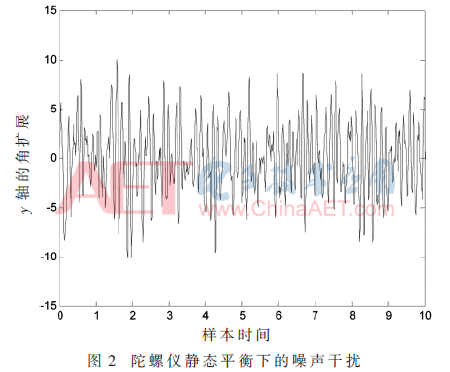
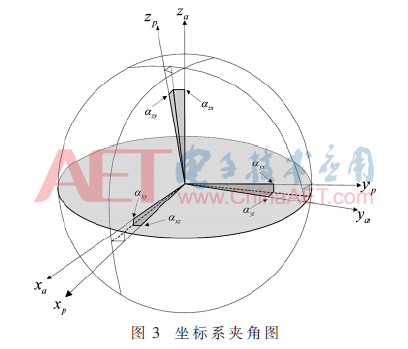
    系统中除上述转换误差以外，加速度计、陀螺仪等还存在电噪声的干扰，如图2所示。由于加速度计传感器装配误差的存在，使其三个敏感轴非严格正交。基于上述分析与假设，本文建立了一个多传感器标准平台，具备非正交性敏感轴以及非线性响应的特点，如图3所示。O-x_ay_az_a是空间中的一个正交坐标系，即加速度计坐标系；O-x_py_pz_p为传感坐标系，即由加速度计的敏感轴组成的非正交坐标系。标量α_ij为O-x_ay_az_a和O-x_py_pz_p之间的夹角，表示图中平台系统的第j个轴所对应的加速度计第i个敏感轴的相对方位角。a_p表示加速度计传感器将物理量分解到三个敏感轴上后实际承受的加速度大小，即为3×1的列向量。a_a表示加速度计的原始输出电压向量值，也为3×1的列向量。由系统输入输出间关系可得，以上两个加速度矢量之间的关系转换式如下所示： 

    假设由于装配问题产生的误差在一定的时间长度内保持为常数。于是可得，在敏感轴处测得的加速度与同一系统中其真正加速度计值之间的线性模型为： 

其中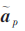，是由加速度计获得的测量值；K_p是一个3×3对角矩阵，其对角线上的元素表示加速度计每个敏感轴的比例因子及加速度计的单位输出电压对应的加速度大小；b_p是一个3×1的零偏列向量，表示加速度计每个敏感轴上的偏差信息，是在没有任何加速度输入情况下加速度计输出电压对应的加速度大小；n_p是3×1的噪声列向量，由各种非确定性因素产生的随机噪声，也可看作零偏漂移，反映传感器的输出随机特性。实际上，这些参数会随着传感器温度的变化而有所改变。本文假设温度在一定时间内恒定不变。考虑到实际的三轴加速度计的装配误差以及噪声干扰一般很小，此处忽略不计。将式(1)变换后带入式(2)，最终可确定加速度计模型为：

    当选取x_a轴和x_p轴重合，y_a在x_p和y_p决定的平面上垂直于x_p，z_a轴与x_a和y_a正交，那么实际的3×3 T矩阵就只有3个出自α_ij的未知角度^[10]。考虑到实际三轴加速度计很小的装配误差，对于加速度计坐标系与传感器坐标系之间的夹角α_ij，有sinα≈α，cosα≈1，再根据力的合成与分解，可以将式(3)中的加速度计模型简化为：

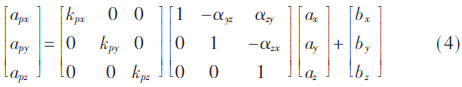
    在相同情况下，认为陀螺仪与加速度计的误差源相同^[11]，因此可建立与其同样的模型，代换相应的变量后可以表示为：

    式(3)所示的模型也同样适用于磁场传感器。

2 参数项的标定

    简单地说，本文对未知参数的确定性项进行标定问题就是在已建立的含有一组未知参数的加速度计模型基础上，通过标定分别获得这组数据的最优解。

    加速度计确定性项标定的任务是通过实验确定上节加速度计模型中的k_px、k_py、k_pz、α_zx、α_zy、α_yz、b_x、b_y、b_z这9个未知参数。传统的加速度计标定方法一般是利用高精度的机械转台来完成，但高精度的机械转台成本高，不适用于低成本MEMS加速度计的标定。此处用到的参数标定法不仅适用于三轴加速度计的标定，也适用三轴陀螺仪和三轴磁场传感器的标定。

    式(4)可以发现加速度计的输出涉及9个未知参数，因此需要记录加速度计在9个姿态下的输出，从而得到约束方程，求解此非线性方程即可得到所有的确定性项参数。为提高求解的准确性和精确度，一般记录会多于9个姿态，本文利用一种新方法获得确定性项参数的最优解。已知有参数矢量表达式：

其中：k_pi(i=1，2，3)是矩阵K_p的对角元素；b_i(i=1，2，3)是列向量b_p的元素；α_ij(i=1，2，3；j=1，2，3)是的矩阵T中的元素。

    本文标定建立了一个数据优化的准则，通过它来不断调节并最终确立系统上述未知参数的值。所选准则最大限度地减少了实际加速度与测量加速度之间的差异值^[12]。此问题的表达式可写为：

    在一个自由落体参考系中，常用加速度计来测量加速度，考虑到静止状态时，加速度计只受重力的作用，因此测量的加速度为地球引力常数（g=9.81 ms^-2），相应加速度计的输出是重力在各个敏感轴上的分解。此处规定其方向为一根线与一个悬挂重物构成的简易重力摆的线的反向。在这种情况下，需要建立一个精确的加速度表达式，其步骤包括测定加速度在不同方向的幅度大小，即可求解式(7)。

    本文提出了一种利用27个测量位置的求解方法，其具体步骤如下：

    (1)起始位置x轴指向“下”：9个测量值与两个转角相结合。首先，绕z轴分别旋转角度θ=0°、10°、20°、30°、45°；然后，将以上每个已定义的旋转角(θ=0°除外)绕x轴分别进行角度为Ψ=0°、-45°的两次旋转。表达式如下：

    为提高求解的准确性和精确度，文中将27个测量值设为分开的2组：14个用于优化和13个作为测试集。经过以上考虑，各参数所取的一组初值为：=[2.61，2.61，2.61，0，0，0，0，0，0]^T，变换不同姿态，采集加速度计的输出, 最终可以得到三轴加速度计的标定结果为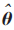：=[2.67，2.726，2.602，1.605，-1.79，-4.79，3.78×10^-4，4.62×10^-3，-6.81×10^-3]^T。对测试集进行研究与分析可以发现，其转角和偏移值均与数据手册相符合^[13]。

3 结果与分析

    实验针对无人自主航行器的导航定位，融合惯性和视觉传感器的运动估计，利用MATLAB进行仿真。

    针对加速度计模型中的确定性项标定分析，在每个姿态下的加速度计输出向量的大小分布情况如图4所示。从图4中可以直观地发现，经过加速度计标定，三轴加速度计输出向量的模值在标定中不断被优化，误差较小，为系统提供了更高精度的保证^[14]。

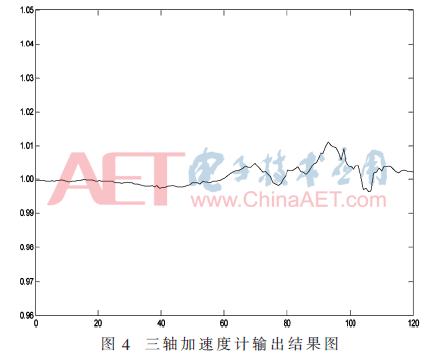
    此外，在确定性参数标定过程中，测试集的输出平均误差为-0.03 ms^-2，标准差为0.06 ms^-2。平均误差相对较小，大小仅为标准差的一半。因此可以得出结论：应用此方法进行确定性项中加速度计参数的标定可明显提高系统精度。

4 结语

    本文针对融合惯性和视觉以及磁场传感器的运动估计进行研究，提出了一种低成本高精度的标定方法。方法基于最小二乘估计并利用重力加速度最优化传感器各参数项，使得低成本传感器实测中的误差降低，从而提高系统传感器精度。实验结果分析表明，本文建模及标定方法的优势与有效性为无人自主航行器的导航定位系统的研究提供了有力的工具^[15]。

参考文献

[1] CHATFIELD A B.Fundamentals of high accuracy inertial navigation[J].Progress in Astronautics & Aeronautics，2013，6（1）：35-39.

[2] 张煌辉.基于视觉和惯性传感器的移动机器人自定位研究[D].北京：中国科学院研究生院，2012.

[3] DONOVAN G T.Position error correction for an autonomous underwater vehicle Inertial Navigation System(INS) using a particle filter[J].IEEE Journal of Oceanic Engineering，2012，37(3)：431-445.

[4] GLUECK M，OSHINUBI D，SCHOPP P，et al.Real-time autocalibration of MEMS accelerometers[J].IEEE Transactions on Instrumentation & Measurement，2014，63(1)：96-105.

[5] SKOG I，HANDEL P.Calibration of a MEMS inertial measurerment unit[C].XVII IMEKO World Congress Metrology for a Sustainable Development，Rio de Janeiro，Brazil，2006：17-22.

[6] BAEK S H，PARK J，KIM D M.Giant piezoelectricity on Si for hyper active MEMS[J].Science，2011，46(1)：27-41.

[7] FROSIO I，PEDERSINI F，BORGHESE N A.Autocalibration of triaxial MEMS accelerometers with automatic sensor model selection[J].Sensors Journal IEEE，2012，12(6)：2100-2108.

[8] ROBLA S，LLATA J R，Torre-Ferrero C，et al.Visual sensor fusion for active security in robotic industrial environments[J].Eurasip Journal on Advances in Signal Processing，2014(1)：1154-1165.

[9] PLACHT S，F?譈RSATTEL P，MENGUE E A，et al.ROCHADE：robust checkerboard advanced detection for camera calibration[M].Springer International Publishing，2014：766-779.

[10] 夏凌楠，张波，王营冠，等.基于惯性传感器和视觉里程计的机器人定位[J].仪器仪表学报，2013，34(1)：166-172.

[11] BRAS S，CUNHA R，VASCONCELOS J F，et al.Experimental evaluation of a nonlinear attitude observer based on image and inertial measurements[C].American Control Conference(ACC)，2010：4552-4557.

[12] PATERNAIN S，TAILANIAN M，CANETTI R.Calibration of an inertial measurement unit[C].Advanced Robotics (ICAR)，2013 16th International Conference on.IEEE，2013：1-6.

[13] Analog Derices.Adxl345 datasheet(2nd ed)[M].Norwood Massachusetts：Analog Devices，2011.

[14] 杜光勋，全权，蔡开元.视觉与惯性传感器融合的隐式卡尔曼滤波位置估计算法[J].控制理论与应用，2012，29(7)：833-840.

[15] CHEN J，YANG C J，HOFSCHULTE J，et al.A robust optical/inertial data fusion system for motion tracking of the robot manipulator[J].Journal of Zhejiang Universityence C，2014，15(7)：574-583.