刘 伟，杜 江

　　（成都信息工程大学 通信工程学院，四川 成都 610225）

　　摘要：在MIMO-OFDM无线通信系统中，常规的QRM-MLD检测算法的复杂度是固定的。为了降低算法的复杂度，基于传统的QRMMLD的树搜索思想，提出了一种改进的算法，该算法能根据星座点之间的相对距离以及在不同信道条件下接收符号在星座图中的位置差别，在保留的M个候选值中进一步减少候选点数。仿真结果表明，该算法能保证在误码率性能损失很小的情况下大大减少检测过程的访问节点数，降低了算法的平均复杂度。

　　关键词：多输入多输出；正交频分复用；QRM-MLD；球形译码；信号检测

0引言

　　在平坦衰落信道下，多输入多输出（MIMO）技术能给无线通信系统带来显著的容量提升，而正交频分复用（OFDM）技术能将一个宽带频率选择性衰落信道转变为若干个窄带平坦衰落子信道。因此结合二者技术优势的多输入多输出正交频分复用（MIMOOFDM）无线通信系统已成为新一代高速无线通信系统中的研究热点［12］。MIMO检测是MIMOOFDM系统接收端最复杂的任务，常见的信号检测算法有：复杂度低但检测性能不佳的线性检测方法，如迫零（Zero Forcing,ZF）算法［3］和最小均方误差（Minimum Mean Square Error,MMSE）算法［4］；理论上具有最优检测性能但复杂度过高的算法，如最大似然（Maximum Likelihood,ML）检测算法；具有次优检测性能的方法，如球形译码算法［1,5］。球形译码算法复杂度比ML算法大大降低，使其能在硬件上得以实现［2，68］。按照搜索策略的不同，可将球形译码的树搜索策略分为FinckePohst策略和SchnorrEuchner策略两类，也常称为深度优先树形检索和宽度优先树形搜索［9］。QRMMLD便是一种宽度优先的树搜索算法，由于在每层中仅保留M个度量值最小的向下层检索的节点，因此其复杂度是固定的并且只由M和树的层数决定［10］。

　　本文提出的改进算法能在保证误码率性能的前提下进一步减少每层中保留的节点数，大大降低了整个检测过程的平均复杂度。

1系统模型

　　考虑具有NT根发射天线和NR根接收天线的MIMOOFDM系统，其中NR ≥ NT，假设各子信道之间相互独立且为平坦衰落瑞利信道，则接收信号可表示为：

　　y=Hx+w (1)

　　其中，x=x1,x2,…,xNTT表示发送信号向量，ExxH=1/NTINT；y=y1,y2,…,yNRT表示接收信号向量；w=w1,w2,…,wNRT表示独立同分布的加性高斯白噪声向量，其方差为σ2w ，均值为0；H表示NT×NR维的信道矩阵。

　　假设接收端具有理想的信道状态信息，C表示星座集中星座点的个数，则最大似然解可表示为：

　　ML=argminx∈CNT‖y－Hx‖2(2)

　　其中，‖y－Hx‖是向量的欧式范数即度量值。对信道矩阵H做QR分解，即H=QR，并且左右两边同时乘以QH，则可得到：

　　=Rx+(3)

　　其中，=QHy，=QHw。由于Q为酉矩阵，不改变度量值大小；R为NT×NT维的上三角矩阵，则度量值可表示为：

　　‖y－Hx‖=‖QH（y－QRx）‖=‖－Rx‖(4)

2传统QRMMLD检测算法

　　QRMMLD检测算法的核心由两部分组成：M算法和QR分解。通过式（4）的变换可将全检索空间转换为一个有限制的树形搜索，最大似然解可变换为：

　　ML=arg minx∈CNT‖－Rx‖2(5)

　　令ri,j表示R中第i行第j列的元素，假设NT=NR=P,则度量值‖－Rx‖2可表示为：

　　其中，Ti为部分距离PD（Partial Distance）。那么最大似然解可理解为在P级树搜索中，使得P个部分距离之和最小的候选向量。图1为一个采用8PSK调制方式的3×3 MIMOOFDM系统的QRMMLD树搜索过程示意图，其中实线表示保留路径，虚线表示裁剪路径。

　　从图1可知，传统QRMMLD算法从根节点（第4层）开始，按照宽度优先的策略遍历树，每层仅保留M个最小PD值的节点，直到到达叶节点（第1层）时结束搜索过程，将具有最小部分距离之和的路径作为检测输出。

3改进的低复杂度检测算法

　　传统QRMMLD算法的复杂度主要体现在每层的部分距离PD的计算上，也即和M算法保留的节点个数与树的层数直接相关。本文提出的改进算法，对M个候选节点进一步添加限制条件：

　　T(c)i<d2(7)

　　其中，T(c)i表示每层C个部分距离中的任意一个；d2表示限制阈值，其与星座点之间的相对距离与M值有关。

　　假设满足式（7）的节点个数为K，通过合理地设置d2的大小，使得大多数情况下K≤M，从而达到降低复杂度的目的，如功率归一化的16QAM调制，M=5时该值可设为d2=0.4。然而在信道条件较差的情况下，接收符号将落在星座图区域的外部，可能导致不满足式（7）的候选点的存在，这时新的候选节点只保留一个最小值，即K=1。

4仿真分析

　　本节主要从复杂度和误码率性能两方面对新算法和传统算法做了仿真对比分析，仿真参数设置如下：天线配置为4×4；调制方式为16QAM；OFDM子载波数为64；循环前缀长度为16；信道编码采用1/2码率的卷积编码。

　　4.1复杂度分析

　　由于本文提出的新算法与传统的QRMMLD检测算法在搜索思路上基本一致，所不同的只是新算法将每层保留的节点数进一步减少，因此在进行算法复杂度比较时，仅考虑整个检测过程中需要计算部分距离的节点个数。图2为复杂度对比分析结果图，其中传统QRMMLD算法的M=5，新算法采用两种限制条件与传统算法作比较，分别为d2=0.4，d2=0.447 2。

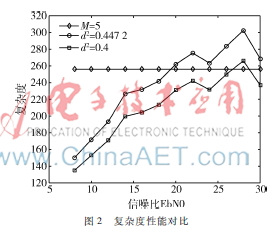
　　从图2可以看出，该仿真条件下，本文提出的算法检测过程的平均复杂度大大减少，经过计算分析可知，在两种限制条件下大致分别减少了27.04%和17.54%。新算法的复杂度随着信噪比的增加有渐增的趋势，并且可能大于传统算法，这是因为信道条件越好，接收符号落在星座图内部的概率越大，即在新算法限制条件下保留的节点数越多。但是当复杂度高于传统算法时，此时的误码率基本已经降至10-3以下，故并不影响新算法在减少复杂度上的优势。

　　4.2误码率性能仿真分析

　　本小节将检测算法中的ZF算法、MMSE算法、ML算法、传统的QRMMLD算法以及本文的新算法放在同一仿真环境下进行误码率性能比较，仿真结果如图3所示。

　　从图3可以看出，新算法在信噪比较低时的误码率可能会稍大于传统的算法，随着信噪比的增加，新算法提升误码率性能的效果逐步提升，在BER=10-3时，新算法的两种情况分别比传统算法提升了0.5 dB和0.7 dB，并且平均复杂度都有相应的降低。

5结论

　　本文基于传统的QRMMLD算法思想，提出了一种改图3误码率性能对比

　　进的低复杂度检测算法。通过复杂度分析和性能仿真分析，通过调整限制阈值的大小，该新算法能在复杂度和性能的表现上获得较好的折衷效果。

参考文献

　　［1］ 田木村, 宋婷, 刘江顺, 等. MIMOOFDM 系统中改进的格点减少检测算法［J］. 电子技术应用, 2014, 40(7): 109111.

　　［2］ 房汉林, 葛利嘉, 朱国庆. 2× 4 MIMOOFDM 系统中 KBest 检测器的设计与实现［J］. 电子技术应用, 2014, 40(11): 98101.

　　［3］ GOLDEN G D, FOSCHINI C J, VALENZUETA R A, et al. Detection algorithm and initial laboratory results using VBLAST spacetime communication architecture［J］. Electronics Letters, 1999, 35(1): 1416.

　　［4］ BURG A, HAENE S, PERELS D, et al. Algorithm and VLSI architecture for linear MMSE detection in MIMOOFDM systems［C］.Proceedings of 2006 IEEE International Symposium on Circuits and Systems, ISCAS 2006,2006.

　　［5］ LARSSON E G. MIMO detection methods: how they work［J］. Signal Processing Magazine, IEEE, 2009, 26(3): 9195.

　　［6］ HOCHWATD B M, BRINK S T. Achieving nearcapacity on a multipleantenna channel［J］. IEEE Transactions on Communications, 2003, 51(3): 389399.

　　［7］ CHAN A M, LEE I. A new reducedcomplexity sphere decoder for multiple antenna systems［C］. IEEE International Conference on Communications, ICC 2002, IEEE, 2002, 1: 460464.

　　［8］ 唐元元, 张德民, 刘哲哲, 等. TDLTE 系统中软输出球形译码检测算法研究［J］. 电子技术应用, 2012, 38(11): 5558.

　　［9］ CHIUEH T D, TSAI P Y, LAI I W. Baseband receiver design for wireless MIMOOFDM communications［M］. John Wiley & Sons, 2012.

　　［10］ 张朝霞, 王琼, 刘佳. 基于 QRM—MLD 的 MIMO 检测算法研究［J］. 通信技术, 2013 (10): 8790.