魏本刚，陈洪岗，李红雷，赵丹丹

　　（国网上海市电力公司电力科学研究院，上海200437）

　　摘  要： 变压器是电力系统中十分重要的设备，其热点温度是指导变压器负载运行方式和影响变压器绝缘寿命的重要参数，准确计算绕组热点温度具有重要意义。在分析变压器内部散热过程及其热特性行为的基础上，考虑日照、风速等环境因素对油浸式变压器的参数带来的影响，根据实验数据，利用神经网络进行建模预测，对网络的结构、算法的改进优化等问题进行了研究。通过与实际测量值和导则计算值相比较，结果表明，L-M算法优化的神经网络算法比导则算法更接近实际测量值。

　　关键词： 变压器；绕组热点温度；神经网络；油热特性参数；L-M算法

0 引言

　　电力变压器广泛应用于各个等级的电网中，对电能的经济传输、灵活分配和安全使用具有重要作用[1]。当前用电需求不断增多，电力变压器容量不断增大，但其几何尺寸并未因此增大，所以涡流损耗和杂散损耗会提高，引起绕组发热更多，增加了变压器故障的发生[2]。当前配电网中有75%左右是油浸式变压器，长期暴露在高温环境中，会使绝缘油纸板发生老化，造成变压器的寿命缩短[3]。根据6 ℃法则，油浸式变压器热点温度为98 ℃时其相对老化率为1，当热点温度高于98 ℃时，每升高6 K，其寿命降低一倍即老化率增加一倍[4]。所以准确确定变压器在不同负载与环境温度下的热点温度具有十分重要的意义。

　　目前最准确的测量热点温度的方法是直接测量法，即在变压器靠近导线位置预埋测温传感器，但在实际运行时直接测量成本较高，且运行维护困难，此方法主要是实验中使用[5-6]。工程上对于已经投运的变压器通常用间接方法得到绕组热点温度，比较常规的方法是IEEE Std C57.91导则[7]和IEC 60076导则[8]推荐的变压器绕组热点温度计算公式。推荐的计算公式忽略了环境因素，比如日照、风速等对顶层油温度和热点温度的动态影响，存在局限性。为此，国内外很多学者都在探寻计算顶层油温度和热点温度的新方法。文献[9]中指出了推荐计算公式的局限性，建立了变压器顶层油温度模型，采用后向欧拉离散公式、线性回归计算顶层油温度和辨识模型参数，但计算仍存在较大误差。文献[10]考虑油粘度和损耗随温度的变化，运用传热学理论将变压器内部传热过程等效为2个有串联关系的集总参数热路，研究得到顶层油时间常数小于IEC 60076导则推荐值，但模型简化时忽略了油与油箱之间的温度差和油箱外壁的复合换热过程。文献[11]运用热点类比、传热学理论在文献[10]基础上建立了基于热点温度与环境温度之差的热点温升简化模型，为简化计算模型，直接忽略了铁心损耗对整个模型的影响。文献[12]利用遗传算法优化变压器热特性参数并建立直接与环境条件、负载以及冷却系统状态等现场运行参数相联系的变压器温度动态计算模型，可以有效估算和预测热点温度以及变压器内部油温度，计算精度得到提高。文献[13]中对热点温度计算公式进行了改进，设定y=2x，几乎不影响温度计算结果的准确性，对于过载运行的变压器具有更准确的预测结果，提高了预测的安全性。

　　本文基于变压器热特性行为分析，考虑温度变化和环境因素对油热特性参数的影响，利用导则推荐的公式，选取对变压器热点温度影响比较大的参数。将导则实例数据作为数据库，利用L-M算法优化改进的神经网络进行训练，得到的网络可以预测出动态合理的油热特性参数。利用得到的合理参数，根据改进的热点温度计算公式进行计算，通过与实际测量值和导则计算值相比较，结果表明：改进的神经网络算法比导则算法更接近实际测量值。

　　1 绕组热点温度计算方法

　　在IEC 60076标准中，规定了油浸式变压器绕组热点温度计算方程：

　　当负载系数增大时，

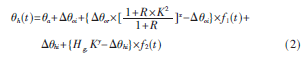
　　其中：

　　其中：

　　式(1)中，h为任意负载情况下热点温度，℃；a为环境温度，℃；o为顶层油温升，℃；h为热点温度对顶层油温的温升。式(2)中，oi为开始时的顶层油温升，℃；or为额定损耗下顶层油稳态温升，℃；R为额定电流下的负载损耗和空载损耗之比；K为负载系数，它是负载电流与额定电流之比；x为油的指数；y为绕组指数；hi为开始时热点温度对顶层油温的梯度。式(3)、(4)、(6)中，k11、k21、k22为热模型常数，o为平均油时间常数，绕组时间常数。

　　从导则推荐的方程可知，表示变压器运行时任一负载情况下的总损耗与额定情况下的总损耗之比，H为额定负载下热点对绕组顶部油的温差，Ky为任一负载情况对额定负载情况的温差系数。

2 变压器发热机理分析

　　运行中的变压器其内部部分电磁能量将转变为热量，在铁心、绕组等发热体中均要产生损耗，其中绕组的损耗是内部的主要热源，损耗将变为热量向外传递到周围介质中，引起变压器温度升高。

　　变压器的损耗表现为以下形式：

　　PT=PC+PL(7)

　　式(7)中，PT为总损耗，W；PC为空载损耗，W；PL为负载损耗，W。

　　空载损耗是变压器的一个绕组端子加额定电压，其他绕组开路所吸收的有功功率。空载损耗由涡流损耗和磁滞损耗构成。负载损耗由绕组导线中的电阻损耗、涡流损耗以及变压器夹件、油箱等结构中的杂散损耗构成。在变压器内部，铁心外包有套筒，将铁心油道与绕组油道隔开，所以负载损耗是造成绕组温度升高的最主要原因。

　　空载损耗可以表示为：

　　式(8)中，P1为铁心中的磁滞损耗，W；P2为铁心中的涡流损耗，W；h为磁滞损耗系数；e为涡流损耗系数；f为电流频率，Hz；Bm为磁通密度的最大值，Wb/m2。由式(8)可看出，空载损耗与磁通密度的最大值Bm的平方成正比。因为变压器铁心的磁化曲线具有饱和特性，通常变压器设计时将Bm值选择在磁化曲线的接近饱和区，所以当负载电流增大时，Bm随负载电流的增加并不大。

　　负载损耗可表示为：

　　PL=I2R+PE+PS(9)

　　式(9)中，I2R为绕组导体的直流电阻损耗，W；PE为绕组的涡流损耗，W；PS为金属部件的杂散损耗，W。

3 热点温度参数变量的确定

　　导则中给出了一个250 MVA、ONAF冷却方式的变压器实例，以此为基础，根据式（1）～式（6）得到单个参数变化对热点温度变化的影响，如表1。

　　由表1可知，有些参数对热点温度的影响甚微，比如顶层油初始温升Δθoi、负载损耗与空载损耗的比值R、初始时热点油温对顶层油温梯度Δθhi，因此可以忽略它们的影响。对热点温度影响比较大的是与油和绕组相关的参数，即油指数x、油时间常数o、绕组指数y、绕组时间常数，导则中给出了变压器热特性参数的推荐值，见表2。

　　热特性参数推荐值是根据经验给出的。但是对于实际运行来说，热特性参数特别是油的热特性参数，即油指数x、油时间常数o，受温度影响会有相对比较大的变化，所以获得准确的动态热特性参数对热点温度的精确预测具有重要意义。

　　实际情况中，可以得到的参数有环境温度、初始顶层油温升、负载损耗和空载损耗比、顶层油温度。所以要想得到准确的油热特性参数，只能依据这些参数来获得。公式（1）中，a+o即为环境温度与油箱内顶层油温升之和，得到的为顶层油温o。这样就将公式（2）和公式（5）中的热点温度与顶层油温相关的部分舍掉了，实际情况中得到的o为准确值，这样有利于得到比较准确的油热特性参数。

4 神经网络结构设计

　　BP神经网络通常由输入层、隐含层和输出层组成，层与层之间全互连，每层节点之间不互连。如图1所示。对应的网络输入X=[x1，x2，…，xn]T，输出Y=[y1，y2，…，ym]T。设有P个学习样本矢量，对应的期望输出为d（1），d(2)，…，d(p)，学习是通过误差校正权值，使各y(p)接近d(p)。为简化推导，把各计算节点的阈值并入权矢量。

　　该学习规则的推导是基于最小均方误差准则，当一个样本（设为第p个样本）输入网络，并产生输出时，均方误差应为各输出单元误差平方之和，即：

　　设sp为网络中的一个连接权值，则根据梯度下降法，批处理方式下的权值修正量应为：

　　由于BP网络采用的是基于梯度的最速下降法，有可能存在学习算法收敛速度慢和存在局部极小点的问题，可以采用Lenvenberg-Marquardt（L-M）法对网络进行改进，该算法实际上是梯度下降法和牛顿法的结合，其权重调整值如式（13）所示：

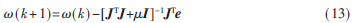
　　式中，J为网络误差对权值导数的雅克比矩阵；e为误差向量；I为单位矩阵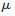；为标量，在计算过程中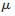，是自适应调整的，当其很大时，上式接近于梯度法，当其很小时，上式变成了高斯-牛顿法[14]。

　　根据Kolmogorov定理，任一连续函数或映射可由一个三层神经网络来实现，即一个三层的BP网络可以完成任意n维到m维的映射。因此本文采用三层BP神经网络来实现油特性参数的预测。

　　以导则中所给的实例为例，由于实例中所取的测量时间点只有6组，数据较少，在导则给出的油指数x和油时间常数o的推荐值基础上，在合理范围（±10%）内对两参数进行取值，得到100组数据，这100组数据中并未包含实例中的6组数据。根据公式o=a+o，其他参数采用实例中给出的值，计算出对应的顶层油温度，这样就有了100组包含各个所需参数的数据库。

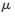　　网络的输入和输出是由实际问题决定的，本文将环境温度a、初始顶层油温升oi、负载系数K和顶层油温度o作为输入量，油指数x和油时间常数o作为输出量。由于前向BP神经网络是一个静态网络，在此为网络中引入记忆，即通过延时单元把网络输入量前一时刻的状态保留下来作为下一时刻的输入，每一时刻的初始油温升都是上一时刻的顶层油温升，从而使得静态网络变为动态网络。

　　隐含层的选择直接决定着神经网络训练程度的好坏。本文在训练中参考了多种经验公式[15]，采用试探法确定网络隐含层节点数，如式(14)。表3列举了BP网络所采用的几组隐含层节点数目。

　　式中，l为隐单元数，n为输入单元数，m为输出单元数，∈[1，10]区间的常数。

　　对每个隐层节点数都进行10次不同的训练，取平均训练误差最小时的节点数为最优隐含层节点数。最终当隐含层节点数为10时误差最小，于是选定隐含层节点数为10。

　　为了能够准确地进行预测，应该在训练之前对样本数据进行预处理，对于标准的sigmoid函数来说，其输入输出范围限定在[0，1]之间，则对训练样本进行归一化处理如下：

　　式中，y为样本经过归一化后神经网络的输入值，xi为实际的输入数据，xmax、xmin分别为实际输入数据的最大值和最小值。经过预处理后神经网络的输出值范围在[0.1，0.9]区间内，只需对式（15）进行一次反变换，即可转换为所需的热点温度值。

　　神经网络的学习过程需要数据进行训练，从而学会其中的内在规律，所以在检验网络的性能时，要用训练样本以外的数据。因此，把数据分为两组，一组用于训练神经网络，即为训练集；一组用于检验训练成果，称为测试集。本文中取80组数据作为训练集，20组数据作为测试集。在得到合适的网络之后，将得到的油热特性参数代入到式（1）中进行计算，结合文献[10]中的算法改进，将预测得到的热点温度与实例中给出的热点温度进行比较。

　　此外，为了使网络预测更精确，本文选用L-M算法改进传统的BP网络，设置训练目标为0.001，训练步长为50步，为了满足输出层范围在[0，1]之间，输出层选择S型对数函数logsig，为了保证隐含层传递的非线性特征，隐含层传递函数也采用logsig函数。

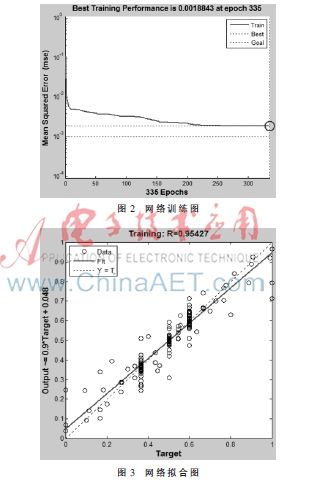
　　对神经网络进行训练。图2为Performance图，即网络训练过程图，由图2可知，最终训练误差只有0.001 88，训练结果良好。图3为Regression图，其反映的是网络的拟合能力，曲线越接近R=1，说明拟合能力越强，由图3可知，R=0.954 27，网络的拟合能力很好。

　　利用训练好的网络对实例中给出的6组数据进行预测，得到的结果如图4和表4。图4反映了随着负载和时间的变化，导则计算值、神经网络预测值和实际测量值的变化，由图可知，通过本文算法得到的温度值比导则算法更接近实际值。表4为每个负载级结束时，三种方式得到的热点温度值，同样可以发现神经网络预测值比导则计算方法更加准确。

5 结论

　　根据变压器发热机理，考虑环境因素和温度变化对油热特性参数带来的影响，以改进的导则热点温度计算方法为基础，结合采用L-M算法优化的神经网络算法，选取合适的函数和参数，训练网络并预测动态变化的油热特性参数，进而计算得到热点温度。将预测结果与IEC 60076推荐算法和实际测量值相比较，结果表明优化的神经网络算法对热点温度的计算值更接近实际测量值。

参考文献

　　[1] 谢毓城.电力变压器手册[M].北京：机械工业出版社，2003.

　　[2] 彭惠.变压器漏磁场及箱体涡流损耗计算[D].北京：清华大学，2004.

　　[3] 王晓莺.变压器故障与监测[M].北京：机械工业出版社，2004.

　　[4] 毛一之，王秀春，韩鹏.应用绕组测温装置测量变压器绕组温度的必要性和可行性分析[J].变压器，2004，4(9)：13-17.

　　[5] 钱政，孙焦德，袁克道.电力变压器绕组热点状态的在线监测技术[J].高电压技术，2003，29(9)：26-28.

　　[6] 陈淑谨，王世阁，刘富家.变压器绕组热点在线监测装置的研制与应用[J].变压器，2000，37(8)：41-45.

　　[7] IEEE.IEEE Std C57.91-1995 IEEE guide for loading mineral-oil-immersed transformers[S].Piscataway，NJ，USA：the Institute of Electrical and Electronics Engineers，1995.

　　[8] GB/T15164-2008.油浸式电力变压器负载导则[S].北京：国家技术监督局，2008.

　　[9] LESIEUTRE B C，HAGMAN W H，KIRTLEY J L.An improved transformer top oil temperature model for use in an on-line monitoring and diagnostic system[J].IEEE Transactions on Power Delivery，1997，12(1)：249-256.

　　[10] SUSA D，LEHTONEN M，NORDMAN H.Dynamic thermal  modelling of power transformers[J].IEEE Transactions on Power Delivery，2005，20(1)：197-204.

　　[11] SUSA D，NORDMAN H.A simple model for calculating transformer hot-spot temperature[J].IEEE Transactions on Power Delivery，2009，24(3)：1257-1265.

　　[12] 曾红，周孝信，吴青华.用智能学习方法建立电力变压器动态温度计算模型[C].中国供电国际会议，上海，2000：471-473.

　　[13] 陈伟根，赵涛，江淘莎，等.改进的变压器绕组热点温度估算方法[J].高压电器，2009，45（1）：53-56.

　　[14] 李孟励.基于BP神经网络的变压器绕组热点温度预测方法研究[D].重庆：重庆大学，2010.

　　[15] 陈慧琴.基于人工神经网络的遗传算法理论及应用[D].武汉：武汉理工大学，2003.