夏苏，朱磊，刘笑辰

　　(中国人民解放军理工大学 通信工程学院, 江苏 南京 210007）

　　摘要：为了更好地研究复杂网络抵制相继故障的鲁棒性，在经典的负载-容量模型基础上，提出了一种基于负载局域分配的相继故障模型。结合现实网络特点定义了衡量相继故障程度的指标——网络效率，提出节点对超出负载具有一定的容忍能力。将所提出的相继故障模型应用于经典复杂网络模型均观察到发生了相继故障现象，且通过仿真研究了相继故障传播的影响因素。实验结果表明，不同的节点失效方式、模型参数值以及网络的介数分布都会影响相继故障的传播。

　　关键词：复杂网络；相继故障；节奏效率；BA无标度网络

0引言

　　复杂网络［1］中的相继故障是指一个或者几个节点（或边）发生的故障会通过节点之间的相互关系引起其他节点发生故障，产生连锁效应并最终导致部分或整个网络的崩溃［2］。相继故障是复杂网络系统中一种常见的现象，一旦发生对系统的危害极大。现实生活中，发生相继故障的潜在可能性普遍存在于基础设施网络中，如电力网、供水网、交通网和通信网等［35］。2003年8月14日，由美国俄亥俄州克利夫兰市的3条超高压输电线路相继过载烧断引起的北美大停电事故，其影响区域包括美国东北部、中西部和加拿大东部，造成的损失高达数百亿美元，该事件的发生震惊了全世界。2007年，美国次贷危机除席卷了美国本土之外还影响了欧盟、日本等世界主要金融市场。类似的事件还有大规模的交通网阻塞、发生在因特网上的病毒传播等，这些都可以看作由相继故障导致的灾难性后果。

　　现实生活中的许多网络都可以看作为复杂网络，在以往的研究中，复杂网络的静态特性吸引了很多学者的注意［6］。然而，随着相继故障这一现象的出现，人们开始意识到复杂网络的动态特征也十分重要，因此越来越多的研究人员开始把目光聚焦到复杂网络的动态特征研究上。在此后的针对相继故障的研究中，陆续有人提出了复杂网络上的相继故障传播模型，并尝试提出减轻相继故障给复杂网络带来的不良影响的方法［7］。参考文献［8］考虑节点的动态特性提出了经典的ML模型，参考文献［9］综合考虑节点和边的动态特性提出了CLM模型。这两种经典模型都假设当一个节点失效时，其承载的负载会重新分配给网络中剩下的节点，这种全局分配的方式要求网络中所有节点实时了解全局信息。然而在现实生活中，复杂网络中的所有节点实时获取全局信息较为困难，并且这种方式的成本也较高。此外，在经典的ML模型中，节点的负载一旦超出它的容量，将被立即从网络中移除。但是现实网络中的一些节点，例如路由器，具备一定的拥塞承受能力，并且可以在一定范围内处于超负载工作状态。

　　本文提出了一种基于负载局域分配的相继故障模型，并给予每个节点一个初始的效率，当复杂网络中单个节点的负载超过它的容量，并且超出的比例在一定范围内时，假设这个节点不立即失效而是可以继续工作，同时，节点的效率将会大幅度降低。当节点负载超过节点可以容忍的阈值时，节点的效率降为0，其承担的负载将会分配给与其直接相连的邻居节点。

1基于负载局域分配的相继故障模型

　　在大多数的复杂网络中，节点都承担着一定的负载。对于一个给定的网络，信息或者能量通过最短路径在节点对之间进行交换，因此有理由认为节点的初始负载与经过它的最短路径条数有关，由此定义节点的初始负载等于其介数——网络中所有最短路径中经过该节点的路径数目占最短路径总数的比例，则节点i的初始负载用式（1）表示：

　　Li=Bi(1)

　　其中Bi为节点i的介数：

　　式(2)中，Sjk表示节点j到节点k的最短路径条数， Sjik表示节点j到节点k的最短路径中经过节点i的条数。这里所使用的介数定义中，将最短路径中处于两端位置的节点也考虑在内，这样就避免了有些节点的介数为0导致其在网络中不承担任何负载这一问题。本文提出的模型中，节点i的容量Ci表示节点保持最高效率正常工作时可以承担的最大负载。在现实生活中，节点的容量受成本的限制而不可能无限大。节点的容量反映了节点高效率处理负载的能力，因此很自然地假设节点的容量与节点的初始负载正相关，即：

　　Ci=(1+α)Li,i=1,2,...,N(3)

　　其中α是一个可调参数，并且α≥0，N是复杂网络中最初的节点总数。

　　考虑到本文关注的是单个节点从网络中被移除所带来的影响，因此此处假设网络中故障最开始只由一个节点的移除（节点失效）引起，并且节点失效后，该节点所承担的负载将会重新分配给网络中的其他节点。对于负载的重新分配，目前主流的方法有两类：一类是全局分配，即由网络中剩下的所有节点参与失效节点的负载的重新分配［10］；另一类是局域分配，即由该失效节点的邻居节点参与负载的重新分配［11］。但是在复杂网络中，相比于获取邻居节点的信息，获取全局信息要更加困难，并且保证所有节点实时获取网络中全局信息的成本也更高。基于以上考虑，本文采用局域分配的方法来重新分配失效节点的负载。这就意味着最开始时如果节点i从复杂网络中被移除，其承担的负载将会分配给与其直接相连的邻居节点。假设节点j是节点i的一个邻居节点，则节点j在负载重新分配后承担的负载用式（4）计算：

　　其中Ljd表示节点j的新负载，Li、Lj分别表示节点i和节点j在移除节点i之前各自承担的负载，此处由于节点i是网络中第一个失效的节点，因此也是它们的初始负载。ej是节点j的效率，将在下一节讨论。

　　2网络故障程度的评价指标

　　在以往的相继故障研究中，节点的状态往往只有正常或者失效一种，但是在现实生活中，复杂网络中的节点状态有时可以介于正常和失效两种状态之间。因此用节点效率来描述节点所处的状态，并用较高的效率来表示节点工作于一种更好的状态。

　　定义节点的初始效率为一个定值，节点i的初始效率用ei0表示，本文中令所有节点的初始效率都为1，即ei0=1，此时网络中所有节点都正常工作。当首个从网络中被移除的节点为节点i时，节点i的效率ei=0，且节点i的负载将会按照式（4）进行分配，其邻居节点接受节点i分配的负载后需按照式（5）重新计算各自的效率，即：

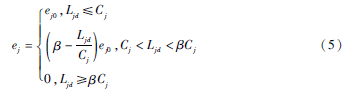
　　其中节点j为节点i直接相连的邻居节点。β为容忍参数，使得节点的负载在超出节点容量一定范围内时可以工作于一个较低的效率而不是立即失效，1<β≤2。容忍参数的存在使得当节点的负载超过其容量不是很多时不至于立即从网络中移除，这个机制也使得相继故障模型更加贴合实际，例如通信网络中的路由器，当其需要处理的流量超出路由器的容量时，路由器往往不会立即失效无法工作，而是使得丢失一部分数据包的概率变大，路由器的这种丢包行为就可以视为路由器工作于一种效率较低的状态。值得注意的是，虽然容忍参数β的值越大，意味着节点忍受超负载工作的能力越强，但是这也意味着在建设网络时要付出的成本更高，因此β的值并不能太大。

　　式（5）描述了第一个节点故障时（此时也为故障的第一个步长）的情形，将这个结论推广到第t个步长，将会得到故障第t次传播时各节点的效率，即：

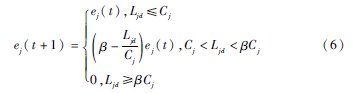
　　当节点的效率降为0时，该节点的负载将会分配给其邻居节点，此时该节点失效且其所有的邻居节点将会重新计算各自的效率。如果负载重新分配这一过程导致了新的节点发生故障，即发生了相继故障现象，新失效节点的负载将会继续分配给仍在工作的节点，因此又将引发新一轮的节点效率的计算。这个过程不断重复直至不再有新的节点故障，或者网络中所有的节点都出现故障。

　　当最终网络处于一种稳定状态时，用网络效率E(G)来衡量相继故障对复杂网络带来的损害程度。

　　E(G)=1N∑i∈Nei(7)

　　其中N是复杂网络的初始节点总数。网络效率E(G)反映了相继故障给复杂网络带来的不良影响，E(G)的值越小，表示整个网络的故障程度越高，对网络造成的伤害越大，当E(G)为0时，表示整个复杂网络中的所有节点都因故障失效而无法工作。同时，当最后网络稳定时，网络效率E(G)的值越大，可以在一定程度上反映网络在当时条件下有越好的抵御相继故障的能力。

3仿真结果与分析

　　3.1不同节点失效方式对相继故障传播的影响

　　为了研究在本文提出的模型下，故障在复杂网络上的传播情况，首先在BA无标度网络中进行实验。初始时节点总数N=1 000。首个节点失效采用两种方式——随机攻击和蓄意攻击。

　　当网络的其他参数一样，只有首个节点失效的方式不同时，通过仿真比较随机从网络中移除一个节点与有选择地移除网络中介数最大节点对网络效率的影响，仿真结果如图1所示。

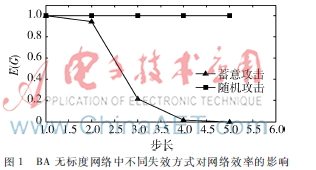
　　从图1可以看出，在BA无标度网络中，如果最先失效的节点是随机选取的普通节点，则由该节点引起的故障程度很小；而如果最先失效的节点是网络中介数最大的节点，则随着故障的不断传播，最终会引起相当多的节点失效。这也可以理解为BA无标度网络对随机攻击表现出相当强的免疫能力，但是在蓄意攻击面前却显得十分脆弱。

　　3.2模型参数对相继故障传播的影响

　　在研究网络中的可调参数α对相继故障传播的影响时，通过仿真研究了在β值一定时，最终的网络效率随α值的改变而变化的情况。仿真的网络选择BA无标度网络，首个节点失效的方式分别采用随机攻击和蓄意攻击的方法，仿真结果如图2所示。

　　从图2中可以看到，BA无标度网络在随机攻击时，网络效率一直很高，但是效率值呈现出震荡的走势；在首先移除介数最大节点时（蓄意攻击），在α大到一定程度时，网络效率随α的增大而增大。

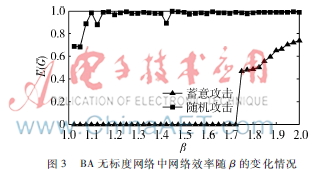
　　考虑到网络的容忍参数在相继故障模型中起着同样重要的作用，通过仿真研究了在α值一定时，最终的网络效率随着β值的改变而变化的情况。仿真条件与图2中相同，仿真结果如图3所示。通过对仿真曲线的对比分析可以发现，当随机选择最先失效的节点时，虽然网络效率随β有一定的波动，但整体上保持了一个较高的值，而当介数最大节点最先失效时，最终网络效率的值在β=1.7以后才随着β的增大而增大，并且即使β=2时，网络的效率也才在0.7左右。这也从侧面反映了介数最大节点对BA无标度网络中相继故障的传播有重要作用。

　　为了研究提出的相继故障模型在不同复杂网络中的表现，将模型应用到WS小世界网络，以便与BA无标度网络中的情形进行对比。仿真结果如图4、图5所示。可以看到，在α与β都较小时，WS小世界网络对移除介数最大的节点十分敏感，但是当这两个参数的值较大时，WS小世界　　

　　图5WS小世界网络中网络效率随β的变化情况网络对随机攻击和蓄意攻击均表现出了较强的抵御能力。且通过对比图2与图4以及图3与图5可以看到，为使网络保持较高的效率，WS小世界网络所需的α与β值比BA无标度网络要小得多，这意味着WS网络比BA无标度网络具有更好的抵御相继故障的能力，且通过合理增加α与β的值，可以使WS小世界网络对相继故障有较强的免疫力。

　　3.3改变节点介数分布对相继故障传播的影响

　　本文提出的相继故障模型定义的节点初始负载等于节点的介数，且节点的容量与节点初始负载正相关，因此节点的介数在模型中有着十分重要的作用，值得进一步研究。考虑在BA无标度网络中，在不改变节点之间连接关系的条件下，人为改变网络中节点的介数分布情况，使网络的介数分布更为均匀。仿真结果分别如图6、图7所示。

　　从图中可以看出，在BA无标度网络中，随机攻击时介数的改变对相继故障的传播影响不大。但是当介数最大的节点最先失效时，对于介数分布均匀的网络，相继故障对其造成的破坏程度要小。

4结论

　　本文通过建立相继故障模型，展示了一个很小的初始扰动可能导致网络中相当多的节点甚至整个网络崩溃。在本文提出的模型中，节点失效后采用了负载局域分配这一策略，考虑到节点对超出负载具备一定容忍能力，提出了相应的相继故障规模评价指标——网络效率。相关的仿真表明，节点的移除策略对相继故障的传播有着重要影响，即网络对网络中介数最大的节点失效更为敏感。同时，模型中参数α与β的大小也影响着网络相继故障的传播和最终的网络效率E(G)，并且合适的参数值在一定程度上可提高网络对相继故障的抵御能力。通过对仿真结果的分析可以发现，复杂网络的统计特征量如介数也可以影响到相继故障的传播。

　　本文的结论可以帮助理解相继故障的传播机理，并且对在建设网络之初参数的选择起到辅助决策的作用。虽然选择合适的参数并用于网络构建可以在一定程度上提高复杂网络的可靠性，但是对于已经存在的固有参数不那么合适的复杂网络，如何减小网络发生相继故障的概率，或者在故障已经出现时如何减小相继故障规模还有待深入的研究。

参考文献

　　［1］ 汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用［M］. 北京：清华大学出版社, 2006.

　　［2］ 丁琳, 张嗣瀛. 复杂网络上相继故障研究综述［J］. 计算机科学, 2012, 39(8):813.

　　［3］ Zhang Guidong, Li Zhong, Zhang Bo, et al. Understanding the cascading failures in Indian power grids with complex networks theory［J］. Physica A: Statistical Mechanics & its Applications, 2013, 392(15):32733280.

　　［4］ Shuang Qing, Zhang Mingyuan, Yuan Yongbo. Node vulnerability of water distribution networks under cascading failures［J］. Reliability Engineering & System Safety, 2014, 124(4):132141.

　　［5］ CHONG P Y, SHUAI B. Model of cascading failure in hazardous materials transportation network under series of terrorist attacks［J］. Systems EngineeringTheory & Practice, 2014, 34(4):10591065.

　　［6］ KASTHURIRATHNA D, PIRAVEENAN M, THEDCHANAMOORTHY G. On the influence of topological characteristics on robustness of complex networks［J］. Journal of Artificial Intelligence & Soft Computing Research, 2014, 63(2):89100.

　　［7］ TRAN H A Q, NAMATAME A. Mitigating cascading failure with adaptive networking［J］. New Mathematics and Natural Computation, 2015, 11(2): 151163 .

　　［8］ MOTTER A E, LAI Y C. Cascadebased attacks on complex networks［J］. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2002, 66(2):114129.

　　［9］ CRUCITTI P, LATORA V, MARCHIORI M. Model for cascading failures in complex networks［J］. Physical Review E, 2004, 69(4):266289.

　　［10］ 王建伟. 网络上的相继故障模型研究［D］. 大连:大连理工大学, 2010.

　　［11］ 王建伟, 荣莉莉, 王铎. 基于节点局域特征的复杂网络上相继故障模型［J］. 管理科学学报, 2010, 13(8): 4250.