郭亚伟,白治江

　　(上海海事大学 信息工程学院,上海 201306)

　　摘要：针对传统的SVM算法在非平衡数据分类中分类效果不理想的问题，提出一种基于分类超平面和SMOTE过采样方法(HB_SMOTE)。该方法首先对原始训练样本集使用WSVM算法找到分类超平面，然后按一定标准剔除负类中被错分的样本、靠近分类超平面的样本以及远离分类超平面的样本。在UCI数据集上的实验结果表明：与RU_SMOTE等重采样方法相比，HB_SMOTE方法对正类样本和负类样本都具有较高的分类准确率。

　　关键词：非平衡数据集；SMOTE；分类超平面；SVM；混合重采样

0引言

　　支持向量机(SVM)［1］因其能够有效地避免维数灾难，实现全局最优，具有严谨的理论基础和良好的泛化能力，现已成为机器学习领域的热点问题。传统的SVM方法需要其各类样本集的规模相同。然而在现实生活中，往往会遇到一些非平衡数据分类问题，如入侵检测、文本分类、医疗诊断等。使用这些数据对SVM方法进行训练建模时，分类决策面会向少数类偏移，导致少数类的分类准确率降低。国内外学者针对此类问题进行了深入的研究，提出了许多不同的处理方案。

　　目前，针对非平衡数据下SVM分类问题的研究主要集中在算法层面和数据重采样两个方面。算法层面主要是代价敏感性方法。这种方法虽然增加了少数(正)类的分类准确率，但却牺牲了多数(负)类的分类准确率，总的分类效果也受到了极大的影响［2］。数据重采样技术主要是过采样和欠采样。过采样主要包括随机过采样、SMOTE［2］算法、BorderlineSMOTE［3］技术等。这些过采样方法虽然可以确保原始分类信息的完整性，但是由于新合成的正类样本不能准确表达原始样本集的信息，从而导致过拟合，同时也会增加计算复杂度。欠采样主要包括随机欠采样、基于聚类欠采样的极端学习机［4］等。单一的欠采样技术虽然可以降低计算复杂度，但是在删除样本时通常会导致负类样本中部分信息缺失，影响分类准确性。

　　参考文献［5］表明相较于单一的采样方法，混合重采样方法往往能够得到更好的分类效果。参考文献［6］表明对于分类来说最重要的数据是位于边界的样本，噪声样本和距离分类边界较远的样本对数据信息的贡献不大。据此，本文提出了一种基于混合重采样和分类超平面的分类方法并在UCI数据集上进行建模训练，验证算法的有效性。

1基本的分类方法

　　1.1SMOTE算法

　　SMOTE算法［2］是由CHAWLA N V等人提出的一种过采样方法。该算法步骤如下。

　　（1)对正类中的每一个样本x，计算它到该类中其他每个样本的欧氏距离，获取其k个最近邻样本，并记录近邻下标。

　　（2)按照两类数据集不均衡的比率设置正类的采样倍率N,对所有正类样本x，从k个最近邻中随机选取xi(i=1，…，N)。

　　（3)对每一个近邻xi，分别与原始样本x按照xnew=x+rand(0,1)×(xi－x)合成新样本。

　　（4)把合成的新样本与原始训练样本集并为新的训练集，并在该样本集上学习。

　　1.2SVM与WSVM

　　SVM是在统计学习理论中结构风险最小化原则基础上提出的机器学习方法［1］。其原理是寻找一个最优分类超平面，使得该超平面在保证分类精度的同时，能够使超平面两侧的空白区域最大化。此外，它还能通过核函数将低维空间中的线性不可分问题转化为高维空间中的线性可分问题。设训练样本集为(xi,yi),i=1,2,…,l,x∈Rn,y∈{±1}，超平面记作(w·φ(x))+b=0，其中φ(x)为x从输入空间Rn到特征空间H的变换。将构造最优超平面问题转化为求解二次凸规划问题，即：

　　为解决由于样本集失衡导致的分类决策面偏移问题，引入了基于代价敏感的WSVM，主要思想是对错分的正类和负类样本分别赋予不同的惩罚系数C+和C-，约束表达式变为：

2混合重采样方法

　　2.1RU_SMOTE算法

　　许多学者综合考虑了过采样与欠采样的弊端和优点，提出两类采样方法同时使用的混合重采样方法［5］。RU_SMOTE算法［7］是一种使用随机欠采样与SMOTE相结合的混合重采样方法。算法思想为：先确定合成样本的比例γ，利用SMOTE算法增加相应比例的正类样本；然后使用随机欠采样删除负类样本，使数据达到平衡；通过改变γ调整合成样本的数量和数据规模；最后使用SVM分类。该算法既能去除负类样本降低数据规模，又能增添新的样本信息，缓解由于样本集失衡而带来的分类决策面的偏移。

　　2.2HB_SMOTE(Hyperplane Based SMOTE)算法

　　上述混合重采样方法虽然取得了比单一采样方法更好的分类效果，但并没有克服随机欠采样的盲目性。对于分类来说位于边界的样本为重要样本［6］，噪声样本和距离分类边界较远的样本则是次要样本，剔除这些样本不会引起太多的信息损失。基于这种思想，本文提出了一种改进的混合重采样算法：首先采用WSVM算法寻找分类边界，亦即分类超平面；然后按一定标准将被错分的和靠近分类超平面以及远离超平面的负类样本删除，再对正类利用SMOTE方法进行过采样使正负类数据达到平衡并且引入新的样本信息；最后使用SVM建模训练。

　　算法的具体实现步骤如下。

　　（1）使用WSVM算法对原始数据集进行训练，寻找分类超平面，即:f(x)=∑li=1α*yiK(Xi,X)+b*=0。

　　（2）确定SMOTE合成新样本的比率γ。对正类样本进行相应比率的合成过采样，组成新的正类样本集。

　　（3）对步骤（1）训练集中的每一个负类样本xi，计算xi到分类边界f(x)的距离di，并对di进行排序。

　　（4）对于排好序的di，选取n个最大的dj(j=1,2，…，n)和m个最小的dj(j=1,2，…，m)，分别从原训练集中删除与dj对应的这些n+m个点。将剩下的负类样本与步骤（2）中新正类样本一起作为新的训练集。

　　（5）对新的训练集使用SVM算法进行分类。

　　（6）可以选取不同γ、n和m重复步骤（4）以获取合适的新负类样本集。其中n和m决定于γ的变化。

3实验分析

　　3.1评价标准

　　许多传统的分类学习算法主要采用准确率(正确分类的样本数目占所有样本总数目的比率)作为分类学习的评价指标，它所对应的混淆矩阵［8］见表1。真实负类FPTN对于非平衡数据集而言，用准确率来评价分类器的性能是不合理的。因为很多情况下虽然总的分类精度很高，但实际上正类的分类精度却可能很低。如果正类样本数占总样本数的1%，即使正类样本全部分错，分类精度还是会达到99%。但这却是无意义的。因此需要采用新的评价方法。定义如下指标：

　　Acc+=TP/(TP+FN)

　　Acc－=TN/(FP+TN)

　　Precision=TP/(FP+TP)

　　Recall=TP/(TP+FN)

　　本文中，使用G_mean和F_measure作为评价准则:

　　G_mean=Acc+·Acc－

　　F_measure=2×Recall×PrecisionRecall+Precision

　　G_mean性能指标同时兼顾了正负类样本的分类性能，只有二者的值都大时，G_mean才会大，因此G_mean主要是代表了非平衡数据集的总体的分类性能。性能指标F_measure则综合考虑正类样本的查全率和查准率，只有二者的值都大时，F_measure才会大，所以它主要是度量分类器对正类的分类效果。

　　3.2实验

　　本文所采用的实验数据都来自于UCI机器学习数据库，分别为Glass数据集、Vowel数据集和Segment数据集。由于这3个数据集都是多类数据集，为简化起见，先将数据集都变为二类分类问题。对Glass数据集选取类标为“7”的数据作为正类，将其余的类合并作为负类。而对Vowel和Segment数据集分别选取类标为“hed”和“brickface”的数据作为正类。这3个数据集的详细描述详见表2。

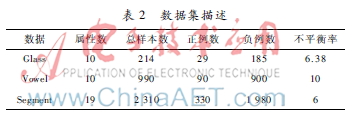
　　实验设计如下：使用MATLAB作为仿真环境并使用LIBSVM工具箱作为实现工具。本文采用10折交叉验证的方法对数据集进行验证，在实验中将本文的HB_SMOTE与SMOTE、随机欠采样、RU_SMOTE方法作对比，通过改变SMOTE新样本的比率得到不同比率下的分类结果，如表3~表6所示。

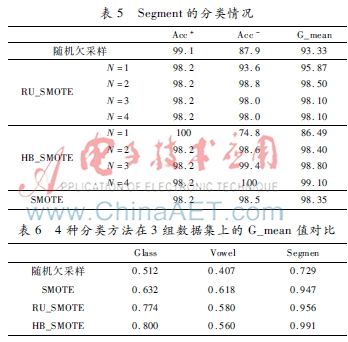
　　由表3~表5可以看出，SMOTE算法性能优于随机欠采样，主要因为随机欠采样算法随机删除样本的同时也将有用信息删除。而RU_SMOTE算法要优于SMOTE算法和随机欠采样算法，主要因为作为混合采样其综合了SMOTE算法和随机欠采样的优点。HB_SMOTE算法的G_mean和Acc－比其他3种算法高，表明其总体效果要优于其他3种算法，这是因为该算法剔除了负类样本集中的噪声样本和无用样本，从而增加了有效样本的比率。结合表3~表5可以看出，SMOTE合成新样本的比率不同，优化结果也不尽相同，通过改变SMOTE合成新样本的比率可以寻求更优的结果。由表6可以看出HB_SMOTE的值要优于其他3种方法，这表明该分类器在一定程度上能够提升正类的分类效果。

4结论

　　SVM在解决小样本、非线性分类问题上具有显明的优势，更重要的是其具有良好的泛化能力。但是在现实生活中广泛存在着非平衡数据分类的问题，传统的SVM算法对于少数类样本的识别准确率较低。本文基于SMOTE过采样技术提出了一种改进的混合重采样方法(HB_SMOTE)：首先通过WSVM找到分类超平面，据此删除那些负类样本集中越界和靠近超平面的样本以及那些远离超平面的样本，从而减少负类样本集中的噪声点和无效点。而通过SMOTE算法所合成的正类样本点则能够增加少数类样本集的信息量和密度。在UCI数据集上对比4种算法的实验结果表明，HB_SMOTE算法性能明显优于其他3种算法，表明该分类器在相对较少的增加运算规模的基础上能够提升少数类的分类精度。

参考文献

　　［1］ VAPNIK V N.The nature of statistical learning theory［M］.New