朱志成，黄波，刘南杰

　　(南京邮电大学 通信与信息工程学院， 江苏 南京 210003)

      摘要：针对非连续正交频分复用调制信号高峰均比特点，提出了一种新的降峰均比方法。首先，将符号序列进行离散傅里叶变换；接着，将变换之后的数据按照当前的频谱空洞分布以及后续旁瓣抑制处理，划分成一个或多个最小子载波数受限的数据载波块，并在数据载波块之间插入合适的零数据块予以扩展；最后，将扩展后的数据通过快速傅里叶逆变换实现调制。以闭式表达式的形式给出了原始符号和经过扩展调制之后的信号之间的关系，从理论推导和仿真分析验证了该技术的有效性和可行性。

　　关键词：非连续正交频分复用；峰值平均功率比；数据载波块；离散傅里叶变换扩展

0引言

　　与连续正交频分复用系统(Orthogonal Frequency Division Multiplexing，OFDM)相似，非连续正交频分复用(NonContinuous Orthogonal Frequency Division Multiplexing, NCOFDM)系统中同样存在高峰均比(PeaktoAverage Power Ratio, PAPR)问题［1］。基于信号畸变类降PAPR技术［2］会引起带内频谱扩展；基于编码类降PAPR技术［3］存在编码效率低下问题，尤其是子载波数越大效率越低。

　　在LTE上行链路中，为了降低移动台处理复杂度，引入了单载波频分复用技术(Singlecarrier FrequencyDivision Multiple Access, SCFDMA) ［4］。它首先将要发送的符号做离散傅里叶变换(Discrete Fourier Transform，DFT)，然后通过快速傅里叶迸变换(Inverse Fast Fourier Transform，IFFT)完成调制。与SCFDMA系统相类似的DFT扩展降PAPR技术［5］通过将待发送的M个符号做M阶的DFT后，按照一定的策略映射到N(N≥M)个子载波中，再经过N阶IFFT完成调制。

　　受SCFDMA及DFT扩展降PAPR技术的启发，同时考虑到NCOFDM系统旁瓣抑制技术［6］中广泛采用的子载波加权结合预留保护带方法［67］，本文提出一种基于数据载波块中最小子载波数受限的DFT扩展（Discrete Fourier TransformData Carrier Block, DCBDFT）降PAPR技术。该技术能够在降低NCOFDM系统PAPR的同时，兼顾后续旁瓣抑制处理。

1DFT-DCB降PAPR技术的原理

　　1.1DFT-DCB的实现方案

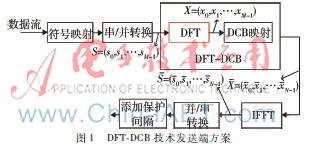
　　DFTDCB技术方案如图1所示。在发射端，待发射数据流经过符号映射并通过串并转换后得到符号序列S=(s0,s1,…,sM－1)，S经过DFT变换得到X=(x0,x1,…,xM－1)，X再按照一定的映射策略，实现DCB映射，得到信n=1N∑K－1k=0 ∑lDCB,k－1ii=0 ∑M－1idx=0sidxe－j2π∑knum=0lDCB,num－1+iiMidx×ej2πnN∑knum=0(lZero,num+lDCB,num－1)+ii(6)号=(0,1,…,N－1)，其中N≥M。再通过一个N阶的IFFT完成调制。在接收端存在一个相对应的逆处理过程，不再讲述。

　　1.2DFT-DCB降PAPR技术的理论分析

　　如图1所示，DCB映射后，信号经过IFFT，得到时间域信号=(0,1,…,N－1)，这里：

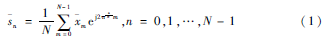
　　从式（1）可以看出，时间域信号的特性由DCB映射之后的m的分布决定，PAPR特性也不例外。m的分布由DCB映射策略确定，以DCB为单位，DCB映射过程如图2所示。

　　设第k个数据载波块DCB［k］的长度为lDCB,k，其中0≤k≤K－1，并且对任意k，要求lDCB,kLmin，这里的Lmin即为了兼顾旁瓣抑制而对数据载波块子载波数的最小要求。数据载波块DCB［k］之间和数据载波块序列的首尾插入长度为lZero,k的零元素块ZERO［k］={0,…,0}，一方面是考虑授权用户使用频段，另一方面为了减少对授权用户的干扰而预留的保护带，其中0≤lZero,k，0≤k≤K。参照式(1)，扩展之后的数据经过IDFT，得到调制之后的信号为：

　　其中，DCB［k］［ii］表示第k个数据载波块DCB中的第ii个元素，ii≥0，并且：

　　原始符号S经过DFT得到待发射信号向量X中的元素：

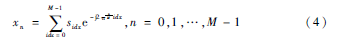
　　X被分隔成K个DCB块，可得DCB［k］［ii］和X元素之间的对应关系：

　　将式(3)和式(5)代入式(2)可得到：

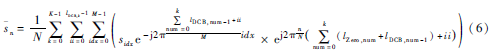
　　式(6)表达了原始的符号序列S经过DC-DFT扩展，再经过IFFT之后的发射信号。显然，在S一定的情况下，的PAPR特性由lDCB,k、lZero,k决定，或者说由DCB的映射策略决定。从式(6)可以看出，很难从数学上对一般情况下的DCB-DFT性能进行分析，需要通过仿真实验进行统计分析。

2仿真及结果分析

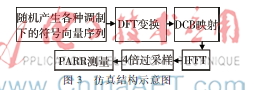
　　为了验证DFTDCB技术的有效性和可行性，建立仿真结构如图3所示。

　　考虑实际应用情况，仿真中调制方式选择常用的QPSK和16QAM；总的数据子载波数M分别取32和256，以分别对应窄带应用场景和宽带应用场景；仿真中采用5 000组随机产生的符号序列，以统计到10－3概率下的PAPR特性，IFFT和FFT计算中子载波数取N=1 024。　

　　现实中频谱空洞分布具有随机性，仿真中随机选择每个DCB中子载波的大小（不小于Lmin=8），并且随机插入一定数目的零填充块，同时要注意保持扩展之后的数据长度N=1 024。因为无法一一列举，仿真中统计了104次的随机序列输入仿真结果，如图4和图5所示。　

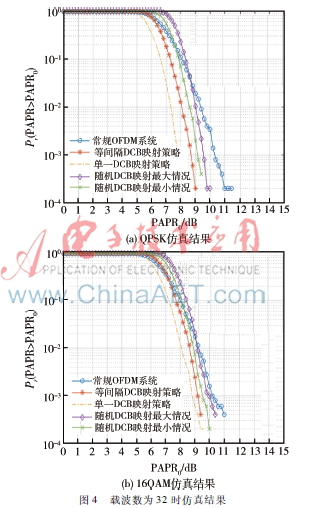
　　从图4和图5可以看出，QPSK和16QAM两种调制方式下，DFT-DCB技术对传统的OFDM传输系统的PAPR性能都有较好的改善效果。在10－3概率处，对于QPSK调制方式，总数据载波数为32和256时，能够获得最差大约1 dB的PAPR改善；而对于16QAM调制方式，总数据载波数为32时，能够获得的最差PAPR改善性能非常有限，总数据载波数为256时，能够获得最差大约1 dB的改善性能。这也说明DF-DCB性能与调制方式以及具体的映射策略密切相关。

3结论

　　理论分析和仿真结果均表明，本文提出的DFTDCB技术能够有效降低NC-OFDM系统的PAPR，降低的性能与调制方式、总数据载波数以及映射策略密切相关。同时，DFT-DCB通过限制DCB中子载波最小数目，为NC-OFDM系统后续的旁瓣抑制处理提供了便利。

参考文献

　　［1］ RAHMATALLAH Y， MOHAN S. Peaktoaverage power ratio reduction in OFDM systems: a survey and taxonomy［J］. IEEE Communications Surveys & Tutorials, 2013, 15(4):15671592.

　　［2］ Wang Y C,Luo Z Q. Optimized iterative clipping and filtering for PAPR reduction of OFDM signals［J］. IEEE Transactions on Communications, 2011, 59(1):3337.

　　［3］ Qu Daiming, Li Li, Jiang Tao. Invertible subset LDPC code for PAPR reduction in OFDM systems with low complexity［J］. IEEE Transactions on Wireless Communications, 2014, 13(4):22042213.

　　［4］ MYUNG H G, LIM J, GOODMAN D J. Single carrier FDMA for uplink wireless transmission［J］. IEEE Vehicular Technology Magazine, 2006, 1(3):3038.［5］ YONG S C,JAEKWON K, WON Y Y, et al. MIMOOFDM wireless communications with MATLAB［M］. Singapore: WileyIEEE Press, 2010.

　　［6］ KUMAR R,TYAGI A. Sidelobe suppression using differential coding in OFDM cognitive radios［C］. IEEE International Conference on Signal Processing, Computing and Control (ISPCC), 2013:16.

　　［7］ COSOVIC I, BRANDES S, SCHNELL M. Subcarrier weighting: a method for sidelobe suppression in OFDM systems［J］. IEEE Communications Letters, 2006, 10(6):444446.