徐振武，徐志京

　　(上海海事大学 信息工程学院，上海 201306)

　　摘要：经典的Harris算法在提取图像的角点上具有计算简单、适应性强等优势，但该方法由于人为设定单一阈值，容易出现伪角点、漏检点及运行速度不理想等现象。针对这一情况，文章在传统Harris算法基础上提出一种新的检测方法，采用多阈值的圆形非极大值抑制法提取角点, 以此降低算法检测时间并增强图像旋转不变性，再借鉴SUSAN思想消去大部分伪角点。通过实验对比，该算法具有更好的角点检测性，为后期的图像配准奠定了良好的基础。

　　关键词： Harris角点检测；圆形区域；多阈值；SUSAN算法

0引言

　　随着近代计算机的迅速发展，人们为了获取更高像素更宽视角的图像以作科学研究，图像拼接逐渐成为了计算机各领域的研究热点［12］。

　　图像蕴含有丰富的信息特征，其中角点特征是图像拼接领域的主要技术指标，业界对角点没有统一定义，一般被认为是图像像素点亮度发生了剧烈改变或边缘曲线曲率极大值的点［3］， 它能以极少的数据量来表现图像的整体信息， 这有利于图像处理的速度与精度。角点检测方法在图像拼接中的配准、融合、 定位等方面起着重要作用， 其提取的好坏决定图像拼接的质量结果。适量恰当的正确角点在图像拼接过程中可增强图像的抗噪性和图像形变的适应能力，有利于图像的后续匹配,使得实时处理成为可能。

　　目前角点的检测方法大致分两种：基于图像边缘特征的角点检测, 该算法依赖于图像边缘特征［4］，提取边缘信息而求得角点，但算法定位精度差，对噪声敏感；基于图像灰度的角点检测，该方法依赖于像素点的曲率与梯度值信息。其中Harris算法［5］是一种被大众所熟知的算法, 可较好地提取角点。该算法虽然是一种优秀的检测方法, 但研究发现存在不足:

　　（1）人为单一阈值的设定会对角点提取产生不确定的影响；

　　（2）算法中所用的高斯平滑函数对图像的误检及漏检产生难以把控；

　　（3）Harris算子的运行速度不够理想。

　　而对Harris的改进一直是图像研究的热点，参考文献［6］提出采用自适应阈值的方法能达到更快更精确提取角点的效果，但在图像的抗噪性和适应图像形变能力上略显不足；而参考文献［7］提出的改进方法能满足要求，但在运算速度上又略显欠缺。

　　针对上述不足，本文提出基于Harris的改进方法，采用多阈值的圆形区域非极大值抑制，再结合SUSAN思想达到检测效果。

1Harris角点检测算法简介

　　角点检测的鼻祖是Moravec算法，之后Harris在Moravec算子思想上提出Harris算法。

　　Harris算法的思想是定义一组矩形区域窗口中图像灰度误差的总和为任意方向上的自相关值［8］。图1表示图像边缘在不同区域的变化情况。图1(a)、(b)窗口在边缘上没变化，而(c)的窗口在各个方向上具有明显的变化，根据此现象，可将(c)作为角点。

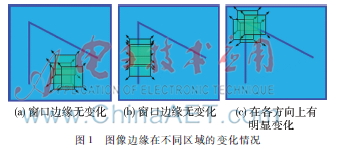
　　窗口平移［u,v］的量产生的图像灰度变化E(u,v):

　　E(u,v)=∑x,yw(x,y)［I（x+u,y+v）-I(x,y)］2(1)

　　由I（x+u，y+v）=I(x,y)+Ixu+Iyv+O(u2+v2)

　　得：　

　　由于矩阵M=AC

　　CB特征值不易计算，通常计算式(5)，R为角点响应值(CRF)，大小为：

　　R=detM－k(traceM)2(5)

　　其中，detM=λ1λ2=AC－B2,traceM=λ1λ2=A+C,detM是矩阵M的行列式;traceM是矩阵M的迹;k是经验常数，取0.04~0.06。若R>CRFmax，则此像素点可提取为角点。

　　为了避免在求CRF时设定k，这里参考文献［7］：

　　R=［I2x*I2y-(IxIy)2］/(I2x+I2y+ε)(6)

　　ε表示任意小的正数。

2改进的Harris角点检测算法

　　2.1算法思想

　　本文采用多阈值方法。首先设定初始阈值并采用圆形区域非极大值抑制来提取大部分的候选角点，之后对图像作等比分块处理。利用块的自适应阈值求块的补充角点。以此达到避免单一阈值下角点缺失或较多伪角点现象。

　　传统Harris算法常用3×3（大小可调）为模板区域对图像非极大值抑制：模板中心点与其余8点逐一比较大小，若中心点响应值大于其他任一模板内响应值，则该中心点被认为是角点。同理圆形窗口下以圆心作为中心点，若比较后中心点响应值最大，则作为候选角点提取，圆心位置顺序递增，相反则舍弃该点，进行下一轮非极大值抑制。

　　运用矩形模板区域非极大值抑制时，如果图像发生旋转变化，窗口也发生变化，因此增加了误检与漏检的风险。而根据圆的旋转不变性，采用圆形窗口能够提高图像旋转不变性。

　　2.2算法实现步骤

　　（1）初始角点RA提取

　　在初始阈值下，利用圆形区域进行非极大值抑制方法求得候选角点集合A并计算A中每个像素点的CRF值R，取最大Rmax0，令基础阈值：

　　T0=c0×Rmax0(7)

　　c0为常数。当c0取0.02~0.04 时可满足要求。

　　令R>T0且R为模板区域内极大值的点A，记为初始角点RA。

　　（2)块角点RB提取

　　将一个V×W图像切割为M×N块数量,块的尺寸为(V/M)×(W/N)。在块中求除了RA之外的Rmax值。将第［p,q］块的最大R记为Rmax B(p,q)，设置块阈值为:

　　TB(p,q)=cB×Rmax B(p,q)(8)

　　cB为常数，取值0.1~0.3时检测出的块角点RB能够很好地弥补初始角点的欠缺。

　　(3)SUSAN思想消除误检

　　SUSAN算法能消去误检点，并具有较好的抗噪性，其步骤：初置阈值s并定义一圆形模板，用此模板逐一比照图像每一区域。 若模板中心点（核）灰度值与模板内某像素点灰度差小于s，即该点与中心点(核)具有相似灰度值。所有类似的点组成的区域叫做USAN，SUSAN算法示意图如图2所示。　　

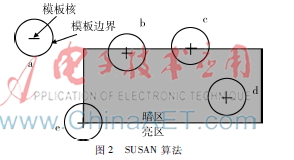
　　算法上, 用圆形模板扫描整幅图像, 当模板在灰色区域如图2中的d, USAN面积最大；当模板接近灰色区域边缘图b时，USAN面积慢慢减小；当核在灰色区域边缘时如图c， USAN面积很小；在核处于角上时如图e，USAN面积最小。

　　由此利用圆形模板扫描RA、RB可删除误检点。设像素点(m,n)为RB的角点,若以(m,n)为核的USAN面积大于1/2模板面积即认为该点为误检点。如此便可略去大部分误检点。

3实验结果与分析

　　对于改进Harris角点检测算法一直是图像拼接等领域研究的热点，针对Harris算子的不足，各方法的改进都侧有不同，本文结合传统Harris、参考文献［7］的改进算法做一个简单比较。

　　实验中，先采用一张角点较明显的图，对传统Harris、参考文献［7］及本文算法进行对比。为了客观比较，与参考文献［7］相同，本文传统算法阈值大小也采用1 200，比较结果如图3所示。　

　　图3(a)传统Harris算法中，提取出较多角点数量，且在这张角点分明的图像里，有着稍微的角点聚簇现象，而误检点数较其他两图亦是最多，且处理时间也比较长；而参考文献［7］与本文算法所得到角点分布图较为相近，角点数较传统算法有所减少，分布也较均匀。但对比两图，统计图中3种角点数量，如表1所示，不难看出本文算法更出色，其正确角点及漏检角点虽然相似，但误检数量更少，有利于图像拼接后续的配准工作。

　　本文所用圆形区域非极大值抑制，不但在运算时间上表2角点数量及算法运算时间对比算法图像1图像2图像3图像4图像5角点时间/s角点时间/s角点时间/s角点时间/s角点时间/s传统Harris算法1 551152.841 20092.1173818.723784.601801.12参考文献［7］算法1 332140.251 09787.5160515.32773.821700.98本文算法1 20888.0798774.4155610.512352.781620.78有优化，而且对图像旋转不变性也有不错的改善。图4是对图像作45°旋转后算法对比：

　　图4对图像作45°旋转后算法对比图4(a)对比图3（a)，经45°旋转后，传统Harris算法能提取出大部分的角点，但存在较严重的漏检现象。采用本文算法，对比图3(c)与图4(c)的图像旋转角点检测状况可知，旋转前后，均能很好地检测出角点，漏检与误检现象虽然存在，但比传统算法好。比较参考文献［7］方法，本文算法在采用圆形非极大值抑制后，具有更多的正确角点和更少的误检点。

　　Harris算子本身具有不错的抗噪性，但本文在采用SUSAN思想后能增强算法的抗噪性。图5是在0.1的高斯噪声下效果对比。

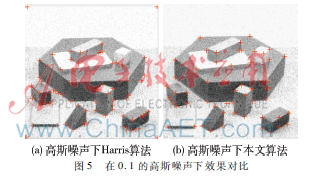
　　从图5可以看出，本文算法在高斯噪声环境下有不错的表现，特别是伪角点检测上。经过大量图像角点处理实验证明，本文算法在消除误检点效果上好于原算法，因此认为具有更强的抗噪性。

　　在图像处理的时间上，对比本文算法较传统算法也略有优势。为客观比较，本文采用上海海事大学信息工程学院为背景的图像，由Android手机拍摄，原图尺寸为：5 248×3 936，利用图像编辑软件进行等比例缩放，其尺寸分别为：3 726×2 794、2 624×1 698、1 312×984、656×492、328×246。

　　随着图像分辨率的降低，角点数也在减少，这是可预见的，因为高分辨率图像势必具有更丰富的细节信息，所能提取的角点数目也更多。由表2可知，相较于传统Harris和参考文献［7］算法，本文介绍的算法能在涵盖图像的特征情况下提取出相对少的角点，且运行速度也可圈可点，因此认为在算法性能上要好于另外2种。图6是表2的图像4，尺寸大小为656×492。

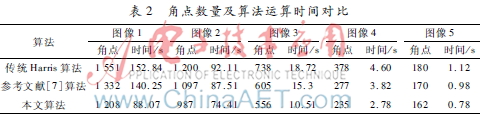
　　综上图示及表数据，本文算法在漏检、误检都有不错表现，利用该算法，能够很好地检测出正确角点，同时能改善传统算法在角点的聚簇现象，匀化角点分布，有利于后面的图像配准处理。

4结束语

　　在基于灰度的角点检测算法中，被大众所知的经典Harris算法具有不错的效果，能满足日常应用，并且对该方法的改进一直是一个热点话题。本文基于传统Harris算法在图像拼接领域应用的不足，提出改进思想，采用多阈值的圆形非极大值抑制法提取角点并利用SUSAN思想去除误检点，经实验证明，在运算时间及消除多余的误检点以及减少漏检现象上有明显的改善，具备比较好的角点检测性能，此方面的性能提升，可为后期获得更好图像拼接效果提供一个算法参考。

参考文献

　　［1］ TUYTELAARS T，MIKOLAJCZYK K． Local invariant feature detectors: a survey［J］.Foundations and Trendsin Computer Graphicsand Vision，2008，3(3): 177280．

　　［2］ 仇国庆，冯汉青，蒋天跃，等．一种改进的Harris角点图像拼接算法［J］．计算机科学，2012,39(11):264266

　　［3］ SMITH A M, BRADY J M. Susan: A new approach to low level image processing［J］ . International Journal of Computer Vision, 1997, 23(1): 4578.

　　［4］ HARRIS C, SATEPHENS M J. A combined corner and edge detector［J］. Image Vision Computting, 1988, 6(1): 121128.

　　［5］ 涂春平，柴亚辉，李广丽，等．一种基于Harris角点特征精确匹配的图像拼接方法［J］．实验室研究与探索,2011,30(10):4043.

　　［6］ 沈士喆，张小龙， 衡伟．一种自适应阈值的预筛选Harris角点检测方法［J］．数据采集与处理，2011，26（2）:207213.

　　［7］ 毛雁明． 一种改进的基于Harris的角点检测方法［D］．昆明： 云南师范大学，2009.

　　［8］ 龙伶敏． 基于Adaboost的人脸检测方法及眼睛定位算法研究［D］． 成都： 电子科技大学，2008.