党超，刘锋，曾连荪

　　（上海海事大学 信息工程学院，上海 201306）

　　摘要：应用信号对齐方法研究了多输入多输出双向中继3×2 X信道的自由度问题，并分析了其天线配置条件。然而，对于更一般的多用户X信道，随着用户数的增加，应用这一方案所需要的天线数也会迅速增加，在实际应用中难以实现。为缓解这一问题，该文进一步提出了基于时间扩展的解决方案。

　　关键词：自由度；信号对齐；时间扩展

0引言

　　*基金项目：国家自然科学基金（61271283）；上海教委科研创新项目（14YZ113）自由度表征了通信信道的传输能力。最基本的2×2 X 信道的自由度上界被证明是4A/3［1］，对于一般的M×N X 信道，自由度上界是AMN/(M+N－1) ［2］，这里A表示每个终端的天线数。双向通信模型很早被香农所提出［3］，并在无线中继网络中得到应用。在三用户MIMO Y 信道模型中应用信号对齐的方案，自由度可以在N≥3M/2时达到3M，这里N和M分别代表中继和终端的天线数［4］。本文将利用信号对齐结合网络编码的方案来分析应用双向中继3×2 X 信道的自由度问题，并进一步研究了一般情况下的实现方案。其中关于多值信号检测［5］、迫零矢量的设计已有很多论文涉及［6］，网络编码的方法也早已被提出［7］，此处不做深入介绍，而只应用其结论。

1信道模型

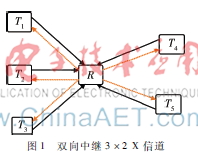
　　如图1所示，在多输入多输出（Multiple Input Multiple Output, MIMO）双向中继的3×2 X信道中，左侧三个终端希望分别传送一个消息给右侧的两个终端，同样右侧的两个终端也要分别传送一个消息给左侧的三个终端图1双向中继 3×2 X 信道，那么需要传送的消息总数是12个。借助双向中继，本文利用MIMO技术在同一时频资源上传输全部12个消息。假设左侧终端的天线数为Ai，右侧终端的天线数为Aj，中继的天线数为AR。

　　模型说明：任意两个终端无法直接通信，只能通过中继实现信息交流；所有的信道是准静态平坦的；信道元素取自具有零均值和单位方差的独立同分布的复高斯分布；所有的终端和中继都工作在全双工模式下。

2信号对齐方案

　　整个方案的实现分为两个过程：多址接入（Multiple Access, MAC）阶段和广播（Broadcast, BC）阶段。首先，在MAC阶段各终端把信号发送给中继，在中继处应用信号对齐和网络编码的方法得到包含所有消息的网络编码消息，然后中继在BC阶段把这些编码后的消息发送给各个终端，最后各终端利用自己发出的消息来得到期望消息。为了更方便地进行分析，这里首先把各终端和中继的天线数设定为Ai=3，Aj=4，AR=6，下面就这两个阶段作具体分析。

　　2.1MAC阶段

　　在MAC阶段，左侧的三个终端Ti(i=1,2,3)分别沿波束成形矢量vj,i发送消息xj,i给右侧的终端Tj(j=4,5)，同样地，右侧的终端也要沿波束成形矢量vi,j传输消息xi,j给左侧终端。则中继接收到：

　　yr=∑3i=1Hr,ixr,i+∑5j=4Hr,jxr,j+nr（1）

　　其中，Hr,i和Hr，j表示信道矩阵，nr表示具有零均值和单位方差的加性高斯白噪声，同时有：

　　xr,i=∑5j=4vj,ixj,i(i=1,2,3)（2）

　　xr,j=∑3i=1vi,jxi,j(j=4,5)（3）

　　满足功率约束条件E{tr［xr,ixHr,i］}≤Pi，E{tr［xr,jxHr,j］}≤Pj。

　　实现信号对齐的目的是把对发的消息对齐，形成一个包含两个对发消息的叠加消息，从而降低中继的维度要求，比如xr(1,4)=x1,4+x4,1。那么就要有：

　　span(Hr,1v4,1)=span(Hr,4v1,4)=span(ur(1,4))（4）

　　其中，span(A)表示由矩阵A的列向量张成的空间，而span(A)=span(B)代表了A和B所张成的子空间是相等的。要得到v1,4和v4,1，需要满足下式：

　　这里ur(1,4)就是取自两个信道矩阵的交叉空间的向量。而要保证上式中右侧的列向量存在，就要保证左侧的矩阵存在零空间，又因为该矩阵是12×13的，那么它至少具有一维的零空间，即保证了ur(1,4)，v1,4和v4,1的存在。那么式(1)变为：

　　yr=urxr+nr（6）

　　其中,ur=［ur(1,4)ur(1,5)ur(2,4)ur(2,5)ur(3,4)ur(3,5)］，xr=［xr(1,4)xr(1,5)xr(2,4)xr(2,5)xr(3,4)xr(3,5)］T。正如前面xr(1,4)=x1,4+x4,1，xr(1,5)=x1,5+x5,1，其他也是这样，那么共有6个叠加的消息，而中继有6条天线，所以有足够的空间解得这6个叠加的消息。然后应用网络编码的方法，将解得的叠加消息重新编码为新的发送消息r=［r(1,4)r(1,5)r(2,4)r(2,5)r(3,4)r(3,5)］T。下面只需把编码后的消息发送给各终端，然后终端利用自己的边信息解得期望消息，即相当于一个广播信道模型。

　　2.2BC阶段

　　在BC阶段要发送编码后的消息，需要考虑如何设计各个消息的波束成形矢量。为了尽可能地避免非期望消息带来的干扰，考虑如MAC阶段的式(4)，设计信道对齐向量来对齐信道：

　　span(d1,4H1,r)=span(d4,1H4,r)=span(fr(1,4))(7)

　　由式(4)的推理过程，容易理解此式是成立的，详细过程不再赘述。对齐所有的信道以后，可以得到：Fr=［fTr(1,4)fTr(1,5)fTr(2,4)fTr(2,5)fTr(3,4)fTr(3,5)］T，然后定义r(i,j)=Fr/fr(i,j)，表示在Fr中去除fr(i,j)后的矩阵。因为r(i,j)是一个5×6的矩阵，存在零空间，那么就可以得到其零向量pr(i,j)null(r(i,j))。然后以pr(i,j)作为叠加消息r(i,j)的波束成形矢量，以Pr=［pr(1,4)pr(1,5)pr(2,4)pr(2,5)pr(3,4)pr(3,5)］作为消息向量的波束成形矩阵。而信道对齐向量构成的矩阵为终端处的过滤矩阵，以终端1为例，它的过滤矩阵为D1=［dT1,4dT1,5］T。那么由此可知终端1收到的信号可表示为y1=H1,rPrr+n1，由于使用了过滤矩阵，则可将其转化为：

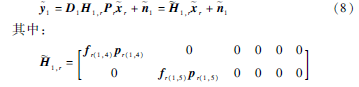
　　这样在终端1可以得到期望的叠加消息r(1,4)和r(1,5)，然后利用其自己的消息即可得到期望消息x1,4和x1,5。其他的终端也用类似方法得到其期望消息。

3天线配置条件

　　假设任意两个相互通信的终端，每次通信的消息数为d，则有Ai≥2d，Aj≥3d，那么由割集理论可知，总的自由度：

　　dsum≤2min∑3i=1Ai,AR,∑5j=4Aj=2AR=12d

　　由此可知2AR=12d是一个上界，并且：

　　d14+d15+d24+d25+d34+d35=6d=AR

　　又由2.1节分析可知，应有：

　　di,j≤Ai+Aj－AR

　　所以可得：

　　AR≤67(Ai+Aj)（9）

　　由上面的分析可知，各终端与中继的天线数应该满足式（9）条件。

　　但是，当终端数量较多时，需要通信的消息数很多，就要求中继和终端的天线数急剧增加，而这在实际应用中并不容易实现，除非采用大规模MIMO技术。考虑到空时转换，下节介绍了基于时间扩展的方案来缓解这一问题。其基本思想是通过通信时隙的增加来降低对天线数的要求，基本方法仍然是信号对齐的方法。此方案尽管降低了单位时隙的自由度，但更容易实现。

4时间扩展方案

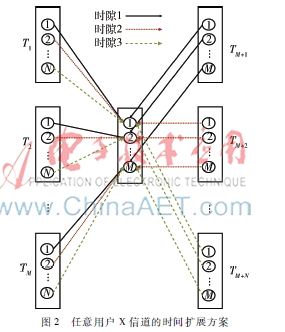
　　图2所示是一般的双向中继的M×N X 信道模型。左侧M个终端都装备有N条天线，而中继和右侧的N个终端都有M条天线，整个过程在N个时隙内完成2MN个消息的传输。　

　　4.1MAC阶段

　　以第一个时隙为例，在第一个时隙，右侧终端TM+1分别向左侧M个终端各发送一个消息xi,M+1(i=1,2,…,M)，共M个消息。而左侧的M个终端Ti(i=1,2,…,M)分别发送它们的第一个消息xM+1,i给右侧的终端TM+1。

　　其他时隙也类似，那么在时隙t，中继收到的消息为：

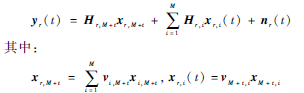
　　中继收到了2M个消息，要把它们对齐在M个维度中就要使得Hr,M+tvi,M+t=Hr,ivM+t,i成立，又因为Hr,M+t和Hr,i分别是M×M和M×N的，所以vi,M+t和vM+t,i是容易得到的。

　　4.2BC阶段

　　如前面第2节所分析，这里中继再把2M个消息对齐到M个维度后，得到网络编码后的消息，然后发送给各个终端。

　　这里右侧终端有M条天线，与中继的通信相当于点对点的通信，自然可以解得所有的消息。而对于左侧的M个终端，每个终端只有一个期望信号，与中继组成一个广播信道，也可以得到其期望的叠加消息。最后，每个终端利用自己发出的消息即可得到期望消息。

　　所以在每一个时隙里面，右侧的一个终端解得了M个消息，左侧的M个终端都分别解得了一个消息，加起来也是M个消息。那么在N个时隙里面，整个网络共实现了2MN个消息的通信。

5结论

　　针对双向中继3×2X信道，详细分析了信号对齐方案的实现过程，并且得到了较高的自由度，同时也分析了该方案的限制条件。结合实际应用，对于一般多用户的X信道，本文提出了时间扩展的方案，通过增加时隙数来降低对天线数的需求。如何在保证高自由度的同时，进一步降低对终端天线数的要求将是下一步的研究重点。

参考文献

　　［1］ JAFAR S, SHAMAI S. Degrees of freedom region for the MIMO X channel ［J］. IEEE Transactions on Information Theory, 2008,54,（1）：151170.

　　［2］ SUN H, GENG C, GOU T, et al. Degrees of freedom of MIMO x networks: spatial scale invariance, onesided decomposability and linear feaibility［C］. IEEE International Symposium on Information Theory Proceedings, 2012： 20822086.

　　［3］ SHANNON C E. Twoway communication channels［C］. Proc.4th Berkeley Symp. on Math, Statist, Probab, 1961: 611644.

　　［4］ LEE N, LIM J B, CHUN J. Degrees of freedom of the MIMO Y channel: signal space alignment for network coding［J］. IEEE Transactions on Information Theory, 2010, 56(7): 33323342.

　　［5］ 范乐园,唐加山.半可逆MIMO信道多值信号盲检测［J］.微型机与应用,2014,33(12):5760.

　　［6］ 刘国华,黄洪琼,吴程,等.MIMO系统的正则块对角化迫零矢量预编码设计［J］.微型机与应用,2015,34(10):6466,69.

　　［7］ ZHANG S, LIEW S C, LAM P K, et al. Physical layer network coding［J］. Acm Mobicom,2007,24(23): 21662168.