刘畅安1，胡芳仁1, 2，刘昕1

　　（1. 南京邮电大学 光电工程学院，江苏 南京 210023； 2. 南京邮电大学 Peter Grüenberg中心，江苏 南京 210023）

　　摘要：在相干光通信中，利用载波相位恢复算法来减小由于激光器线宽和ASE噪声所造成的相位偏移。对载波相位恢复算法进行了研究，在此基础上提出了利用小波变换中的小波分解和小波重构的方法来减少相位噪声，通过结果比对选取最佳分解次数，并对此方法进行迭代，以提高去噪性能。小波分析中用到的小波系数没有唯一性，仿真中选取了不同的基小波并对结果进行分析。结果表明通过小波变换算法能够有效地对激光器的初始相位偏差进行恢复，为载波相位恢复提供了一种新的解决办法。

　　关键词：相干光通信；载波相位恢复；小波变换

0引言

　　相干光通信的接收模块采用了较大功率本地震荡(LO)激光器，与传统光通信相比，相干光通信有着更高的检测灵敏度，适用于更高速的传输速率［1］。相干光通信系统对相位噪声和光纤色散等因素导致的系统失真非常敏感，应当在接收中应用数字信号处理(DSP)技术在电域实现补偿［2］。载波相位恢复算法作为数字信号处理中的一部分，针对由于激光器线宽和ASE噪声产生的相位噪声进行补偿，使接收到的相位接近初始相位。常用的载波相位恢复算法有M次幂算法、预判决算法、盲相位搜索算法等［3］。

1小波变换

　　1.1小波分析处理信号

　　传统的载波相位恢复算法简单可行，但是恢复精度一般，并且对于激光器初始相位偏差的容忍度较低，如果初始相位偏差过大，会增加系统的误码率。小波变换具有低熵性、多分辨率性、去相关性、选基灵活性等特点，可根据信号特点选择合适的小波［4］。基于小波变换的相位恢复可以对激光器初始相位进行有效的补偿，解决高精度与时延的矛盾。

　　1.2小波分解和小波重构

　　小波是均值为零的一类波形，对于任选函数f(t)∈L2(R)，连续小波变换为：

　　连续小波变换具有尺度a和平移t两个参数，频率ω尺度越小对应频率越高，离散小波分解将小波基函数ψa,b=|a|－12ψ(t－ba)的a、t限定在一定离散点上取值，可得离散小波变换函数：

　　信号小波包分解算法为：由dj+1,ni，求dj,2ni和dj,2n+1i。

　　信号的重构分为信号的小波重构和信号的小波包重构，通过小波变换的方法，可以将信号分解成两部分。第一部分是近似系数，表现的是信号的低频部分，具有较低的时间分辨率和较高的频率分辨率；第二部分是细节系数，表现的是信号的高频部分，具有较高的时间分辨率和较低的频率分辨率。分解的层数应当适中，分解次数过多反而会使SNR下降。因此，在选取不同的小波基时，有不同的最佳分解次数［5］。

2基于小波变换的载波相位恢复算法

　　2.1接收端的信号

　　QPSK信号经过前端预处理、色散补偿、均衡等技术之后，单偏振态上第n个接收符号可以表示为［6］：

　　其中，k表示第k个抽样时间的间隔［kT,(k+1)T］；PS为信号功率；θn(k)∈［0,π2,π,3π2］为调制相位；φn(k)为激光器相位噪声，服从维纳分布，所以两个相邻符号之间的相位差φn－φn－1服从均值为0，方差为σ2=2π(Δω)T的高斯分布，其中Δω为发送端激光器与本地震荡激光器的整体线宽；n(k)表示ASE噪声，是一种高斯白噪声。由于相位噪声的影响，QPSK信号星座图会出现旋转，导致相邻符号之间互相干扰，当干扰超过一定的临界点时，会导致信息出现错误判决的可能［7］。

　　2.2基小波选取和特点

　　小波函数ψ(t)具有多样性，小波分析在应用中的重要问题就是最优小波基的选择问题，使用不同的小波基分析同一问题会有不同的结果，目前主要是通过用小波分析方法处理信号的结果与理论结果的误差来判定小波基的好坏，由此决定小波基［6］。

　　db系列小波在时域是有限支撑的，即Ψ(t)长度有限。在频域ψ(ω)的ω=0处有N阶零点。Ψ(t)和它的整数位移正交归一，即∫ψ(t)ψ(t-k)dt=δk。小波函数Ψ(t)可以由所谓“尺度函数”φ(t)求出来。尺度函数φ(t)为低通函数，长度有限，支撑域在t为0~(2N-1)范围内。

　　2.3小波变换去除相位噪声方案

　　在相干光接收机接收到的信号中，包含了激光器线宽和相位偏移产生的相位噪声以及自发辐射噪声。针对这些噪声，提出了一种基于选取小波包进行分解和重构，将ASE噪声和相位噪声分别滤除的结构系统，其原理如图1所示。先将信号整体进行小波分解和重构，消除由于ASE噪声带来的加性噪声。之后对信号相位进行小波分解和重构，滤除相位噪声，并对此过程进行迭代，提高去噪性能。最后求得信号幅角并对延时之后的原信号进行补偿，完成载波相位估计。

3仿真结果与分析

　　仿真中，采用了40 Gb/s的QPSK传输系统，其中，激光器初始相位为零，信噪比定义为QPSK信号的功率与ASE噪声的功率在电域的比值。选取了不同的小波基，在不同的阈值条件下分析对比去噪性能。在使用db8小波时，多次分解后波形相对平滑，仿真中经过6层分解，去噪前后得到的信号源对比如图2所示。

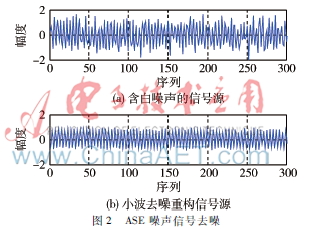
　　从图2可以看出，ASE噪声作为加性高斯白噪声被很好地去除，经过小波分解和小波重构后的信号源幅度更加稳定。由于使用QPSK调制方式，信号的相位应当稳定在（0，π2，π，3π2），在激光器线宽的影响下，会产生相位偏差，通过仿真（如图3所示）可以看出，序列中许多的点相位幅度发生了明显的偏移，当偏移的幅度超过一定的阈值时，会造成接收时的误判，使得系统误码率增加，降低系统可靠性。经过小波分解重构并迭代后的信号相位如图4所示，从图中可以看出序列中各个点位基本恢复到发射机的初始相位附近。其中，可以最直观地看出，3π2相位上的点基本接近它的数值4.71并且幅度稳定无突变，证明了小波变换可以有效地恢复发射端的初始相位。　

　　选取了不同的小波基Daubechies(dbN)、Biorthogonal(boirN)、Coiflet(coifN)、Symlets(symN)在同一系统中，其中N为小波阶数，应用本文中的去噪方案，得到的误码率信噪比如图5所示，在信噪比增大的同时，尤其是OSNR在8 dB~16 dB时，利用小波变换的载波相位恢复算法可以有效地改善系统误码率。对比不同的小波基，可以看出选用db8.4时性能最佳。　

　　在不同的小波基下，分解次数的多少影响着系统性能，在现有系统中，针对db8.4小波基，对不同分解重构次数后的系统性能进行比较，仿真结果如图6所示，图中N为分解次数，结果表明分解层数为6时，系统性能最好。　　

4结论

　　针对激光器线宽和ASE噪声造成的相位偏移，提出了一种利用小波分解和重构进行去噪的系统，通过两次小波变换，分别滤除系统中的ASE噪声和相位噪声，通过多次迭代优化系统性能。改进了普通的盲估计算法，在不增加过多的算法复杂度的同时，提高了相位恢复精度。仿真结果表明，在本系统中应用db8.4小波，分解层数为6时，系统性能最佳。

参考文献

　　［1］ GORSHTEIN A, DAN S.Advanced modulation formats and digital signal processing for fiber optic communication ［C］.International Conference on Transparent Optical Networks, ICTON 2010 Shanghai, China,2010,123(8):13.

　　［2］ SHARIF M, KAHN J M. Variablebandwidth super channels using synchronized colorless transceivers［J］. Journal of Lightwave Technology，2014,32(10):19211928.

　　［3］ 袁卫文,蒯震华,吕振彬,等.基于LED的高速可见光通信系统研究［J］.微型机与应用,2014,33(19):14,11.

　　［4］ 吕媛,秦祖军,梁国令,等.融合数字累加平均和小波变换的信号降噪测试［J］.微型机与应用,2015,34(7):1315,19.

　　［5］ ZHANG S, YU C, KAM P Y, et al.Parallel implementation of decisionaided maximumlikelihood phase estimation in coherent Mary phaseshift keying systems［J］.IEEE Photonics Technology Letters, 2009,21(19):14711473.

　　［6］ 张德丰.MATLAB小波分析 ［M］.北京：机械工业出版社2011.

　　［7］ Wu Nan, Wang Hua, Li Zhixin, et al. Performance analysis of codeaided iterative hard/soft decisiondirected carrier phase recovery［C］.Global Communications Conference 2012, California, U.S.A,2012:38133818.