张大勇1,凌强1,计炜梁1,张俊斌2,徐酉亮2,熊远波2,吴艺英2
(1.中国科学技术大学 自动化系,安徽 合肥 230027; 2.白城兵器实验中心 轻武器部,吉林 白城 137001)
摘要:针对周期噪声与窄带噪声,基于DSP硬件平台,进行主动降噪系统设计与实现。主要工作为次级通道辨识、对算法定点化处理和基于DSP的实时降噪实现。所提出的定点化方法大大提高了定点DSP的运算速度,保证了降噪的实时性。其中降噪程序采用自适应算法中的前馈滤波X最小均方算法,DSP采用德州仪器公司的16位定点DSP TMS320VC5509A,使用TLV320AIC23B作为音频处理芯片,取得了明显降噪效果。
关键词:主动降噪;滤波-X-最小均方算法;定点化
0引言
一直以来,噪声污染都是各国十分关注的问题,同时它还是一个越来越严重的环境污染问题。交通噪声、工业噪声、建筑噪声等给人的生理和心理健康带来严重危害。这些噪声使人听力下降、易于疲劳、注意力下降、工作效率降低。因此,在噪声越来越严重而人们越来越追求身体健康与生活质量的情况下,对噪声的降低,在理论研究和工程实践中都将具有广泛的研究价值和广阔的市场前景。
传统的噪声控制方法主要有吸声、隔声和使用消声器等被动降噪(Passive Noise Control)方法[1],其本质是利用声波与材料的机械作用,使声能变为热能等其他形式的能量以减少噪声。随着信号处理技术和电子技术的高速发展,主动噪声控制(Active Noise Control)有了明显的进展[2]。其原理是根据2个声波相消性干涉或声波辐射抑制的方法,通过人为地制造1个控制声源 (次级声源),使其发出的声音与原来的噪声源(初级声源)辐射噪声大小相等、相位相反,使两者作用结果互相抵消,从而达到降噪的目的。本文即采用主动降噪思想,使用前馈滤波X最小均方(FXLMS)算法[3 4],并借助DSP平台构造一个主动降噪系统。
本文首先通过DSP平台产生白噪声对次级通道进行辨识,然后对浮点程序进行定点化处理,最后通过扬声器产生反噪声来抵消外界噪声。针对单频噪声和窄带噪声进行降噪处理,能够在C55x系列DSP平台上实现实时性;而且通过对浮点算法进行定点化处理,大大提高了在DSP平台上的运算速度;通过提高采样率,可以对最高7 kHz的高频噪声进行降噪,以适应噪声可能存在的变化。
1次级通道辨识
前馈X-滤波最小均方算法(FXLMS)算法即在基本的LMS算法的基础上考虑了次级通道S(z)的影响。如图1所示,次级通道指从产生声音信号并通过扬声器输出,到通过拾音装置采集并获得声音信号的通道S(z)。原始噪声d(n)叠加在自适应滤波器输出的噪声抵消信号y(n)上,误差信号e(n)被误差麦克风检测到。但y(n)到e(n)的声音次级通道函数S(z)会改变噪声抵消信号y(n),因此,需要对次级通道进行建模,构造S^(z)对次级通道进行补偿。

具体的次级通道包括扬声器中的D/A转换器、重构滤波器、功放,扬声器到拾音装置声器之间的通道,拾音装置中的误差传声器、前置放大、抗混叠滤波器以及A/D转换器。设定次级通道为30阶,为了更准确地辨识次级通道,本文根据最小均方算法进行运算。

如图2所示,次级通道的辨识过程如下。
(1)通过DSP平台产生白噪声y(n)并由音频编解码芯片aic23读取,然后通过抵消扬声器发出白噪声。
(2)通过抵消麦克风采集步骤(1)中抵消扬声器发出的白噪声信号。
(3)利用步骤(1)中的白噪声信号计算自适应滤波器的输出信号r(n),求取公式如下:

式中u(n)表示步骤(1)产生的白噪声信号序列,si(n)表示自适应滤波器系数,n为当前时刻,M为滤波器阶数,i为滤波器的阶数序号。
(4)计算误差信号,其求取公式如下:
e′(n)=v(n)-r(n)(2)
式中v(n)为误差麦克风采集到的声音信号,r(n)为步骤(3)中自适应滤波器的输出。
(5)利用最小均方准则更新自适应滤波器的系数,其求取公式如下:
si(n+1)=si(n)+μe′(n)u(n-i),
i=1,…,M-1(3)
式中:迭代步长μ取值0.05,滤波器阶数M取30阶。
(6)判断迭代次数是否大于T(T取10 000)次,当迭代次数大于T时,停止迭代,完成对次级通道的辨识,此时就得到了次级通道的系数。
2对浮点程序定点化处理
现有的DSP处理器中,无论从运算速度还是设备成本看,定点处理器较浮点处理器都有一定的优势[5],因此本设计采用了C55x系列的16 bit定点DSP TMS320C5509A。但是由于定点DSP处理浮点数据比较慢,因此对浮点程序进行了定点化处理。定点化可以直接着手进行,也可以在完成浮点算法的基础上对降噪程序进行改造,本设计采用后者。
采用定点数表示实际的浮点数,浮点数和定点数的转换公式如下:
浮点数(X)转换为定点数:
XQ=(int)X*2Q(4)
定点数(XQ)转换为浮点数:
X=(float)XQ*2-Q(5)
对浮点算法定点化时,加减法的运算规则不变,乘法运算时要将乘积除以2n,而乘除法运算时要将被除数乘以2n,由于对2n进行乘除运算均可以用移位运算替代,因此可以大大提高运算速度。
不同的Q格式所表示的数的范围不同,精度也不同。Q越大,数值范围越小,但精度越高。例如,Q0(Q=0)的数值范围是-32 768~+32 767,其精度是1,而Q15的数值范围为-1~0.999 969 5,精度为1/32 768=0.000 030 51,因此数据范围和精度是一对矛盾。
如图3所示,本设计中针对浮点程序的定点化处理流程如下。

(1)定标方式选取为Q15。
(2)利用式X15=(int)X*215将已知的浮点数据转换为定点数据。所谓已知的数据是指能直接采集到的输入信号(如采集麦克风采集到的噪声信号,误差麦克风采集到的误差信号),以及一些需要设定的参数(如迭代步长μ)。
(3)将需要计算才能得到的浮点数据求取公式进行定点化改造。例如浮点算法中e′(n)的求解公式为:
e′(n)=v(n)-r(n)
定点化后e′(n)的求解公式为:
e′15(n)=v15(n)-r15(n)(6)
r15 (n)为反噪声信号r(n)的定点化形式,v15 (n)为误差麦克风采集的误差信号v(n)的定点化形式,可由步骤(2)求得,即:
v15(n)=(int)v*215(7)
(4)用定点化算法对次级通道进行再次辨识并测得次级通道的整形系数。通过DSP平台产生白噪声,并通过噪声抵消扬声器输出,对次级通道进行辨识,得到次级通道整形系数。
(5)判断数据精度是否满足要求。将步骤(4)中所测的次级通道的系数与浮点算法得到的系数进行比较。如果次级通道的整形系数除以215后与浮点系数的误差在-0.003~0.003之间,则数据精度符合要求,定点化结束。如果不满足这个条件,就需要改变定标格式对定点化进一步改进,进入步骤(6)。
(6)使用Q16~Q31定标方式,并进入步骤(2)再次进行定点化改造。
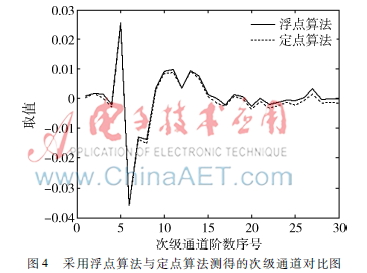
采用浮点算法与定点算法测得的次级通道对比图如图4所示,图中实线表示浮点算法得到的次级通道的浮点系数。由于定点算法中次级通道采用的是Q15格式,因此虚线是定点算法学习到的系数除以215之后的数值,次级通道设定为30阶,采样率为1 kHz。可以发现,两条曲线几乎重合,它们的最大误差是0.001 9,在-0.003~0.003之间。因此采用Q15定标方法的定点算法后,精度满足要求。
3利用扬声器产生反噪声来抵消外界噪声
定点程序的精度满足要求时,即开始进行降噪的阶段。对于外界单频与窄带噪声,通过抵消扬声器发出反噪声,可以达到良好的降噪效果。
如图5所示,降噪实现过程如下。
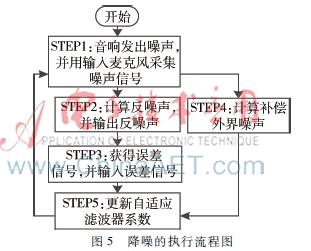
(1)由音响输出噪声并通过采集麦克风采集该噪声信号。
(2)利用步骤(1)采集的噪声信号计算需要的反噪声信号y(n),并利用抵消扬声器发出,其求取公式为:

式中x(n)为在n时刻采集到的外界噪声,wi(n)为自适应降噪滤波器在n时刻的系数,N为自适应降噪滤波器的阶数。
(3)由误差麦克风采集误差噪声信号e(n)。
(4)计算利用步骤(1)中采集到的噪声信号经过次级通道进行补偿后的值,其求取公式为:

式中ci(n)次级通道的系数,x(n)为在n时刻采集到的外界噪声,M为该自适应滤波器系数。
(5)利用最小均方准则更新自适应降噪滤波器的系数wi(n),其求取公式如下:
wi(n+1)=wi(n)-μ*e(n)*x′(n-i)
i=0,…,N-1(10)
式中e(n)为步骤(3)中采集得到的误差噪声信号,i为滤波器阶数序号,μ为迭代步长,x′(n)为步骤(4)中得到的噪声信号的补偿值。通过不断调节自适应滤波器系数滤就可以对外界噪声进行实时降噪处理。
4实验结果

利用音响发出7 kHz音频作为外界噪声,利用CCS软件的Graph功能对得到的数据进行作图并截图,采样率设为16 kHz,结果如图6和图7所示。由图6与图7可以看出,降噪前噪声幅值为1 300,降噪后最大值为300,换算为降噪比为:
20lg(1 300/300)=12.7dB
降噪效果比较明显。同时,噪声在开启降噪到迭代250次稳定,需要的时间是:
250/16000=0.015 625 s
由于人耳的反应时间是0.1 s左右,因此降噪可以取得很好的实时效果。
5结论
本文利用前馈FXLMS算法进行ANC程序设计,提出了一种针对浮点FXLMS算法定点化的方法,通过在德州仪器公司的定点DSP C5509A上实施,大大提高了定点DSP的运算速度,使降噪可以具有实时性;同时,还可以对高频噪声取得良好的降噪效果。为了增强系统的性能,在今后的工作中可以考虑限制自适应滤波器系数的波动范围[4],或者采用变步长的改进算法[6 7],以增强系统的鲁棒性。
参考文献
[1] 周亚丽. 有源噪声与振动控制[M]. 北京:清华大学出版社, 2014.
[2] 陈克安. 有源噪声控制[M]. 北京:国防工业出版社, 2003.

