顾天1,李晓丽1,赵曙光1,郑鹏远2
(1.东华大学 信息科学与技术学院,上海 201620; 2.上海电力学院 自动化工程学院,上海 200090)
摘要:网络系统的规模不断扩展,趋向于庞大复杂化。文章针对系统内部信息传递所带来的控制滞后等问题,在网络系统能控的研究基础上引入能控性指数的概念,用以描述网络系统能控的性能指标;基于二分图提出算法获得网络系统能控性指数,并提供每个控制量相应的控制链,为后续划分大规模网络系统的节点群等研究工作提供科学依据。
关键词:网络系统;二分图;能控性指数
0引言
随着计算机技术的飞速发展,出现了越来越多规模庞大且结构复杂的网络,其通常具有空间分布式特征,例如跨区域的电力网、纵横交错的交通网等。对网络中若干节点施加控制以实现整个网络能控,对网络系统的可控性进行分析,可望在进入定量研究前先得到全局的指导信息[1] ,有助于理解各控制量对网络系统的影响。目前网络系统的可控性是指在不限制控制步数的情况下,通过施加控制量使其可控,但随着网络规模的不断扩大,网络系统的各个组成部分彼此间传递信息或状态会带来控制作用滞后等问题[2]。通过基于能控性指数的算法研究可以将大网络系统分散化进行控制,缩短了控制过程。
1问题描述及判据
大规模网络系统具有极其复杂的结构和不稳定性。针对高维性、非线性的大系统,研究其可控性问题十分复杂,可以将其转化为在一定范围内按不同工作点线性化所得的线性系统,进而分析转化后的线性系统是否可控[1] 。考虑由n个节点构成的线性时不变网络系统:
(t)=Ax(t)+Bu(t)(x∈Rn,u∈Rm)(1)
令G(α,β)为一个有向图用以描述网络,节点集α={1,2...n},边集β=α×α,一条边(i,j)∈β表示节点i可达节点j,但反之不成立。由i向j所建立的联系表示为aij,无法建立联系则为0。j为i的邻接节点,定义Ni为i的所有邻接节点的集合,j∈Ni。n×n维常值矩阵A用以描述网络各节点间的关联情况;B为n×m维常值输入矩阵,表示控制器对节点的影响[3],若对节点j直接施加控制器uj则表示为bj。
定义1:系统(1)可控的充要条件:
rank[B,AB,A2B...An-1B]=n(2)
网络系统可控表明其可由任意初始状态受控制器驱动到达任何所需的最终状态[4]。其中矩阵An-1B本质上体现了从控制器出发在n-1步路径内与网络系统所有节点建立了联系,根据定义1引入网络能控性指数μ,对于n维连续时间线性时不变系统,能控性指数μ定义如下:
定义2:系统(1)k步可控的充要条件:
gr[B,AB,A2B...AkB]=n(3)
满足式(3)的k的最小值即为能控性指数μ。
图1为由4个节点构成的网络系统,对其进行分析。
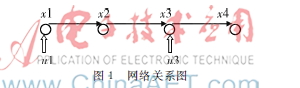
其中常值矩阵A、B为:

分析发现gr[B,AB,A2B,A3B]=4,符合定义1与定义2,表明该网络系统可控,也可称之为3步可控。同时gr[B,AB]=4,符合定义2,而gr[B]<4,则满足条件的k的最小值为1,即能控性指数为1,控制链如图2所示。

2算法
将一个图的顶点划分为两个不相交集U和V,使得连边分别连接U、V中的顶点,若存在这样的划分则此图就是一个二分图,而边数最多的匹配方法即为最大匹配[5]。通过最大匹配能解决很多实际问题,如棋盘走法、配对问题等。匈牙利数学家Edmonds对二分图的最大匹配进行研究并得到一种普适性的匈牙利算法。
2.1匈牙利算法
以图3为例介绍匈牙利算法的基本思想。
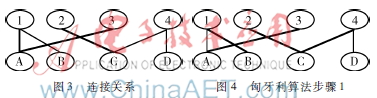
首先从1开始匹配:1-A,2-C,3-A,如图3加粗路线,此时由于A已匹配给1,因此将1-A转变为1-B,从而成功匹配3-A,如图4所示。
1继续匹配4,4-C,如图4所示。此时由于C已经匹配给2,为了形成更多的匹配边,因此将4-C转变为4-D。最终图5匈牙利算法步骤2最大匹配方案为1-B、2-C、3-A、4-D,如图5所示。

2.2算法Aci
研究网络系统可控性时,可以将网络表示为二分图,利用最大匹配理论匹配尽可能多的边,得出为使网络可控的一种控制器选取方案,而本文基于可控网络分析匹配方案以获取能控性指数。
假设网络系统如图6所示。

通过匈牙利算法可知对节点1、3、5、9施加控制可使该网络可控,但分析控制方案时会出现图7所示匹配方式:
由控制器u5控制的节点群5-6-7-2-8形成了一条控制链,但相比于1、3-4、9-10,该条控制链显得较长,易影响控制作用。
在已知网络可控的基础上,从各控制量出发,根据节点间的可达关系逐步匹配节点形成或长或短的控制链。将一条控制链看作一个子系统,当整个系统划分成若干子系统后,若其分别为k1,k2,…kn步可控,定义其中最大值为kmax,则整个大系统称为kmax步可控。kmax需尽可能小,当其取值最小时即为能控性指数μ。
以控制器直接控制的节点i为起始点,同时进行匹配。由网络可控可知每个节点都必存在于匹配边中,因此若匹配完成后仍有节点未被匹配,则必须改变某节点的匹配方式,直至所有节点均被匹配。
能控性指数算法Aci描述如下:
(1)列出所有根节点i(1≤i≤n);
(2)λ:根节点i的数目,设置k=0;
(3)重复步骤(4)~(6);
(4)匹配i的可达节点j(i-j),j∈Ni,若j出现重复则改变前者匹配方式,j的数目为η,k=k+1,λ=λ+η;
(5)令j为新的根节点,匹配其可达节点;
(6)当η=0,λ≠n,节点σ未匹配(δ可达σ),退回δ所在步骤,改变其匹配方式为δ-σ,从该步骤开始继续向下匹配;
(7)直至λ=n,n为网络节点数目;
(8)所有节点已存在于匹配边中,μ=k。
3仿真与结论
利用二分图描述图6所示网络,如图8所示,箭头表示始端节点可达末端节点,例如1指向2表示节点1可达节点2。
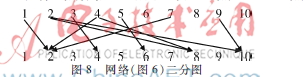
分析图6网络,n=10,k=0,起始点为1、3、5、9,λ=4,第一步如图9所示。

匹配节点为2、4、6、10,η=4。此时λ=8,k=1,第二步如图10所示。
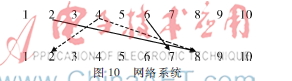
匹配节点为8、7。其中4-2,2在第一步就已匹配(舍去),转变为4-8,而此步骤已将8分配给了2,改变匹配方式2-10,而10在第一步就已匹配(舍去),因此2向下不可再匹配,η=2。此时λ=10=n,所有节点已存在于匹配边中,k=2,μ=2。
最终匹配方式如图11所示,控制链为:1-2;3-4-8;5-6-7;9-10。同时可验证gr[B,AB,A2B]=10,k的最小值为2,即能控性指数μ=2。

以图12网络系统为例,可控性指数μ=5,通过匹配边将原本关联复杂的网络分散化,获得各条结构简单明了的控制链,使得控制作用更有效。

4结束语
本文引入网络系统能控性指数的概念并给出能控性判据,在此基础上提出算法Aci获得能控性指数及相应的控制链,缩短了控制过程和时间。在实际网络如电网中,大量节点具有固定的匹配方式,这样就能为分析网络的k步可控性节省大量时间,同时研究各个控制器所控制的节点群,可以明显地从复杂的网络中得到各条清晰的控制链,以各控制器为起始点,只需抓住这个起始点将其从网络中抽出便可获知该控制器依次控制的各个节点。对于研究某些实际网络模型有很大的参考价值,并可反过来服务于研究控制器的选取。
参考文献
[1] 席裕庚.动态大系统方法导论[M].北京:国防工业出版社,1988.
[2] 李健勇,罗永平,黄道颖,等.网络控制系统时延分布分析与建模[J].郑州轻工业学院学报(自然科学版),2014,29(4):5053.
[3] Liu Yangyu, SLOTINE J J, BARABA′SI A L. Controllability of complex networks[J]. Nature, 2011,473(12):167173.
[4] 郑大钟.线性系统理论[M].北京:清华大学出社,2011.
[5] 邵长城,张锡哲.复杂网络可控性分析与驱动节点集拓扑性质研究[D].沈阳:东北大学,2012.

