李银1,2,何强1,2,乔龙辉1,2
(1.重庆邮电大学,重庆400065;2.重庆信科设计有限公司,重庆400065)
摘要:针对SIFT算法对大角度视角变化下特征提取鲁棒性不强的弱点,引入了一种完全仿射不变的图像特征匹配算法—ASIFT。ASIFT算法不仅继承了SIFT算法的尺度、旋转和平移的不变性,并且在此基础上增加了两个空间特征描述参数:经度和纬度,从而定义出度量仿射形变的两个参量绝对倾斜t(absolute tilt)和过渡倾斜τ(transition tilt),模拟相机光轴变化,实现完全仿射不变。一种双分辨率(two-resolution)加速方法的提出,使ASIFT算法的复杂度约为SIFT的2倍。
关键词:特征匹配;仿射不变;过渡倾斜;绝对倾斜;双分辨率;SIFT;ASIFT
0引言
图像匹配旨在建立出现在不同的图像相似对象之间的对应关系,已在许多计算机视觉和图像处理方面得到应用,例如图像识别、三维重建、目标跟踪、机器人定位等。目前国际上最先进的图像匹配算法通常由检测器和描述符两部分组成,根据不变特性可以分为:平移和旋转不变特性的Harris角点检测器[1] ;旋转和尺度不变的HarrisLaplace、HessianLaplace和DoG(差分高斯)区域检测器[23];仿射性不变的基于双极线的区域检测器MSER[4]。这些方法通过归一化局部区域、部分区域或者水平线修补程序可以形成仿射变换,当归一化这些参量使其成为标准对象时,仿射变换的效果就会消除。LOWE D G提出了尺度不变特征转换SIFT[56],是完全尺度不变的唯一方法,由于SIFT没有覆盖整个仿射空间,它的性能在视角变化的情况下迅速降低,因而不具有完全仿射性。
ASIFT算法建立模型增加了经度和纬度两个参数,模拟相机轴方向和尺度变化,并归一化旋转和平移,实现了完全仿射不变,但相应的复杂度会大大增加。它是一种双分辨率方法,具有单一的SIFT算法大约两倍的复杂性。经过实验发现,ASIFT算法能够很好地处理视角变化的图像仿射特征匹配,验证了仿射不变性。因而ASIFT算法匹配在各种复杂情况下的图像识别领域都有广阔的应用前景。
1仿射变换模拟
1.1仿射相机模型
通过仿射平面变换能模拟拍摄视角变化所产生的图像形变,这种模型提供对象的边界是分段光滑的,因此,一种摄像机运动图像变形模型[7]表示如下:
μ(ax+by+e,cx+dy+f)
其中,A=ab
cd为线性平面的正行列式,可以分解为:
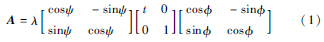
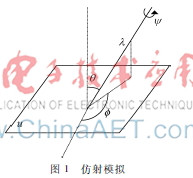
图1仿射模拟记A=λR(ψ)TtR(),其中λ>0,λ是A的决定因子,R(ψ)表示平面旋转ψ角, Tt(t>1)指倾斜。图1是对式(1)的摄像机运动解释:和θ=arccos1t是指相机的视角,ψ参数化相机旋转。在这个仿射模型中,相机远离平面物体,从正面开始,平行于对象平面的相机运动会引起图像旋转,具有法线和光轴的平面与固定的垂直平面形成的夹角称为经度;光轴与平面u的法线之间夹角θ称为纬度;定义倾斜t=1cosθ,相机可绕其光轴旋转(旋转参数ψ),相机通过变焦参数λ前后移动。
1.2视角变换下的仿射模型

式(1)定义了绝对倾斜(absolute tilt)t,它表示相机从正面到斜视图的图像形变率,用来量化图像之间的倾斜量。图2绝对倾斜示例图图2、图3描述了绝对倾斜与过渡倾斜的不同。
图3过渡倾斜示例图图2中相机在移动的过程中保持过渡倾斜与绝对倾斜同步,即经度不变=′,纬度θ=30°,θ′=60°,绝对倾斜t=1cosθ=23,t′=1cosθ′=2,过渡倾斜τ(μ1,μ2)=t1′t2=3。
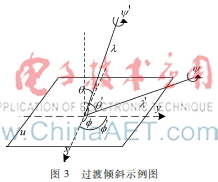
图3表示在正交方向上倾斜:=′+90°,μ1与μ2之间的过渡倾斜可表示为:τ(μ1,μ2)=t′t,取θ=60°,θ′=75.3°,t=2,t′=4,τ(μ1,μ2)=t′t=8,可见两幅图的正常绝对倾斜会产生较大的过渡倾斜。因此在实际应用中绝对倾斜t只能取到6,对应的纬度角θ≈80.5° ,过渡倾斜τ可达到36。
2ASIFT算法
SIFT算法思想是结合模拟和归一化。SIFT检测器对目标图像归一化旋转、平移,模拟尺度缩放,因此SIFT是唯一的完全的尺度不变方法。ASIFT算法在SIFT的基础上进行了改进,模拟尺度、经度和纬度3个参数,并且归一化旋转和平移,由此完成了对整个仿射空间的模拟,实现仿射不变性,相关证明参见参考文献[8]。图4形象地表示了对ASIFT算法的概述,其中正方形A、B代表匹配图像,模拟产生图像由周围的平行四边形表示,从而完成了模拟因相机光轴方向变化所产生的形变。由于ASIFT特征提取过程复杂,计算量大,一种双分辨率(two-resolution)的提出将进一步减少SIFT算法的复杂性,大约是SIFT的2倍。

2.1ASIFT算法过程
(1)经度纬度采样:由相机光轴产生的形变取决于两个参数:经度和纬度θ,过渡倾斜τ=1cosθ,因此纬度可以按照等比数列t=1,a,a2…an进行采样,考虑到精确性和稀疏性,a=2为最优选择, n可以取到5甚至更高,这样过渡倾斜τ可以达到36甚至更高;经度对每个倾斜取等差数列0,bt,2bt…kbt,取b=72°使数列的最后一个整数kbt<180°。
(2)确定模拟图像:由(1)中采样得到的和tt=1cosθ,模拟图像表示如下:
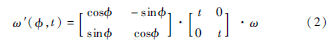
其中ω为输入图像,以每组和θ采样通过式(2)得到一组模拟图。
(3)对模拟图像进行SIFT算法特征检测和匹配。
2.2双分辨率加速
双分辨率加速(Acceleration with Two Resolution )方法[89]是通过对低分辨率目标图像进行2.1节描述的ASIFT算法,该过程首先对输入图像进行低分辨率处理,然后模拟仿射变化,最后对得到的模拟图像应用SIFT算法。
双分辨率方法总结如下:
(1)由一个K×K 采样因子对查询图像μ和搜索图像υ进行二次采样:μ′=SKGKμ和υ′=SKGKυ,其中SK是二次采样抽样算子,GK是一个抗混叠高斯离散滤波器;
(2)低分辨率下ASIFT算法:对查询图像μ和搜索图像υ应用2.1节中所述的ASIFT算法;
(3)确定模拟图μ′和υ′之间最多匹配对的M种仿射变换;
(4)高分辨率ASIFT算法:对原始图像μ和υ使用ASIFT算法,而只模拟确定的M种仿射变换。
2.3ASIFT的复杂度
评估ASIFT的复杂度归结为由低分辨率下ASIFT方法模拟图像区域[10]。图像局部特征的计算量与输入图像面积成正比,ASIFT模拟的全部图像区域也正比于倾斜t:(180/72)t=2.5t,取a=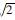 ,n=6,可得:|Γt|=|{1,
,n=6,可得:|Γt|=|{1, ,2,2
,2,2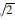 ,4,4
,4,4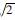 }|=6,模拟图像区域可达到6×2.5=15倍输入图像;通过采用K×K=3×3二次采样,则低分辨率ASIFT算法的模拟图像区域是:
}|=6,模拟图像区域可达到6×2.5=15倍输入图像;通过采用K×K=3×3二次采样,则低分辨率ASIFT算法的模拟图像区域是:![C5J]RCR3$5EEL9G1)2ZUT6U.png C5J]RCR3$5EEL9G1)2ZUT6U.png](http://files.chinaaet.com/images/2016/09/01/6360833694396900009164318.png)
![FFK1SNB_05CC_UUW]EAGKX7.png FFK1SNB_05CC_UUW]EAGKX7.png](http://files.chinaaet.com/images/2016/09/01/6360833694899400001445497.png) 倍输入图像,因此模拟图像会产生原图1.5倍的特征点,复杂度就是SIFT的1.52=2.25倍。这种二次采样的方法大大降低了ASIFT算法的复杂性,把此方法应用到输入的两个匹配图像上,整体的复杂度就只相当于SIFT算法的2倍了。
倍输入图像,因此模拟图像会产生原图1.5倍的特征点,复杂度就是SIFT的1.52=2.25倍。这种二次采样的方法大大降低了ASIFT算法的复杂性,把此方法应用到输入的两个匹配图像上,整体的复杂度就只相当于SIFT算法的2倍了。
3ASIFT算法实验分析
实验在Intel i5 CUP,2 GB内存MATLAB仿真平台上完成,通过仿真对ASIFT算法与SIFT算法匹配效果进行对比,采用匹配对数目作为比较标准,实验图形分辨率为500×670。
(1)绝对倾斜实验:对绝对倾斜进行测试,改变相机光轴与正面视图的角度,分别取纬度θ=30°、75°进行实验仿真,可分别得如图4(a)、(b)匹配图。
(2)过渡倾斜实验:对过渡倾斜τ进行测试,取t=4,分别取经度角φ=30°、80°进行实验仿真,分别得到如图5所示的匹配图(a)、(b)。

实验表明ASIFT算法扩展了SIFT算法的装置,通过仿射模型提出的经度和纬度两个重要参数,模拟光轴变化,充分考虑了实际目标发生的变化,相对于SIFT算法能够检测出更多的匹配对。实验对比图所示SIFT算法的过渡倾斜只能模拟到2,而ASIFT算法可取到16(理论上可达36),有效地量化了两幅图像因角度变化引起的形变。可以看出ASIFT算法不仅继承了SIFT算法完全尺度不变的特性,而且实现了完全仿射不变,保证了特征匹配的准确性、完备性。
4结论
本文对ASIFT算法的研究分析可以看出,ASIFT改进了目前几种先进的特征匹配算法的不足,鲁棒性、稳定性和适应性最好,在实际的目标识别、跟踪等很多方面都有很强的适用性。针对模拟图像引起复杂度增加的问题,提出的双分辨率法有效地降低了ASIFT的复杂度,提高了算法的性能。下一步工作是将该算法运用到实际中,结合实际的需求进一步改善ASIFT算法的性能。
参考文献
[1] 张波,王天召,李科,等.一种改进的Harris特征点匹配算法[J].计算机系统应用,2013,22(7):100103.
[2] MIKOLAJCZYK K, SCHMID.An affine inva giant interest point detector[C].The Seventh European Conference on Computer Vision ,Springerverlag,London,2002,12814.
[3] MIKOLAJCZYK K,SCHMID C.Scale and affine invariant interest point detectors[J].International Journal of Computer.Vision, 2004(60) :6386.
[4] MATAS J,CHUM O,URBAN M,et al.Robust widebaseline stereo from maximally stable extremal regions[J].Image and Vision Computing ,2004,22(10):761767.

