李宇成,刘昆

　　（北方工业大学 电气与控制工程学院， 北京 100144）

       摘要：基于PCA 和SVM提出了一种新的人脸分割法，将双眼、额头、鼻子、嘴等可以明显表征人脸的六类特征提取出来，舍弃双颊以及耳朵等特征量少的部位。融合上述人脸的特征识别结果，运用支持向量机的方法进行分类识别，实验结果表明，文章所提出的PCA与SVM融合的新的人脸分割方法能有效地对人脸进行分类，极大地提升识别率。

　　关键词：人脸分割；人脸识别；主成分分析；支持向量机

0引言

　　如今生物学、机器学习等研究领域中都涉及到人脸识别，将人脸的生理特征与计算机相结合在人机交互场合有着重要的意义。

　　对人脸高效的识别分类关键在于能否提取到精准表征人脸的特征，特征的提取是指通过已有特征的组合（变换）建立一个新的特征子集。在众多的组合方法当中线性变换因其计算简单且便于分析的特点得到广泛应用，主成分分析(Principle Component Analysis, PCA)是其中常用的方法［1］ 。

　　但是在特征提取过程中样本图片维数往往很高，难以对人脸图片特征进行高效的提取，比如图像矩阵为112×92，那么协方差矩阵就是10 304× 10 304，这会导致程序运行时间过长。本文针对这个问题提出了一种新的图像矩阵分割方法，即将双耳以及脸部剔除，最终人脸图像分割成六部分，依次是额头、左眼、右眼、鼻子、嘴、下巴，这六部分包含的人脸特征最为明显，区别度最大。

　　以ORL 人脸库为例：分割后的有效数据量只占原始人脸样本数据的60%左右。但是这六部分矩阵组成的6 400个数据包含了很明显的特征。因为目标矩阵相对较小，所以整个识别过程的完成速度也比传统PCA+SVM方法要快。

1相关算法

　　1.1PCA主成分分析

　　从人脸图像中找出最能表征人脸的特征空间是主成分分析在人脸特征提取中的基本思想，这个过程中不能表征人脸的属性会被剔除。也就是在一个高维特征空间中，利用一组系数对特征加权，来重新表示一张人脸图片［3］，这个过程的数学描述如下：

　　如果训练集中有H张人脸样本图片，将人脸图片训练样本写成一个列向量［xH1,xH2,…,xHK］，下标K是人脸图像的Pixel个数。首先需要获得训练样本中图像的均值，公式 ψ=1H∑Hi=1π(xi)可以求得这个均值，然后通过Ω1=ai-ψ计算出某一样本图像与全部样本均值的差，则人脸训练样本集特征的协方差矩阵为：

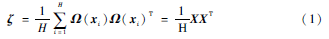
　　式（1）中的矩阵X=［Ω1，Ω2，…，ΩH］，将ζ进行对角化运算，可以将其转化成代数特征空间。将式(1)矩阵ζ对角投影变换为：

　　ζψk=λkψk(k=1,2,…,H)(2)

　　下一步需要选择基向量，基向量应该从ψk中选择最大值。获得U′是包含较大特征值的H′个特征向量。完成上述计算过程后，需要将特征脸映射到它所对应的特征子空间，通过式（3）实现：

　　ρi=U′(xi-ψ)(i=1,2,…,H)(3)

　　计算后可发现ζ的维数很大，如果直接用其进行特征值分解计算，计算的复杂度会非常高，因此这里巧妙地采用了空间的投影求得最终结果［4］。

　　1.2SVM人脸分类

　　SVM(支持向量机) 在解决小样本分类上有很出色的表现［2］。

　　在输入空间X中，令向量X为样本特征集合，其中人脸样本的有效特征xi拥有p类属性。假设任意人脸样本特征xi，则设yi是对应分类输出，yi标记为1时说明是计算后相似的人脸特征；yi标记为－1时则表示不同的人脸样本特征。

　　进一步经以下运算获得人脸特征最优分界面，也就是对凸二次优化问题的求解:

　　min(θ)=θ22，其约束条件为:

　　yi(θ·xi)+b-1≥0，i=1,…，n(4)

　　令mi为拉氏乘子，便可以求出分类判别函数:

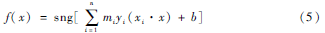
　　由式（4）、（5）可以求解出特征脸中的支持向量，该支持向量是与分界面平行的，而且与分界面的距离最短，支持向量可以唯一确定最优分界面。

2基于人脸分割的PCA和SVM人脸识别方法

　　2.1人脸分割方法

　　人脸分割算法的基本思路是从尺寸为m×n的矩阵I中分别取出FH(额头)、RE(右眼)、LE(左眼)、NS(鼻子)、MU(嘴巴)、JW(下巴)共计6个特征图像矩阵。以嘴部（MU）的矩阵为例来阐述一下这种新分割方法的数学依据以及特征提取方式［5］。如果样本集人脸的图片有H张，Ii(i=1，2，…，H)为全部样本图片，图片尺寸为m×n，将MU变换为D=m1×n1维的列向量XMU。则全体的嘴巴样本训练矩阵为AMU=［XMU1，XMU2，…，XMUM］，嘴巴的协方差矩阵为:

　　式中，UMU是H张嘴巴图片的期望向量。同理，可以得到SRE、SLE、SNS、SFH。对SMU求特征值和特征向量，先假设式中的λi是∑Hk=1(XMUk-UMU)(XMUk-UMU)T的r个不为零的特征值，那么vi就是它关于λi的一个特征向量，则矩阵的正交归一特征向量μi为:

　　然后根据特征值所占的比重选择最大的前p个特征向量:

　　取α=90%。同样可以求解额头、右眼、左眼、鼻子、下巴这几个特征对应的矩阵的特征值和特征向量。

　　2.2对分割后的特征使用PCA方法

　　定义最优投影向量组P1，P2，…，Pd可取为SMU的d个最大特征值所对应的标准正交特征向量。令PMU =［P1，P2，…，Pd］，PMU称为最优投影矩阵。对已知的嘴巴图像样本XMU，将XMU投影到矩阵PMU构成的子空间上，即:

　　Yk=XTMU·Pk，k=1，2，…，d(6)

　　投影特征向量YMU称为嘴巴图片样本矩阵XMU的主成分。

　　按照同样的思路可以解出额头、右眼、左眼、鼻子、下巴这几个部位对应的主成分特征矩阵。

　　2.3将PCA降维特征通过SVM进行分类

　　设YFH、YRE、YLE、YNS、YMU、YJW为PCA抽取的第i个人脸的额头、右眼、左眼、鼻子、嘴巴、下巴6个部分的特征向量，现在需要一个新的联合特征向量i，这个特征向量由上面六个部分的特征向量融合得到，然后识别过程在(M+N)维的SVM特征空间里进行。图1给出了算法整体实现的流程图。

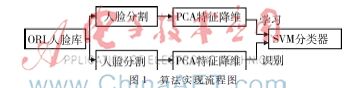
　　3实验过程及结果分析

　　本实验所涉及的人脸图片均来源于包含了40个人，即400 张320×280人脸图像的ORL人脸数据库，图2代表了某一个人的正脸以及他面部六部分分割后归一化的图片数据。

　　根据额、右眼、左眼、鼻子、嘴巴、下巴这几部分，分别将六部分尺寸各异的模块图像矩阵与之一一对应。如图2所示，首先，将这6个模块的特征矩阵用主成分分析(PCA)法提取出来，然后，将提取出的特征矩阵用支持向量机(SVM)方法进行分类。用MATLAB实现的算法识别效果界面如图3所示。

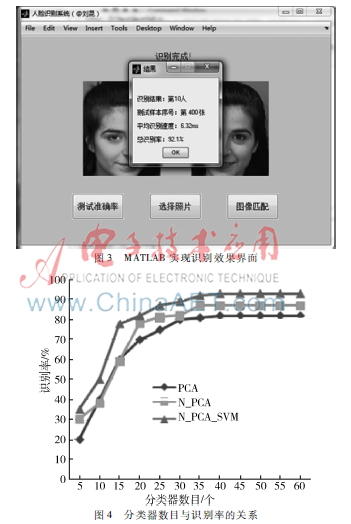
　　将各种算法的识别率性能进行比较，如图4所示，分别代表了以下3种分类器的识别率情况：将PCA 用作特征抽取的人脸分类器、基于新分割PCA (N_PCA)的分类器和在新分割PCA 的方法中引入了SVM分类器(N_PCA_SVM)。由图4可以看出，无论是对于PCA 还是对于PCA+SVM方法来说，在加入新的人脸分割方法进行处理后，其识别率有了显著的提高。

　　在ORL人脸数据库的基础上，进行一次与识别效率有关的测试。因为每张人脸图片基于人脸分割的方法，因此只用了约60%的数据，该实验测试各种方法的运行效率，3种人脸识别算法都执行6次并计算平均执行时间。实验结果如表1所示。

　　实验结果表明：使用新的人脸分割方法处理过的算法程序运行总时间差别较小，而且不会因为分类函数的不同而影响最终效率。新人脸分割的方法仅使用了大约60%的人脸数据，并且还被分成了六个部分，所以用的矩阵一般较小，处理速度也快。

4结束语

　　基于新分割的主成分分析和支持向量机分类器(N_PCA_SVM)，与其他分类器相比有以下优越性：能较好地解决视频人脸跟踪识别过程中高速特征提取问题。因此对实时性要求较高的分类场景具有很大的优势。

　　本文提出基于新分割PCA+SVM(N_PCA_SVM)方法，通过实验证明该方法实时识别速度快，并且识别率高，能用于实时视频监控人脸识别系统。

参考文献

　　［1］ Zhu Yulian． Fuzzy withinclass matrix principal component analysis and its application to face recogntion［J］． Transactions of Nanjing University of Aeronautics ＆ Astronautics，2008，25(2):141147.

　　［2］ 曾阳艳，叶柏龙． 基于支持向量机的人脸识别系统的研究［J］． 计算机工程与应用，2008，44(15):182184.

　　［3］ 王心醉,李岩，郭立红，等．基于双向 PCA 和 K 近邻的人脸识别算法［J］.解放军理工大学学报（自然科学版）， 2010， 11(6):623 627.

　　［4］ 梁淑芬，张志伟，唐红梅，等． 一种应用于人脸识别的非线性降维方法［J］． 电路与系统学报，2009， 14(4):4549．