0 引言

    随着列车运行里程的增加，弹性部件的机械磨损会加剧，使得其刚度系数降低，导致部件性能的蜕化，从而严重影响列车的舒适性和安全性^[1]。传统的列车故障状态分析方法主要针对弹性部件完全故障时对其进行诊断，即只将弹性部件的工作状态分为正常和失效两种。文献[2]通过对列车关键部件的故障信号进行聚合经验模态分解，得到各种工况下的本征模态函数同时提取熵值作为该种工况的特征并进行分类识别。然而实际运行中，列车弹性部件出现完全损坏情况较少，而是随着列车运行里程的增加，部件性能产生蜕化。为了保证列车的安全运行，当弹性部件的参数蜕化达到一定程度时，必须对该部件进行更换。因此，只将列车弹性部件的状态分为正常和失效两种没有太大实际意义，更多的需求是对其参数蜕化程度进行估计^[3]，从而计算出该部件的安全运行裕量，并作为更换和维修部件的依据。抗蛇行减振器作为高速列车的关键部件，为列车提供稳定的回转阻尼力，具有同时满足有效抑制蛇形失稳和利于通过曲线的要求^[4]，对于保障列车的安全性和舒适性有重要作用，本文选取列车抗蛇行减振器进行参数蜕化程度估计具有实际意义。

    Copula函数作为一种分析随机变量间相关性的方法，在近年的研究中得到了广泛应用。文献[5]使用Copula函数分析纹理图像经过小波变换后所得分量间的关联性，并进行特征提取和识别，得到较好的识别效果。文献[6]使用混合Copula函数刻画风电功率间的相关结构并提取特征，对于包含风电场的电力系统风险分析和调度运行有重要意义。文献[7]使用Gaussian Copula函数对高速列车转向架关键器件进行故障特征提取并进行识别，取得了较好的识别效果。

    本文通过Copula函数研究弹性部件在参数蜕化过程中车体转向架的振动信号与车辆正常时信号之间的关联性，得到参数过蜕化程中的演变规律，并对目标信号的参数蜕化率进行估计，对列车的安全运行具有实际指导意义。

1 Copula函数

    Copula函数又名连接函数，通过构建多个随机变量的联合分布函数，反映他们之间的相关性。

1.1 Sklar定理

1.2 常用Copula函数介绍

    Copula函数的常见类型有：椭圆型(Gaussian Copula和t-Copula)、Archimedean型。

    二维Gaussian Copula分布函数定义如下：

    Gaussian Copula函数被广泛应用于联合分布模型的构建，并取得了较好的效果^[9]。

2 Copula函数的参数蜕化率估计

2.1 Copula函数的边缘分布函数构建

    由文献[7]可知，传统的高斯分布模型不能对列车信号的分布进行较好的拟合。文献[7]使用泛化高斯模型(Generalized Gaussian Distribution，GGD)对高速列车信号进行拟合时，得到了较好的拟合效果。验验证结果表明，GGD能对高速列车信号分布进行很好的拟合。故本文采用GGD拟合列车信号的分布，GGD的密度函数的形式为：

    GGD参数计算有最大似然估计和牛顿-拉夫逊法两种，本文使用最大似然估计法计算GGD参数。

2.2 Copula函数构建联合分布及特征提取

    得到信号的边缘分布后，本文采用Gaussian Copula构建信号间的联合分布。

    对Copula函数的参数进行估计时有完全最大似然估计法以及两阶段最大似然估计法两种常用方法。第一种方法通过对边缘分布和Copula函数的参数进行一次性估计，得到全部参数；第二种方法则先估计出边缘分布的参数，然后再求出Copula函数的参数。由于本文已经对信号的边缘分布进行了拟合，故本文采用两阶段最大似然估计法：先求得式(3)中的边缘分布参数，再求出Gaussian Copula函数的参数。

2.3 参数蜕化率估计

    在实际参数蜕化率的估计中，分析特征值随蜕化率的演变规律，根据规律对目标信号的蜕化率进行估计。计算目标信号的特征值，确定与其最接近的值，该值对应的蜕化率作为目标信号的蜕化率。

    本文蜕化率估计方法的流程图如图1所示。

3 实验结果及分析

3.1 数据来源

    采用动力学仿真分析的多刚体动力学分析软件包，针对某型号动车组动车转向架的抗蛇行减振器阻尼在不同参数蜕化率下进行了仿真实验。根据文献[10]，分别设置抗蛇行减振器阻尼刚度系数为正常刚度系数值的90%～10%，以10%进行递减，代表列车弹性部件磨损的加剧，用该百分比代表蜕化率。仿真得到车体后部横向加速度通道、车体中部横向加速度通道、车体前部横向加速度通道在抗蛇行减振器参数蜕化率在90%～10%时的信号。速度设定为200 km/h，仿真时间为3.6 min，采样频率为243 Hz。

3.2 实验结果及分析

    （1）小波包阈值降噪

    数据采集系统的传感器在测量过程中会引入随机噪声的干扰。小波分析具有良好的时频局部特性，通过小波包变换将原始信号分解成不同频域下的成分，进而实现信号滤波以及强噪声背景下对微弱信号特征的提取。高速列车转向架故障振动信号集中在15 Hz以下，选用db2进行4层小波包分解，采用自适应阈值法对样本信号进行消噪预处理。

    （2）GGD拟合边缘分布

    当参数蜕化率分别为90%～10%时，使用GGD分别对车体前部横向加速度通道信号进行拟合，车辆正常时车体前部横向加速度通道信号的分布图以及使用GGD拟合的结果如图2所示。

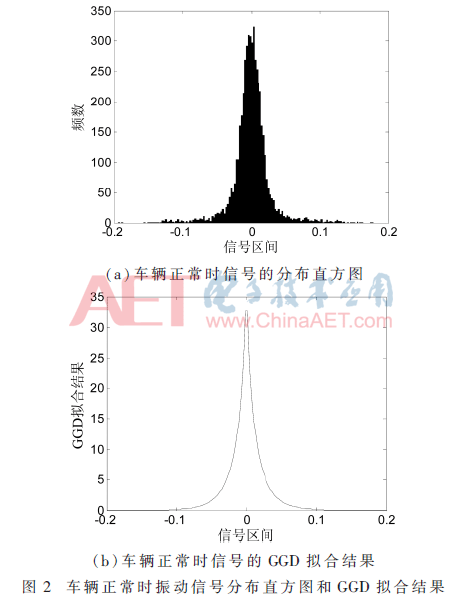
    由图2可知，使用GGD对信号边缘分布进行拟合时，拟合效果较好。

    （3）Copula函数构建联合分布

    使用Gaussian Copula函数分别计算得到9种蜕化信号与车辆正常时信号的联合概率密度函数。提取联合概率密度函数的均值作为特征进行分析，得到不同蜕化率下的信号与车辆正常信号的联合概率密度函数均值的箱形图如图3所示。

    由图3可知，在不同的蜕化率下，列车信号与车辆正常时信号的联合概率密度函数的均值分布区间不同，随着蜕化率的改变呈现出规律性的变化。

    对60个样本的特征取均值，使用3次样条插值法拟合该曲线并对车辆正常时的特征值进行估计，得到联合概率密度函数的均值随蜕化率的变化曲线如图4所示。

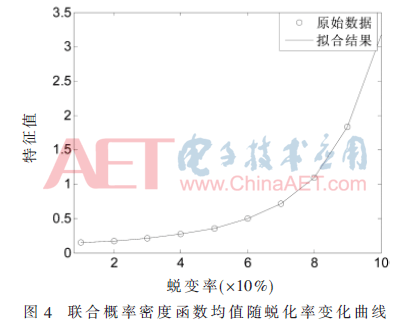
    对应蜕化率从90%～10%，只能得到9个原始数据点，最后一个坐标点的值只能通过估计得到。3次样条插值因具有良好的平滑性和数学特征而得到广泛应用[11]，本文采用3次样条插值法对曲线进行拟合并对最后一点的值进行估计。由图4可知，使用3次样条插值法进行拟合效果较好。

3.3 蜕化率估计结果

    在实际应用中，当参数蜕化率低于60%时，很难保证该弹性部件安全可靠地工作，因此，对蜕化率低于60%的信号进行蜕化率估计无实际意义^[4]，故本文选取参数蜕化率在90%～60%下的信号进行蜕化率估计。

    使用Gaussian Copula函数构建蜕化率待估计信号与车辆正常信号间的联合分布函数，提取联合概率密度函数均值作为特征，使用与其最接近的特征值对应的蜕化率作为估计的结果。为减小样本差异造成的影响，取5次实验得到的特征均值进行参数蜕化率估计，得到车体前部、中部以及车体后部横向加速度通道的估计结果如表1所示。

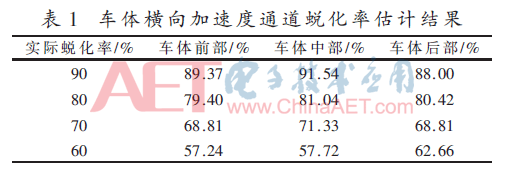
    由表1可知，对弹性部件在实际蜕化率为90%～60%的信号，使用本文所提的参数蜕化率估计方法，在车体前部、中部、后部3个横向加速度通道上的蜕化率估计结果与实际蜕化率之间的误差均在范围内，说明了所提方法的有效性。

4 结束语

    针对高速列车在运行过程中机械磨损导致的转向架抗蛇行减振器参数蜕化，提出了一种基于Copula函数的抗蛇行减振器参数蜕化率估计方法。弥补了传统分析中只将弹性部件分为正常和失效两种工作状态的不足。通过对不同参数蜕化率下的信号进行小波包滤波，并使用GGD拟合信号的边缘分布，最后通过Gaussian Copula函数构建参数蜕化信号与车辆正常信号的联合分布，提取联合概率密度函数均值分析演变规律并进行参数蜕化率估计。对车体前部、中部、后部横向加速度通道信号的实验结果表明，实验误差均在范围内，说明了本文所提方法对高速列车转向架抗蛇行减振器参数蜕化分析的有效性。

参考文献

[1] 王新锐，丁勇，李国顺．铁路火车可靠性实验方法及评价标准的研究[J]．中国铁道科学，2010，31（1）：116-122．

[2] 秦娜，金炜东，黄进，等．基于EEMD样本熵的高速列车转向架故障特征提取[J]．西南交通大学学报，2014，49(1)：27-32．

[3] 丁健明．车辆动力学性能参数估计方法研究[D]．成都：西南交通大学，2011．

[4] 王文静，金新灿，韩同样．动车组转向架[M]．北京：北京交通大学出版社，2012．

[5] Li Chaorong，Li Jianping，Fu Bo．Magnitude-phase of quaternion wavelet transform for texture representation using multilevel copula[J]．IEEE Signal Processing Letters，2013，20（8）：799-802．

[6] 季峰，蔡兴国，王俊．基于混合Copula函数的风电功率相关性分析[J]．电力系统自动化，2014，38（2）：1-5．

[7] 金炜东，吕乾勇，孙永奎．基于Copula函数的高速列车转向架故障特征提取[J]．西南交通大学学报，2015，50(4)：676-682．

[8] NELSON R B．An introduction to Copulas[M]．New York：Springer，2006．

[9] LASMAR N E，BERTHOUMIEU Y．Gaussian copula multivariate modeling for texture image retrieval using wavelet transforms[J]．IEEE Transactions on Image Processing，2014，23(5)：2246-2261．

[10] 张卫华．机车车辆行动动态模拟研究[M]．成都：西南交通大学出版社，2006．

[11] 陈文略，王子羊．三次样条插值在工程拟合中的应用[J]．华中师范大学学报，2004，38（4）：418-422．