马超红，翁小清
　　（河北经贸大学 信息技术学院，河北 石家庄 050061）

       摘要：在总结了近年来关于时间序列早期分类相关文献和相关研究进展的基础上，对参考文献中的学术观点、分类方法进行了比较归类，内容涵盖了时间序列原始数据的早期分类，时间序列早期分类的特征提取与选择、评估方法，早期分类构造模型等方面，为研究者了解最新的时间序列早期分类研究动态、新技术、发展趋势提供了参考。
　　关键词：时间序列；早期分类；特征提取与选择　　

0引言
　　时间序列在狭义上是指按时间顺序有次序的一组数据，而广义上任何实值型的有次序的序列都可以当作时间序列来处理。时间序列分类被广泛应用在医学诊断、灾害预测、入侵检测、过程控制、道路交通等生活中的方方面面。而在很多领域中越早做出分类对于指导决策越有利，时间序列的早期分类应运而生，并在一些时间敏感的应用领域至关重要，例如健康信息学、灾害预测、入侵检测、股市行情预测等领域。
　　时间序列早期分类即针对时间序列数据尽早地做出预测，并满足预期的预测质量(准确率)。换句话说，在满足一个给定的最小的准确率情况下，早期分类尝试着优化分类的早期性，而不是像其他一般分类方法那样只追求最大化准确率［1］。
　　时间序列的早期分类方法大致分为三类：基于原始数据、基于特征和基于模型的分类方法。
1基于原始数据的时间序列早期分类
　　时间序列的早期分类是近几年逐渐开始研究的，Xing Zhengzheng等人［2］在2008年对序列数据的早期预测进行了研究，提出了SCR(Sequential Classification Rule)方法和GSDT(Generalized Sequential Decision Tree)方法。SCR挖掘序列分类规则构造分类器，并根据早期预测效应值在序列枚举树中进行剪枝来选择特征并构造规则。GSDT采用分治策略构造分类模型，在序列特征集中选择分类属性，确保训练集中的每条序列数据至少包含一条所选的属性。SCR和GSDT适用于符号序列(Categorical Sequence)，而时间序列是连续数据，所以在应用于时间序列早期识别时需要对时间序列进行离散化。
　　Xing Zhengzheng等人［34］在2009提出将1NN分类器用于时间序列的早期分类，提出了最小预测长度(Minimum Prediction Length, MPL)的概念和一种时间序列早期分类方法（Early Classification on Time Series，ECTS)，ECTS方法在1NN方法有效的情况下既能保证分类准确率，又能实现早期分类。Xing Zhengzheng等人还提出了Fixed 1NN分类器，即选用固定长度的MPL，适用于2class问题，同时也改进了ECTS，提出了Relaxed ECTS，通过relaxed MPL来避免在原ECTS方法下由于处于决策边界而没有被分类的时间序列，从而提高了分类器的整体稳定性。
　　1NN早期分类器已经取得了较好的研究进展，在实现早期分类的同时其准确度可以与全长序列1NN分类器相媲美。但在一些领域如医学、股市等，早期分类的可解释性十分重要，有助于用户更加信任早期分类的结果，并做出相应的决策。
2基于特征的时间序列早期分类
　　基于可解释性特征的早期分类，目前的方法大都是分为三个阶段，即特征提取、特征选择，最后再将特征用于分类。早期分类中提取的具有可解释性的特征称为shapelet［1］，通俗地讲是时间序列的子序列，某种意义上最大程度地代表某一类的特性, shapelet f=(s,δ,c)其中s表示时间序列，f是s的某一子序列，δ表示距离阈值，c表示s所属的类标号。即如果某一时间序列s′与f的距离小于δ，则判定s′的类别标号为c。
　　Xing Zhengzheng等人［1］在2011年提出在早期分类中提取具有可解释性的特征(Local Shapelets)。针对单变量时间序列，提出了Best match distance(BMD)和BMDlists的概念，并分别使用核密度估计方法(Kernel Density Estimation)和切比雪夫不等式(Chebyshev′s Ineqaulity)来学习local shapelet f=(s, δ, c)中的距离阈值。在选择用于分类的local shapelets时，通过计算每一个shapelets的效用值Utility来进行排序选择，计算方法如下：

　　　提取local shapelet的计算量非常大，对于大数据集则计算时间更长。尽管参考文献［1］中也提出了加速的技术，计算BMD-lists时，在不同的local shapelets中间共享计算结果，但降低其计算复杂度仍然是一个有待研究的问题。提取local shapelets 的方法可用于1NN分类方法无效的情况下。
　　在多变量时间序列早期分类方面，GHALWASH M F等［5］在2012年提出了一种多变量Shapelets检测(Multivariate Shapelets Detection, MSD)方法。该方法采用多变量信息增益选取δ值，在特征选择阶段运用加权信息增益来计算shapelets的效应值，计算公式如下：

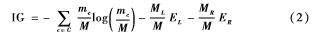
　　He Guoliang等人［67］在2013年针对多变量时间序列早期分类的可解释性，提出了一种挖掘核心特征的方法(Mining Core Feature for Early Classification，MCFEC)，通过实验证明，MCFEC效果比information gain［8］、greedy method［6］等其他方法要好。MCFEC方法用来获得具有区别性且早期的shapelets，并使用提取出的核心特征构造MCFECRules分类器和MCFECQBC分类器。MCFECRules在核心特征中选择可用于早期分类的一致规则来构造基于规则的分类器；MCFECQBC是基于投票选择(query by committee)来进行分类。特征提取阶段采用的是通用方法，将每一个训练样本中满足长度在minL和maxL之间的子序列提取出来组成特征候选集；在特征选择阶段，不同于先前对整体的候选集进行排序的方法。首先采用Silhouette Index将候选集中属于同一变量类标号的特征进行聚类，形成若干簇，基于compactnessseparation 度量将候选shapelets动态地归入最近的簇，另外不同于先前的多变量时间序列早期分类提取的shapelets起点必须相同［5］，MCFEC所提取的各个变量shapelets的起始点和结束点可以不同；运用Fmeasure方法选取距离阈值δ，公式如下：        

　　然后在形成的每一个簇中运用GEFM方法评估特征质量并进行排序，从中选出核心特征，该方法考虑了不平衡性，对于稀有但具有区别性的类核心特征也能选出。GEFM包含对Earliness、Precision、Recall三者的加权。GEFM的计算公式为：

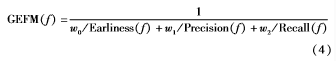
　　同时He Guoliang等人［7］在2013年针对不平衡时间序列的早期预测也进行了相应研究，提出了EPIMTS(Early Prediction on Imbalanced Multivariate Time Series)方法。在构造训练集时采用欠抽样方法来处理不平衡数据集。
　　目前大部分方法是针对数值属性进行研究，LIN Y F等人［9］在2015年针对数值和符号属性(Numerical and Categorical Attributes)的多变量时间序列进行了研究，提出了REACT方法。该方法使用shapelets生成器挖掘等价类(Equivalence Classes Mining)，从多变量时间序列中成功地提取了符号序列的特征，并且考虑了数据集的不平衡问题，采用基于类别比例的子集聚类,评估方案采用平均fscore，如下：

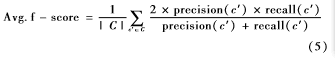
3早期分类器评估方案及现有方法总结
　　时间序列x={(t1,x1),(t2,x2),…,(tL,xL)}的长度为L，且每一个实值{xj∈［1,L］}对应一个时间点{tj∈［1,L］}，训练集中的数据为{(xi,ci)|i∈［1,N］}，其中xi为一条时间序列，ci为其对应的类标号(ci∈C)，C是类标号的有穷集合［10］。早期分类即在完全输入xj前预测其类标号，所以在早期分类中有两个冲突的目标：早期性和可靠性。早期性即尽可能早地对不完全输入序列进行预测；可靠性即分类器输出的准确率问题［11］。DACHRAOUI A等人［11］在2015年提出在多个数据集上对不同的早期分类器采用统计检验的方法(威尔克森符号秩检验Wilcoxon signedrank和帕累托最优Pareto Optimum)进行评估。
　　另外如何对早期分类的两个指标进行权衡，DACHRAOUI A等人［12］在2015年将时间序列早期分类视为非近视的序贯决策树问题，采用通用顺序元算法来实现早期性和可靠性之间的权衡。
　　GHALWASH M F等人［13］在2014年针对可解释性早期分类方法的不确定性估计提供了一种简单有效的方法。没有采用直接估计不确定性的方法，而是将一个时间序列分类c的不确定性定义为：U(c)=1-C(c)，其中C(c)是分类为类c的置信度。同时对EDSC进行了修正，提出了MEDSCU(Modified EDSC with Uncertainty estimates)方法。
　　对于shapelet f=(s, δ, c)中距离阈值δ的计算有以下几种方法：核密度估计函数、切比雪夫不等式、信息增益、Quality(Fβ-measure)。特征提取导致features存在冗余，且不具备代表性，特征候选集数量较大，所以特征选择阶段对候选集进行缩减，主要思路为运用Utility Score 方法对shapelets排序，选取排序第一的shapelet，并将其覆盖的序列在训练集中删除，再选取排序第二的shapelet，重复上述步骤，直到覆盖了训练集中的所有时间序列。目前大致有以下几种指标用于候选shapelet的排序：Utility(f)、GEFM(f)、加权信息增益、Fmeasure(f)。
　　另外,除基于原始数据和特征的分类方法之外，GHALWASH M F等人［14］在2012年针对多变量时间序列的分类构造了早期分类模型(Early Classification Model, ECM),其中集成了隐马尔科夫模型和支持向量机模型。尽管在相同数据集上分类结果的平均准确率较其他方法偏低，但ECM仅用了整个时间序列的40%。
4时间序列早期分类的应用
　　在早期诊断方面，GHALWASH M F等人［12］在2015年提取可解释性的多变量模式(Interpretable Patterns for Early Diagnostics, IPED)来实现时间序列早期分类。首先将时间序列数据转化为二元矩阵(binary matrix)，然后运用凸优化方法在矩阵中提取多变量模式，并采用混合整数离散优化方法来降低时间序列维度，最后将具有可解释性的多变量模式用于临床诊断。
　　在气体识别方面，HATAMI N等人［15］在2013年基于带有拒绝选项的一组连续分类器(Classifiers With a Reject Options, CWRO)，提出了一种时间序列早期分类的模型，并成功应用发明了新型电子鼻——Forefront-Nose。第一个分类器利用一小部分可利用的信号对气体的类型作出决策，第二个分类器利用新的一部分时间序列信号作出决策，分配一个可信的标签或者传递给下一分类器，迭代上述过程直到某个分类器分配了足够可信的标签或者延迟分类的代价太大。
　　DACHRAOUI A等人［16］在2013年将时间序列的早期分类应用于个人电力消费(individual electricity consumption)。实验用的数据集是Irish CER提供的6 000个家庭在500天内，抽样间隔为30分钟的家庭电力消费数据。
5结论
　　时间序列的早期分类在医疗和健康信息学、工业生产管理、安全管理、灾害预测等重要领域都具有广泛的应用，目前已经有了很大的研究进展，但是仍然有很多需要研究的问题。
　　多变量时间序列的早期分类在时间序列挖掘中是一个研究热点，由于它的多变量性和不同组成部分的序列长度可能不同，以及不同变量之间可能存在关联性，很难用传统的数据挖掘算法来对多变量时间序列进行处理，因此将会是一个研究热点［17］。在具体应用中，存储的时间序列以非常快的速度在增长，目前的分类方法大多是基于小型的数据集，所以针对大数据集的早期分类将是一个难点，时间序列每时每刻都在随着时间变化更新，属于流数据［1819］，对于流数据的数据挖掘，如何提高其分类精度同时实现早期分类将会是一个研究热点。另外在基于模型的分类方法研究较少，值得今后进一步研究。
　　参考文献
　　［1］ Xing Zhengzheng, Pei Jian, YU P S, et al. Extracting interpretable features for early classification on time series［C］.SDM, 2011: 247258.
　　［2］ Xing Zhengzheng, Pei Jian, Dong Guozhu, et al. Mining Sequence Classifiers for Early Prediction［C］.SDM, 2008: 644655.
　　［3］ Xing Zhengzheng, Pei Jian, YU P S. Early classification on time series［J］. Knowledge and information systems, 2012, 31(1): 105127.
　　［4］ Xing Zhengzheng, Pei Jian, YU P S. Early prediction on time series: a nearest neighbor approach［C］.IJCAI, 2009: 12971302.
　　［5］ GHALWASH M F, OBRADOVIC Z. Early classification of multivariate temporal observations by extraction of interpretable shapelets［J］. BMC Bioinformatics, 2012, 13(1): 112.
　　［6］ He Guoliang,Duan Yong, Zhou Guofu, et al. Early classification on multivariate time series with core features［C］.Database and Expert Systems Applications. Springer International Publishing, 2014: 410422.
　　［7］ He Guoliang,Duan Yong, Peng Rong, et al. Early prediction on imbalanced multivariate time series［C］.Proceedings of the 22nd ACM International Conference on Conference on Information & Knowledge Management. ACM, 2013: 18891892.
　　［8］ HE G,DUAN Y, PENG R, et al. Early classification on multivariate time series［J］. Neurocomputing, 2014, 149(7): 777787.
　　［9］ LIN Y F, CHEN H H, TSENG V S, et al. Reliable early classification on multivariate time series with numerical and categorical attributes［A］.Advances in Knowledge Discovery and Data Mining. Springer International Publishing, 2015，9077：199211.
　　［10］ 翁小清,沈钧毅. 多变量时间序列的异常识别与分类研究［D］. 西安:西安交通大学，2008.　　

       ［11］ DACHRAOUI A, BONDU A, CORNUJOLS A. Evaluation protocol of early classifiers over multiple data sets［A］.Neural Information Processing［C］. Springer International Publishing, 2014，8835：548555.
　　［12］ DACHRAOUI A, BONDU A, CORNUJOLS A. Early classification of time series as a non myopic sequential decision making problem［A］.Machine Learning and Knowledge Discovery in Databases［C］. Springer International Publishing, 2015: 433447.
　　［13］ GHALWASH M F, RADOSAVLJEVIC V, OBRADOVIC Z. Utilizing temporal patterns for estimating uncertainty in interpretable early decision making［C］.Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining， ACM, 2014: 402411.
　　［14］ GHALWASH M F, RAMLJAK D, OBRADOVIC＇ Z. Early classification of multivariate time series using a hybrid HMM/SVM model［C］.2012 IEEE International Conference on Bioinformatics and Biomedicine (BIBM),  IEEE, 2012: 16.
　　［15］ HATAMI N, CHIRA C. Classifiers with a reject option for early timeseries classification［C］.2013 IEEE Symposium on Computational Intelligence and Ensemble Learning (CIEL),  IEEE, 2013: 916.
　　［16］ DACHRAOUI A, BONDU A, CORNUEJOLS A. Early classification of individual electricity consumptions［C］. Realstream 2013(ECML), 2013, 8190:1821.
　　［17］ HAN J,KAMBER M, PEI J. Data mining: concepts and techniques［M］. Elsevier, 2011.
　　［18］ 原继东, 王志海. 时间序列的表示与分类算法综述［J］. 计算机科学, 2015, 42(3): 17.
　　［19］ 戚陆越, 吴升. 时间序列数据可视化研究综述［J］. 微型机与应用, 2015, 34(12):710.