王蔚
　　（南京邮电大学 自动化学院，江苏 南京 210000）

       摘要：该文主要是利用牵制控制方法对一类具有时延性质的复杂网络进行同步控制。该方法不同于最早的全局控制，仅是对网络中的部分节点进行控制。将这些节点的输出量的差值作为控制器从而达到等同于全局控制的效果。同时根据最新的网络结构可控原理计算出牵制控制所需要的最少节点数目，继而通过设定合适的Lyapunov函数，并基于稳定性和线性矩阵不等式等理论得出满足要求的控制器设计准则。最后，采用小世界模型进行仿真，进一步验证了结论的正确性。
　　关键词：复杂网络；牵制控制；状态延时；最大匹配　　

0引言
　　复杂网络几乎随处可见，如万维网、互联网、无线通讯网络、电力网络等。这些网络都与人们的生活息息相关，对这些网络进行研究不但会促进某些科学分支的发展，还会极大地改变人类的生活方式。因此复杂网络的研究尤为重要。其中，网络同步是复杂网络研究中最重要的一个分支。复杂网络的同步问题可以分为内部同步和外部同步。内部同步是指网络中所有节点最终都收敛于同一个平衡点；外部同步是指不同网络间达到的一种平衡状态［12］。
　　最早关于复杂网络的研究多是基于理想状态下进行的。如今，复杂网络在建模控制及优化时，通常会考虑一些不确定因素，如存在时延。例如，参考文献［3］研究了两类时延复杂动态网络的同步问题，其中一类网络中每个节点的状态具有不同时延，另一类网络中节点不仅状态具有不同时延，每个节点本身的时延也不同。针对这两类网络，利用矩阵测度理论给出了网络同步判据。参考文献［4］考虑在噪声条件下，研究具有不同拓扑结构的时延复杂动态网络的外部同步问题，并采用自适应方法设计控制器。上述这些文献研究的时延复杂网络都是连续型复杂网络，而现实生活中更多的网络是离散型网络，如社会中的人际网络、生物学中的细胞神经网络以及工程应用中的电力网络等。因此研究离散型的复杂网络更具有现实意义。本文主要研究关于离散型时延复杂网络的外部同步控制［56］。
　　最早对网络控制的方法是全局控制，就是对每一个网络节点都施加控制器。但由于实际网络中的节点个数较多，若对每个节点都施加控制会使成本增高，因此通常只是控制部分有利的节点，进而达到对整个网络的控制。这就是目前研究较多的控制方法——牵制控制［7］。牵制控制同样分为内部牵制和外部牵制控制。本文主要利用牵制控制使所研究的复杂网络达到外部同步。
　　参考文献［711］都是对牵制控制的研究，多是基于两个基本问题：一是可行性问题，即仅仅控制少部分节点能否达到网络稳定同步；二是有效性问题，即选取哪些节点来进行控制。参考文献［78］提出了牵制控制的策略，即对网络中的一小部分节点进行线性反馈控制，使网络所有的节点达到同步状态。参考文献［9］利用一个节点来牵制控制整个网络；参考文献［10］利用自适应的方法来牵制整个网络，自适应牵制的方法克服了预估反馈增益的问题。上述这些文献研究的复杂网络基本都是在理想情况下的连续型复杂网络，具有一定的局限性。
　　在分析并结合上述这些文献的基础上，本文构建出一种更为合理的离散型时延复杂网络，并利用Poission过程来描述耦合时延。利用Lyapunov稳定性理论，同时结合随机分析法，给出了离散型复杂网络在存在耦合时延时控制器设计准则。最后，以包含20个节点的离散型复杂网络为例，进行数值仿真，验证本文所提出的控制设计的准确性。
1问题描述
　　假设一个具有时变时延性质的复杂动态网络系统的数学表达式如下：
　　

　　其中,i=1,2,3,...,N,节点i具有n个状态：xi(k)=(xi1(k),xi2(k),...,xin(k))T, f(xi(k))=Aixi(k),Ai∈Rn×n,A=diag(A1,A2,A3,...,AN),Γ∈Rn×n是一个内部耦合矩阵。W=(wij)∈RN×N,表示网络的拓扑结构，其中wij0(i≠j),但不能全部为0。∑Nm=1wkm=∑Nm=1wmk=0(k=1,2,3,...,N)。τ(k)为网络中的时变时滞，假设其满足Poission分布如下：
　　Prob(τ(k)=τ)=λττ!e－τ,τ∈R,0<λ<1，方差σ2=λ。节点i的输出yi(k)∈Rm,C=diag(C1,C2,C3,...,CN)。
2牵制控制器的设计
　　本文采用牵制控制的思想，假设控制的节点属于一个集合S，整个网络的节点属于集合N。
　　

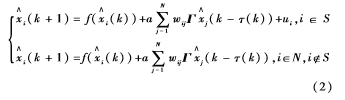
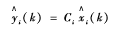
　　用式（2）减去式（1）可以得到误差系统如下：
　　

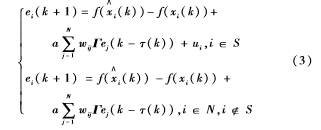
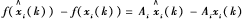
　　设计如下的牵制反馈控制器：
　　

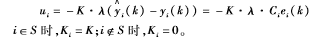
　　在下面论证过程中会用到以下引理。
　　

　　这样状态估计器如（式（2））在牵制控制器ui的选择控制下可以有效地估计复杂网络（如式（1））的状态。
　　证明：构建Lyapunove函数
　　

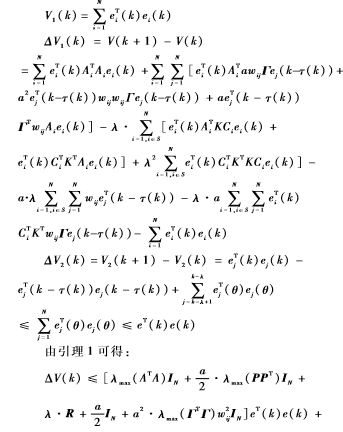
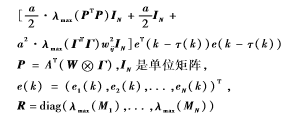
　　W是将W中元素wij替换为a2λmax(ΓTΓ)w2ij后的矩阵。因此，由Lyapunov定理可知：只要ΔV(k)≤0，则当k→∞时，估计误差就将趋于0，继而可以得出状态估计器可以有效地估计原网络的状态信息。从而得出定理1的结论。
3数值仿真
　　仿真中，利用小世界网络模型。该模型是由20个节点组成的复杂网络，同时每个节点有三种状态，可表示为xi=(xi1,xi2,xi3)T,i=1,2,3...,20，参数可设定如下：
　

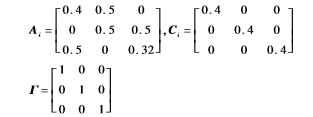
　　根据最大匹配算法可以算出该网络至少要控制3个节点，根据上述判断选取增益矩阵K=(0.9,0.8,0.9)T,其仿真结果如下图1~图3所示，3幅图中横坐标代表时间刻度，竖坐标ei1(k)、ei2(k)、ei3(k)表示节点的估计误差。

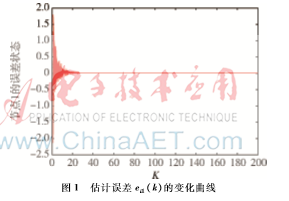
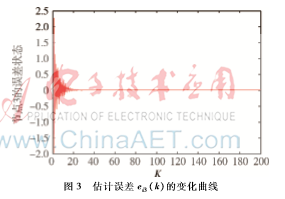
　　由仿真图可知，节点误差收敛于零，故状态估计器（式（2））在牵制反馈控制器ui的作用下可以有效地估计复杂网络（式（1））的状态。
4结论
　　本文主要研究了具有状态延时的离散时间复杂网络的牵制控制状态估计的问题。将牵制控制的方法运用到状态延时离散复杂网络中，即通过控制网络中少部分节点，以达到对整个复杂网络进行状态估计的目的，大大降低了状态估计的成本，具有实际工程运用的价值。利用Lyapunove稳定性理论，给出了牵制控制状态估计器的设计准则，并同时在理论上给出了需要牵制多少个节点才能达到有效进行状态估计的要求。最后，通过仿真实例，验证了所设计状态估计器的可行性和有效性。
　　参考文献
　　［1］ 汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用［M］. 北京：清华大学出版社, 2006.
　　［2］ 陈关荣. 复杂网络及其新近研究进展简介［J］. 力学进展, 2008, 38(6): 653662.
　　［3］ Feng Cunfang. Projective synchronization between two different timedelayed chaotic systems using active control approach［J］.Nonlinear Dyanmics， 2010，62(12):453459.
　　［4］ Wang Guanjun, Cao Jinde, Lu Fanguan. Outer synchronization between two nonidentical networks with circumstance noise［J］.Physica A,2010,389(7):14801488.
　　［5］ Liu Bin,TEO K L,Liu Xinzhi. Global synchronization of dynamical networks with coupling time delays［J］.Physics Letters A,2007,368(12):5363.
　　［6］ 濮志平.具有时延的复杂网络状态估计［D］.南京：南京邮电大学,2015.
　　［7］ 章剑林,王磊,戴华平. 基于线性矩阵不等式的牵制控制策略分析［J］. 上海理工大学学报,2008,30(3):222226.
　　［8］ 樊春霞, 蒋国平. 输出耦合的复杂网络自适应牵制同步［J］.应用科学学报, 2010, 28(2): 203208.
　　［9］ Li Xiang, Wang Xiaofan, Chen Guanrong. Pinning a complex dynamical network to its equilibrium［J］.  Circuits and Systems I Regular Papers IEEE Transactions on, 2004, 51(10): 20742087.

　　［10］ ZHOU J, LU J A, L J. Pinning adaptive synchronization of a general complex dynamical network［J］. Automatica, 2008, 44(4): 9961003.
　　［11］ 赵军产, 陆君安, 吴晓群. 一般复杂动力网络的优化牵制控制［J］.中国科学：信息科学, 2010, 40(6):821830.