孙彦子1，范红1,2，陈静1,马海全1

　　（1.东华大学 信息科学与技术学院，上海 201620;

　　2.东华大学 数字化纺织服装技术教育部工程研究中心，上海 201620）

    摘要：在气象预测过程中，静止气象卫星全天候工作，其拍摄的卫星云图在灾害性的强对流天气监测与预警方面发挥了重大作用。对多波段的红外云图进行分类前的融合、压缩预处理，对提高云图的分辨率，减轻数据传输压力，以及加强夜间探测能力，都具有现实意义。文章对KL变换及小波变换两种预处理方法进行对比。实验结果表明，基于KL变换的预处理方法处理后效果与源图像的差异更小，得到的红外云图也与同时段可见光云图最接近，对红外云图更适用。小波变换则更多地保留了源图像细节信息，适用于预处理后的云图研究。

　　关键词：红外云图；预处理；KL变换；小波变换

0引言

　　气象卫星属于一种专门的对地观测卫星或遥感卫星，主要负责对大气层进行气象观测。气象卫星能够从太空上，借助各种遥感仪器观测并记录地球及其大气层的可见光、红外数据，将云图等气象信息下发给地面站。气象卫星具有范围广、时效快、数据质量高、受限度小等优势，它所提供的气象信息己广泛应用于日常气象业务、气象科学、海洋学和水文学的研究，例如美国”泰罗斯”号气象卫星系列、中国的风云系列卫星均表现出色。

　　静止气象卫星获得的云图主要分为可见光云图和红外云图，前者因借助于地面或云面对太阳光的反射过程拍摄，只限于白天工作；后者通过测量地表物体和大气层的红外辐射程度，全天可获得［1］。与地面站传输通信前，实现对红外波段云图的压缩、融合预处理，对气象监测作用不可小觑。本文从多光谱图像的特性分析着手，提出基于它的两种预处理方法，并对此进行比较，分析各自优势和适用情况。

1多光谱图像特性分析

　　遥感各波段记录了地物波谱的微弱差异，充分利用地物在不同波段的差异，可以更有效地识别物体。红外云图是气象卫星在红外波段通过红外感应器测量来自云顶、地表物体所发射的红外辐射总量并向地面站发送的云图［1］。它具有一般红外图像的特征。

　　红外图像一般较暗，分辨率低，边缘模糊。图像上深色物体灰度值较高，辐射能力强，温度高；浅色物体灰度值较低，辐射较弱，温度低。因此通过红外云图，可以判断云顶的高度，从而预测天气状况。当处于晴天时，卫星观测到的数据是从地表发向太空的红外辐射，红外云图上表现为黑灰色，颜色越深，天气越晴朗；雨天时，卫星观测到的数据是从云顶发向太空的红外辐射，红外云图上表现为灰白色，颜色越白，表明气温越低，云层越厚实，降雨强度越大；阴天时，红外云图上表现为深灰、灰、浅灰色系，表明有不同厚度的云而无明显降水。红外云图可以在完全无光的夜晚或者烟云密布的条件下获得图像，这一点是可见光云图不可媲美的［2］。本文重点分析红外云图，并与同时次的可见光图像进行比对。

2红外云图预处理

　　基于红外云图的特性，对此进行分类前预处理，将来自多个传感器、不同波段的红外云图进行融合压缩，获得比单一图像更加可靠、准确的数据，实现实时传输，为灾害性天气检测和预警准确性提供保证。多光谱图像的各波段之间具有一定的相关性，它们的数值以及显示出来的视觉效果往往相似，造成不同信息的重叠。图像各波段之间的相关可能是以下几个因素结合起来引起的：(1)物质的波谱反射相关性；(2)地形；(3)遥感器波段之间的重叠。从不同波段的红外云图中可以发现一个共性：陆地、海洋等地貌特征相关性较高，云朵的相关性较低，故在此基础上，只需提取出最有用的云朵信息即可，减轻了预处理的工作量。

　　2.1基于KL变换的方法

　　对不同波段的红外云图进行预处理，主要目的是从多幅红外云图中提取出相关性较低的云朵信息。一种方法就是对红外云图进行去相关性的变换。本文选择使用离散的KL变换（又称霍特林变换），它将多波段空间中的图像数据映射到所选取的主成分空间中，将各波段有用信息压缩到尽可能少的主成分中，起到了信息压缩和信息分离的效果，便于各波段信息量的计算。

　　离散的KL变换具有很高的去相关性，是均方误差条件下的最佳变换，在图像的压缩和融合等方面应用广泛。其融合合成速度较快，但由于对图像中的所有像素处理均一致，因此它往往会丢失弱小的重要目标，不适用相关性较弱的图像。由于红外云图都是针对同一时间、同一地点、相同目标获取的图像，相关性较强，因而此方法很适合［3］对红外云图的处理。

　　设从同一个随机母体得到了M个矢量采样，则其均值矢量和协方差矩阵可分别由以下两式利用采样来近似：

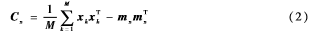
　　因为矩阵Cx是一个实对称矩阵，所以总可以找到它的一组N个正交特征值。现令ei和λi(i=1,2,…,N)分别为Cx的特征矢量和对应的特征值，并且这些特征值单调排列，即λi≥λi+1(i=1,2,…,N-1)。

　　设Cy是一个对角矩阵，它的主对角线上的元素正是Cx的特征值，即：

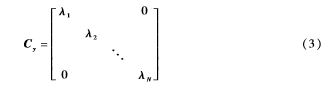
　　则：

　　式(4)就称为KL变换［4］。

　　基于KL变换的红外云图预处理主要包括以下几步：(1)在多幅图像对应像素之间建立矩阵；(2)将原始矩阵进行中心化（将矩阵中每一个元素都减去样本的均值），然后计算其协方差矩阵；(3)计算协方差矩阵的特征值，将特征值按从大到小的顺序排列组成新的特征矢量（特征矢量为对角矩阵，主对角线上的元素为特征值）；(4)对新的特征矢量进行KL变换，取出第一分量，即得到第一主成分图像。

　　2.2基于小波变换的方法

　　近年来，小波变换在图像处理领域中的地位越来越突出，基于小波变换的图像压缩、融合技术则成为国内外研究的热点。小波变换主要包括连续小波变换和离散小波变换,在图像处理中主要使用离散小波变换。将小波变换理论应用到图像融合中，实际上就是对图像进行小波分解，产生基于图像的低频和高频两部分信息，再分别针对这两部分进行融合处理。小波变换后低频系数表征源图像的近似信息，大体反应图像的轮廓；高频系数表征图像的细节信息，如边缘、线条以及区域边界等。红外云图包含的信息比较丰富，但其边缘不够清晰。因此基于小波变换的方法，主要针对高频分量进行处理，以此提高整体图像的分辨率。

　　离散小波变换（DWT）是通过一组低通分解滤波器(g)和高通分解滤波器(h)来对图像进行分解实现的。通过小波变换将原图像按不同频带和分辨率分解成一系列子带图像，每一层小波系数分解成如下4个子带：LL(低频部分，显示为近似图像)、LH(高频部分，显示为垂直高频图像)、HL(高频部分，显示为水平高频图像)、HH(高频部分，相当于45°斜线方向的高频图像)。然后小波分解对每层得到的低频分量LL继续进行下一个尺度的分解，但对高频分量不再做任何分解［5］。

　　以一幅大小为M×M的图像f(x,y)为例，进行j层分解：

　　当j=1时，

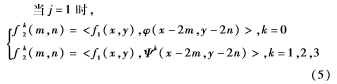
　　当j>1时，

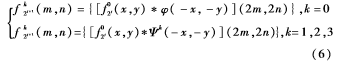
　　其中，φ(x,y)为二维尺度函数；Ψk(x,y)(k=1,2,3)为二维基本小波。

　　若要重构图像，通过另一组低通重构滤波器(g-)和高通重构滤波器(h-)就可以逐级重构出原图像［2］。

　　针对红外云图的特点，基于小波变换方法的预处理基本步骤为：(1)对多幅原始图像进行几何配准，保证图像大小一致；(2)分别对它们进行二维离散小波变换，得到图像的高低频分量；(3)针对低频分量，采用基于像素的融合规则，即采用平均值；(4)针对高频分量，采用基于区域的融合规则，即区域方差法；(5)对融合后的高低频分量经过小波逆变换重构得到融合后的图像。

　　其中区域方差法的基本思想是：对待融合图像在小波变换后的频率域，计算待融合图像的对应空间域的区域方差以及方差匹配度，然后根据方差匹配度与阈值的比较确定融合图像的小波分解系数。若匹配度小于阈值，则取区域方差大的相应点的分解系数作为融合图像的分解系数；若匹配度大于阈值，则采取加权平均方法得出相应的分解系数［6］。

3实验结果与分析

　　本实验中，选取我国风云二号气象卫星3个红外通道的原始数据图像进行预处理，使用MATLAB编程实现，如图1~图3所示。图1是3幅原始图像，图2显示KL变换后的图像，图3显示小波变换后的图像。

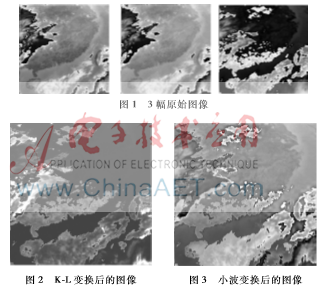
对于图像除了视觉效果评价外，还可以通过一些参数进行客观评价，表1给出了原始图像和两种变换的结果进行数据比较。本文主要通过计算图像的信息熵、平均梯度值、交叉熵、均方根误差4项指标对预处理后的红外图像进行评价。图像的信息熵E是衡量图像信息丰富程度的一个重要指标，其大小体现了图像所包含的平均信息量的多少。图像的熵值越大，表示图像的信息量越大，质量越好；平均梯度值 反映了图像中的微小细节反差表达能力和纹理变化特征，同时也反映了图像的清晰度。越大，表示图像越清晰；交叉熵CE用来测定两幅图像灰度分布的信息差异。多幅源图像和融合后图像间的综合差异用平均交叉熵MCE评估，该值越小，融合后图像与源图像的差异越小，该算法从源图像中提取的信息量就越多，融合效果越好；均方根误差RMSE用来评价融合图像与标准参考图像之间的差异程度［7］。这里选取的是同时段的可见光云图，如图4所示。RMSE值越小，表明融合图像与理想图像越接近，融合质量越好。

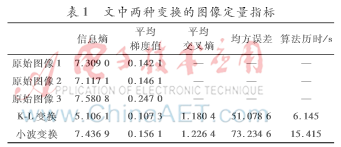
　　从表1结合效果图可以看出, 经过变换后图2、图3两幅图像均去掉了像素点间的相关性，得到不同波段红外云图的互补信息，使得处理后的图像能够含有更丰富的源图像信息。进一步对比可以发现，经过小波变换后图像的信息熵和平均梯度值要高于KL变换，说明小波变换能更好地保留原始图像信息。然而，KL变换后的平均交叉熵和均方根误差比小波变换的小，说明KL变换的效果与源图像的差异更小，得到的红外云图也与同时段可见光云图最接近。从视觉上看，经过KL变换后的图2更好地去除了源图像间相关性高的陆地、海洋等信息，将相关性低的云图信息很好地保留，而且算法历时不足小波变换的一半，真正实现了高效率、高质量的预处理。KL变换更适用于静止气象卫星红外云图的预处理，而小波变换尽可能保留源图像的细节信息，可有效地将来自不同云图的特征与细节融合起来，获得丰富的图像信息，因而更适合于预处理后云图结构细致化分析。

4结论

　　静止气象卫星红外云图在气象预测过程中发挥重要作用，弥补了可见光的不足，为全天监测气象提供了保证。预处理实验对两种变换方法进行验证，实验结果的主观分析和客观评价表明，小波变换将高低频分开处理，能更好地保留源图像的细节信息，对于预处理后的云图结构分析更显优势。 KL变换是在统计特征基础上的多维正交线性变换，应用到多波段、多时相遥感图像应用处理中。采用KL变换的目的是减少各波段信息之间的冗余，达到了保留主要信息、压缩数据量、增强和提取更具有目视解译效果的新波段的目的。随着遥感手段的发展，遥感图像在空间分辨率和波谱分辨率方面都在不断提高，KL变换以及由KL变换引申出的其他变换方法的应用价值也愈显重要。

　　参考文献

　　［1］ 朱青. 卫星红外云图与可见光融合方法研究［D］. 青岛：中国海洋大学，2010.

　　［2］ 李俊山，扬威，张雄美. 红外图像处理、分析与融合(第1版)［M］. 北京：科学出版社，2009.

　　［3］ WITTENBRINK C M, LANGDON J GLEN G, FERNANDEZ G.Feature extraction of clouds from GOES satellite data for integrated model measurement visualization［C］. Proc: SPIE 2666, Image and Video Processing IV, March 13, 1996, 2666: 212 222.

　　［4］ 章毓晋．图像工程（上册）图像处理（第2版）［M］. 北京：清华大学出版社，2006.

　　［5］ 汤仁民，李国芳，王代强. 基于小波的图像基本处理技术研究［J］. 微型机与应用，2015，34（2）：4446.

　　［6］ 李亚春, 武金岗, 王净，等．多小波变换图像融合规则性能的分析研究［J］. 计算机工程与应用，2010，46（8）:180  182，189.

　　［7］ 苗启广，叶传奇，汤磊，等.多传感器图像融合技术及应用（第1版）［M］. 西安：西安电子科技大学出版社, 2014.