黄增先,王进华
(福州大学 电气工程与自动化学院,福建 福州 350108)
摘要:针对G3-PLC物理层信道编码的要求,设计了一种RS译码器。为了解决译码过程中有限域乘法器存在的连线复杂、运算速度慢等问题,设计了一种查表运算。采用该查表运算可以快速实现有限域的乘法运算,并且可以简化BerlekampMassey (BM)迭代过程中的求逆运算,使得用传统的BM迭代就可以高效地实现RS译码。结合FPGA平台,利用Verilog硬件描述语言和Vivado软件对译码器进行设计与实现。时序仿真结果与综合结果表明,该译码器资源占用率低,能够在100 MHz系统时钟下进行有效译码。
关键词:G3-PLC;RS译码器;FPGA;BM迭代
0引言
G3-PLC是由G3-PLC联盟于2009年推出的窄带电力线通信规范,目前已经得到多个国际标准体系的认可,并被几个主要国际电表商采纳。电力线信道条件恶劣,存在多种干扰,使得数据在电力线上传输误码率较大。RS码在纠正随机错误和突发错误方面效果显著,在G3-PLC信道编码系统中,添加RS模块比未加RS模块在10-4 BER(Bit Error Rate)条件下至少多了1 dB的编码增益[1],这充分说明了RS码在G3-PLC系统中的重要性,它能够有效提高系统通信的可靠性。
RS译码过程的运算定义在有限域上,因此有限域运算的设计对译码器的整体性能具有重大的意义。有限域运算的主要难点在于有限域乘法运算和有限域求逆(除法)运算的硬件设计。目前,有限域乘法器的电路实现主要有比特串行结构和比特并行结构[2]。比特串行结构采用时序电路设计,具有占用资源少的优点,但运算速度较慢。比特并行结构采用组合逻辑结构来实现,运算速度快,但连线复杂。根据伽罗华域的性质,可以将有限域求逆运算转化为乘法运算[3],因此可用有限域乘法器实现求逆运算,但还是难以避免有限域乘法器本身所具有的缺点。为避免求逆运算的复杂度过大,人们提出了改进的BM算法,使BM迭代的过程中无需求逆运算[4-5]。无求逆的BM算法可以有效避免求逆运算,但算法的证明复杂。针对上述问题,本文提出了一种查表法来实现有限域乘法与求逆运算,简化了有限求逆运算硬件实现的复杂度,使得用传统的BM迭代就可以高效地实现RS译码。
1基于G3-PLC的RS码结构
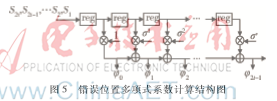
RS码是非二进制BCH码的一个重要子类。RS码的最小距离等于它的奇偶校验符号数加一,是GF(2m)上具有极大最小距离的线性分组码。基于G3-PLC的RS码的生成多项式为:

其中α为伽罗华GF(28)上的本原元素,t=8为可纠正符号数[67]。相应的本原多项式为:
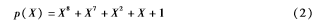
G3-PLC系统中根据不同的通信速率与信道环境,物理层选择不同的符号数和调制方式,因此造成码字长度不同。当调制方式为DQPSK时,总共有6种可选的码字长度,分别为:(251/235)、(233/217)、(179/163)、(143/127)、(89/73)和(53/37),这些码字都是RS(255/239)的缩短码,具有相同的译码结构与纠错能力,因此文中以RS(251/235)为例进行设计与实现。
2RS译码的原理与实现
基于BM迭代的译码算法,由于其实现过程较为简单,译码速度快,是最为常用的RS译码算法。译码的一般步骤为:
(1)计算接收码字R(X)的2t个伴随式Si,i=l,2,…2t;
(2)利用BM迭代算法求出错误位置多项式;
(3)利用钱搜索(Chien Search)求解错误位置多项式的根以确定错误位置;
(4)利用福尼算法求出错误位置上的错误值;
(5)由以上步骤得到错误多项式E(X),则纠错后的码字多项式为:

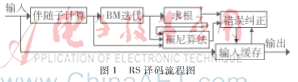
由上述步骤可知,RS译码器必须包含4个模块,即伴随子求解模块、BM迭代模块、求根模块、福尼算法求错误位置系数模块。相应的译码流程如图1所示。
2.1有限域查找表的构造
RS译码算法中的四则运算是在相应的伽罗华域中进行的,传统的有限域乘除运算实现比较复杂,使用查表法可以简化有限域乘法运算与求逆运算。
伽罗华域元素通常有向量表示形式和幂次表示形式,比如GF(28)中元素α1的向量表示形式为(00000010),其中向量表示形式有利于有限域加法运算,而幂次表示形式有利于乘、除法运算。查表运算的过程是通过查表来实现伽罗华元素向量表示形式与幂次表示形式的互相转换,这样就可以根据相应的运算要求来切换伽罗华域元素的表示形式以达到简化运算的目的。构造图2所示两个存储空间,分别用来存储GF(28)域中元素的幂次形式与向量形式。
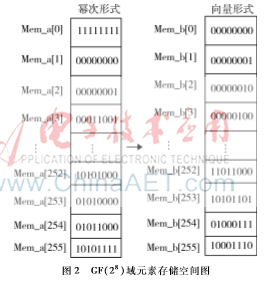
在进行伽罗华元素乘法运算时,首先将向量形式转化为幂次形式,进行幂次相加对应的就是乘法运算,幂次相减对应的就是除法运算,接着判断向量形式中的元素是否有0变量,如果有则向量域地址为0,没有则将幂次域和对255取模加1后的值作为向量域的地址。最后将运算结果重新转化为向量形式。
计算a×b伪代码如下:
y1=Men_a(a);
y2=Men_a(b);
y3=y1+y2;
if(y1==11111111||y2==11111111)
y4=0000000;
else
y4=Men_b(mod(y3,255)+1);
相应计算a÷b即a×b-1的伪代码为:
y1=Men_a(a);
y2=Men_a(b);
y3=y1-y2;
if(y1==11111111||y2==11111111)
y4=0000000;
else
y4=Men_b(mod(y3,255)+1);
2.2伴随子计算
假定接收多项式为:
R(X)=r0+r1X+r2X2+…+rn-1Xn-1
则由
Si=R(αi),1i2t
得:
Si=r0+r1αi+r2α2i+…+rn-1αi(n-1)
直接用该式进行硬件实现时需要相应配置码字的长度,这在实现过程中比较繁琐,因为G3-PLC系统中,采用DQPSK调制时有6种可选的码字长度,这就需要配置6种不同伴随子计算模式。将伴随子的计算式稍作变形可得:
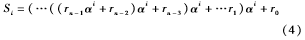
因此伴随子计算的硬件结构可用图3表示。
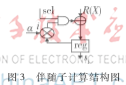
在计算伴随子的过程中只需通过配置αi的值来得到相应的伴随子,从而可以适应不同的码字长度。基于G3-PLC系统的RS码译码器的输入需要进行串并转换,所以每个码元的输入将保持8个时钟周期,在每个码元输入的时钟周期内配置i的值为1,2,3…8,当所有码元输入结束后将得到8个相应的伴随子S1,S2,S3…S8,通过复用一次图3所示结构单元,在每个码元输入的时钟周期内配置i的值为9,10,11…16,可得到S9,S10,S11…S16。
2.3BM迭代
定义错误位置多项式σ(X)为:
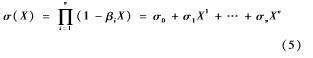
其中βi表示错误位置,BM迭代的具体过程如下:
(1)初始化。令k=1,σ(1)(X)=1,d1=S1,T(1)(X)=X,N1=0。其中N表示此刻对应的错误位置多项式的最高次幂,T表示修正项。
(2)判断修正系数dk是否等于0。如果dk≠0,则σ(k+1)(X)=σ(k)(X)+dkT(k)(X),接着计算T(k+1)(X),首先判断2Nk是否大于等于k,如果2Nk<k,则T(k+1)(X)=d-1kX1σ(k)(X);如果2Nkk,则T(k+1)(X)=X1T(k)(X)。如果dk=0,则σ(k+1)(X)=σ(k)(X),T(k+1)(X)=X1T(k)(X)。
(3)计算下一步的修正系数:
dk+1=Sk+1+∑°σ(k+1)(X)i=1Sk+1-iσi
其中°σ(k+1)(X)表示σ(k+1)(X)的最高次数。更新Nk+1的值,即Nk+1=k-N。
(4)更新k的值,即k=k+1。
(5)判断k是否小于2t。如果k<2t ,则回到步骤(2);如果k=2t,则σ(2t)(X)就是错误位置多项式。
步骤(2)中出现的求逆运算用2.1节中介绍的查表运算来实现,使得用传统的BM迭代就可以高效地实现RS译码。
2.4钱搜索与福尼算法
求解σ(X)的根,由于σ0=1,所以0元素不是σ(X)的根,因此将伽罗华域GF(28)中的所有非零元素一个一个代入错误位置多项式σ(X)中,求得的根取其乘法逆元就可以得到错误位置。最后用图4结构来实现,第一个时钟周期不进行乘法运算,相当于判断σ(α0)是否等于0,从第二个时钟周期开始先进行乘法运算,再求和判断。经过255个时钟周期就可以遍历GF(28)所有非0元素。
由关键方程:
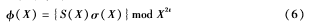
可知(X)的最大次数为2t-1,因此定义:
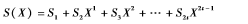
所以有错误值多项式:
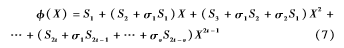
根据图5结构求得错误位置多项式2t个系数后,由福尼算法得错误位置βk上的错误值δk为:

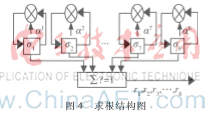
2.5错误纠正
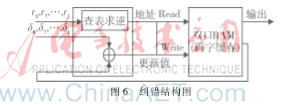
经过上述操作可求得错误位置以及错误位置上的错误值。将σ(X)的根进行查表求逆后可得错误位置,将这个错误位置值作为码字缓存空间的读地址,读出错误码字后与相应的错误值进行异或运算,得到的更新值重新写回原先的地址,使错误码字得到修正。具体结构如图6所示。
3RS译码器的仿真及综合结果
3.1仿真结果
为了便于观测结果,将第一帧待编码字设为[235:1],令编码后的前8个位置为错误位置,使得接收值为[8 7 6 5 4 3 2 1],即将[8(235) 7(234) 6(233) 5(232) 4(231) 3(230) 2(229) 1(228) 227…206 122 61]作为译码器输入的第一帧,其中括号内为正确值。利用Candence公司的NC-Verilog Simulator对设计进行仿真,通过仿真图7、8可以看出,8个错误全部得到纠正。
3.2综合结果
通过Vivado 进行综合与实现,并利用Xilinx xc7k160tfbg4841 FPGA进行硬件实现。实现过程中用到的RAM和ROM由Vivodo中IP Catalog[8]产生。最终,BM迭代模块、纠错模块、求根模块、错误值计算以及伴随子计算模块分别用了517、721、413、572、525个LUT单元。在100 MHz时钟约束下建立时间与保持时间都留有裕量,说明译码器的工作频率至少可以达到100 MHz。


4结束语
本文阐述了基于G3-PLC的RS译码器的译码原理与实现结构。提出一种查表运算来实现有限域的乘除法运算,提高了运算速度并且实现简单。用NCVerilog Simulator对设计的译码器进行仿真验证,给出了仿真时序图,结果表明所设计的RS译码器能纠正8个符号的错误。最后利用Vivado对设计进行综合,并由Xilinx xc7k160tfbg4841 FPGA进行硬件实现。本设计所占的资源较少,不到总资源的3%。
参考文献
[1] RAZAZIAN K, UMARI M, KAMALIZAD A. Error correction mechanism in the new G3PLC specification for powerline communication[C]. Power Line Communications and Its Applications (ISPLC), 2010 IEEE International Symposium on. IEEE, 2010:5055.[2] 聂鹏. OFDM系统中高速RS码的研究与实现[D]. 武汉:华中科技大学, 2012.
[3] 林舒. 差错控制编码[M]. 北京:机械工业出版社, 2007.
[4] DAS A S, DAS S, BHAUMIK J. Design of RS (255, 251) encoder and decoder in FPGA[J]. International Journal of Soft Computing & Engineering, 2013, 2(6):391394.
[5] 石宇, 黑勇, 乔树山. 一种用于PLC系统的多码率
RS码译码器[J]. 微电子学与计算机, 2014(2):5761.
[6] RAZAZIAN K, UMARI M, KAMALIZAD A, et al. G3PLC specification for powerline communication: overview, system simulation and field trial results[C]. IEEE International Symposium on Power Line Communications and ITS Applications, 2010:313318.
[7] Electricite Reseau Distribution France. G3PLC Physical Layer Specification[Z].2009.
[8] 孟宪元. Xilinx新一代FPGA设计套件Vivado应用指南[M]. 北京:清华大学出版社, 2014.

