桑坤,朱向冰,金慧敏
(安徽师范大学 物理与电子信息学院,安徽 芜湖 241000)
摘要:自整角机是一种用于角度测量的微型电机,其输出包含角度的模拟信号经过简单处理和A/D变换后再通过CORDI算法解码。CODIC算法具有精度灵活可调、运算速度快、硬件实现简单等优点;通过对CORDC算法角度及对自整角机输出信号的象限修正,设计了一种基于CORDIC算法流水线技术的自整角机解码算法,并以FPGA为平台进行模拟和仿真,验证其准确性及可行性。
关键词:CORDIC算法;自整角机;解码;FPGA
0引言
自整角机是一种高精度的角度位置传感器[1],广泛应用于航海、航天、方位同步指示系统火炮等伺服系统中。自整角机输出信号主要以模拟信号进行传送,减少角度信号在较长距离传输时其他信号干扰,同时方便人们控制目标元件。传统的轴角测量通常采用峰值采样、相干解调或专用的轴角数字转换芯片实现[2],但是这几种算法也存在精度不高、运算速度较慢及价格昂贵等缺点。本文使用的坐标旋转数字计算(Coordinate Rotation Digital Computer,CORDIC)算法采用迭代的思想,不进行乘法运算,提高了运算速度。由于该算法是一种数字数字的算法,有线性的收敛域和序列及迭代次数可有效提高精度[3]。
本文利用CORDIC算法[4]计算反正切函数并结合自整角机输入输出信号的特点,实现一种运算速度高、可靠性好、精度高、硬件设计简单的角度解码,并用FPGA丰富硬件资源简化程序,提高电路的运算速度和可靠性。
1自整角机基本原理
自整角机是利用自整步特性将转角变为交流电压或由交流电压变为转角的感应式微型电机,当激励绕组以一定的频率交流电压励磁时,输出绕组的电压幅值与转子转角成正余弦函数关系[5]。在结构上,自整角机主要由转子和定子组成,转子轴上的单相绕组通过电刷和滑环与外界连接,引出端用Z1和Z2表示;定子的三相对称绕组以Y型连接,空间位置上依次落后120°,如图1所示。

设转子转动θ,自整角机三路输出模拟信号,但是需要电压激励。激励电压为:

S1、S2、S3三路定子的感应电动势分别为:



上式中sinωt为交流信号,θ是自整角机偏转的角度。
2CORDIC算法原理
CORDIC算法基本思想是迭代,通过多个固定的及与运算有关的角度逐次递减,从而逐渐逼近需要的角度。

CORDIC算法的基本公式在一些文献中有详细推导,这里仅作简要的说明。
如图2所示,假设向量(xi,yi)按照一定角度旋转到(xj,yj)则有:

起始位置到终点位置可以通过多步迭代旋转过程实现,每一步旋转一定的相位,则:
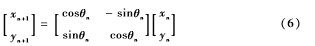
提取cosθn,则有:

定义每一步的旋转角度为θn=arctan(12n),总的旋转相位为θ=∑Snθn,其中Sn=±1,则:

其中K为增益因子,其值的变化取决于迭代次数,当迭代次数N很大时:

CORDIC算法有旋转模式(rotation)和矢量模式(vectoring)两种旋转模式[6],该解码算法采用矢量模式。迭代方程如下:
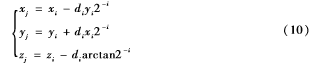
其中zj是角度累加器,di=-sgn(yi)=1,y<0(顺时针旋转)
-1,y>0(逆时针旋转)。
假设初始条件为x0=x,y0=y,z0=0,经过n次迭代后,矢量模式的表达式为:

3自整角机解码算法设计
3.1自整角机输出信号的象限修正
利用CORDIC算法计算反正切值[7],由于arctan2-i(0≤i≤n)所能计算的值区域为-π2,π2,要计算全角度时必须对角度进行预处理。将公式(2)-(4)整理得:
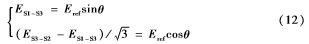
对自整角机三路输出的模拟信号进行简单运算,得到只含角度θ的正余弦值和正切值;然后对得到的正余弦函数进行修正,得到角度θ所在的范围。
将得到的正弦和余弦函数进行区间范围的判断,sinθ和cosθ所在的区间范围如下:当|cosθ|-|sinθ|≥0,θ在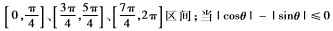

定义一个中间变量α,则有:
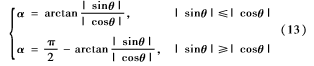
sinθ、cosθ在不同区域的值如表1所示。

上述输出角度θ的划分修正,将角量全部转换到0,π4,可有效避免讨论sinθ或cosθ等于0的情况,在计算过程中,也避免了反正切函数在±π2和±π附近角度不收敛无法计算的情况,因此不占用和浪费大量资源,提高了运算速度。
3.2CORDIC求全角量反正切
对于自整角机输出信号,在旋转的角度一定时,可将输出的信号理解为励磁信号Eref=ERLO-RHIsinωt对sinθ和cosθ进行的幅度调制[6],而励磁信号的变化只是幅值发生变化,对自整角机输出信号的正确解码不产生影响,只要能正确地解码出角度值,则幅值的变化可以忽略不计,本文选择CORDIC算法的矢量模式,令Uxin=cosθ,Uyin=sinθ,z0=0,经过n次迭代后得到式(11)。
3.3CORDIC算法的角度输出
自整角机解码算法采用20位二进制数表示输出信号,输入信号为16位二进制数。1°=216360≈18210=101101102;arctan(2-n)可表示为2202π·arctan(2-n),当迭代次数n不少于16时,就能够达到一定的精度。
4CORDIC自整角机解码算法的实现及仿真
4.1CORDIC自整角机解码算法的实现
基于CORDIC算法实现的设计有迭代结构和流水线结构[7],流水线结构运算速度比迭代结构快,采用流水线结构可有效提高算法速度。在流水线结构中,旋转角度集的各个值均是直接联到累加器的[6] 。流水线结构如图3所示。

4.2FPGA实验仿真
采用VHDL语言描述并在FPGA上实现流水线结构的CORDIC解码算法,利用QuartuesII进行仿真,验证其可行性与正确性。
设定系统时钟为98 MHz,输入一位时钟信号clk,1位使能信号ena,16位输入信号Xin、Yin,及20位角度解码信号输出Aout,仿真选取50°和260°进行模拟,验证该解码算法的正确性。
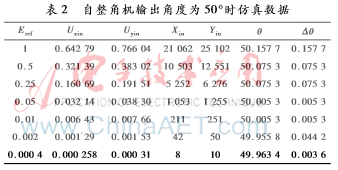
当自整角机的角度为50°时,QuartuesII仿真图及仿真数据如图4和表2所示。

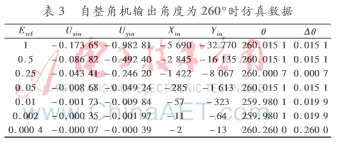
当自整角机的角度为260°时,仿真图及仿真数据如图5和表3所示。

由上述数据可知,在角度一定、Eref变化的情况下,该算法可以正确地解码θ,并且达到一定的精度;仿真中的冒险竞争不是发生在时钟上升沿,不影响角度的正确解码。从仿真图上可以看出有一定的延时,这是由迭代运算造成的效果,可以通过改变时钟频率进行改善。
5结论
本文采用CORDIC算法在FPGA上实现自整角机输出角度的解码,并对自整角机的输出信号进行简单的运算和角度的象限修正预处理,在可计算的范围内,通过QuartuesII验证其可行性与正确性,提升了运行速度和精度,从而验证了该设计的正确可行。
参考文献
[1] 杨桂华. 高精度自整角机精度的分析[J]. 微电机,1990(1):11-15.
[2] 李全.正交三角函数的CORDIC实现[J].微计算机信息,2008,24(12-3):268-269.
[3] 陈石平,廖丁毅,张权.CORDIC算法在正角调制技术的应用[J].广西通信技术,2015(2):49-52.
[4]王华华,陈雷成,陈发堂,等.基于FPGA的STACORDIC算法在SCME中的应用[J].电子技术应用,2014,40(8):109-111,115.
[5] ANDRAKA R. A survey of CORDIC algorithms for FPGA based computers[M]. New York: ACM Press, 1998.
[6] VOLDER E. The CORDIC trigonometric computing technique[J].IRE Transactions on Electronic Computers,1959, 8:379-385.
[7] 李滔,韩月秋.基于流水线CORDIC 算法的三角函数发生器[J].电子技术应用, 2000, 25(4):85-87.

