0 引言

    现今，分布式数据库系统^[1]应用广泛，数据分配对其性能影响极其重要。数据分配问题的描述：假设一个网络由站点集S=(S₁，S₂，…，S_n)构成，该网络上执行一个事务集T=(T₁，T₂，…，T_q)，存储着一个数据片段集F=(F₁，F₂，…，F_m)，按照一定的方式将每个片段F_j的不同副本分配到不同的站点S_k上，分配方案表示为D<F，S，T>。若能够从总分配方案中得到一种较优化的分配方案,整个分布式数据库系统的性能、可靠性都将会大大地提升。

1 研究现状

    目前在国内外有许多文献对数据分配问题进行研究。基于得益代价优化的启发式分配方法^[2]设计复杂，计算开销大；文献[3]提出了基于数据片段访问特性的分配策略，但该策略不能解决搜索容易陷入局部最优解的问题。一些学者利用遗传算法(Genetic Algorithm，GA)来解决数据分配问题^[4-6]，其中文献[6]提出了基于遗传算法的数据分配方法，具有全局搜索能力，能够避免陷入局部最优搜索，但搜索过程是随机的，缺乏记忆功能，搜索速度较慢，且所求结果与最优解有一定差距。

    二进制粒子群算法^[7](Binary Particle Swarm Optimization，BPSO)具有记忆功能，能够提高搜索速度。本文对遗传算法稍加改进，并结合二进制粒子群算法，针对分布式数据库数据分配的代价公式与适应度函数，提出了一种基于混合二进制粒子群与遗传算法(Hybrid BPSO and GA，HBPSOGA)的数据分配方法。

2 基于HBPSOGA的分配方法分析

2.1 统计信息与代价公式

2.1.1 本文采用的统计信息

    统计信息是解决数据分配的基本信息，用于计算检索代价、更新代价和个体适应度。根据统计信息的重要性、获取的难易程度以及对代价公式复杂度的影响，获取表1中的统计信息。

2.1.2 代价公式的选择

    代价的度量标准是Min(TotalCost)。假设各个站点有相同的处理能力，则用访问的总数据量来表示代价公式，所以本文采用的代价公式为：

其中，片段F_j是在站点S_k上的执行事务T_i所访问的数据片段，S_f为F_j的任一副本所在站点，即所有拥有数据片段F_j副本的站点。

2.2 遗传算法及改进

    遗传算法是一种模拟生物学的遗传和进化演变过程所建立的全局性概率搜索算法。由于运用经典的遗传算法来解决数据分配问题，未能快速地找到最优分配方案。因此本文对经典的遗传算法做如下改进：

    (1)在初始化种群时，首先计算数据片段的更新检索比，再基于数据片段的更新检索比来初始化群体。通过式(4)和式(5)分别计算片段的检索访问量和更新访问量：

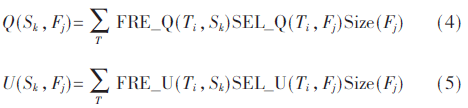
    将所有站点对片段F_j的检索访问量相加得到的值为Q，将所有站点对片段F_j的更新访问量相加得到的值为U。若数据片段中U/Q<1，则在初始化群体时，需要多设置其副本分配给站点，以减少检索通信代价；若数据片段中U/Q>1，则需要少设置其副本，以减少多个副本间数据一致性的更新代价。

    (2)个体进行交叉、变异操作时，采用自调整交叉算子和自调整变异算子^[8]，分别如式(6)和式(7)，能够提升算法的搜索速度和求解质量。

2.3 二进制粒子群算法

    粒子群算法是一种模仿生物种群(鸟群和鱼群)觅食行为的搜索算法。然而标准PSO算法是只适用于连续搜索空间计算，对于离散的搜索空间，它无法直接使用。因此研究人员提出了粒子群算法的二进制版本(BPSO)，用来求解离散二进制空间的问题。

    二进制PSO算法的速度更新公式为：

    为了表示速度的值是位置取1的概率,速度的值被映射到区间[0，1]，映射的方法采用式(9)Sigmoid函数：

2.4 基于HBPSOGA的数据分配方法

    二进制粒子群算法结构简单，运行速度快，具有记忆功能，但容易陷入局部最优，出现了所谓的早熟收敛现象。而遗传算法具有大范围的搜索全局能力，不容易陷入局部最优，但是搜索速度较慢，缺乏记忆功能。本文在基于改进的遗传算法的数据分配方法基础上，引入二进制粒子群算法，提出一种混合算法的数据分配方法，既增强了搜索速度，又避免陷入局部最优，提高成功率。

    针对每个数据片段,采用本文的HBPSOGA获得该数据片段的分配方案,最终得到整体分配方案。下面详细介绍针对某个片段运用该方法进行分配的具体步骤：

    (1)参数初始化，包括最大迭代次数N_max，种群规模PopSize，最大速度v_max，粒子群惯性因子w，学习因子c₁、c₂。

    (2)计算数据片段的更新检索比，基于数据片段的更新检索比来初始化群体Pop=(x_ij)_N×m，其中N为PopSize，即个体的数目，m为所求问题的维数，即站点数目；每个个体采用二进制编码，编码长度等于站点的数目，当在站点S_j上分配数据片段时，x_ij=1，否则x_ij=0。

    (3)定义个体的适应度为：

式中：T_Q、T_U表示查询总代价和更新总代价，详情参见式(2)、式(3)。

    (4)计算种群Pop中的所有个体适应度，采用精英主义操作来选择个体，产生种群Pop′。其精英主义操作是保留适应度大的个体，淘汰适应度小的个体。

    (5)计算种群Pop′中所有个体的适应度，并对其进行评价，使用轮盘赌方法选出染色体对，按照式(6)概率Pc进行交叉操作，得到种群Pop″。其交叉操作是随机设定一个交叉点，两个个体的基因在交叉点位置进行互换，生成两个新的个体。

    (6)对种群Pop″中的个体，按照式(7)概率P_m进行变异操作，得到种群。其变异操作是：个体的基因若为1，则变成0；若为0，则变成1。

    (7)计算种群中的所有个体适应度，得到个体最优位置Pbest和全局最优位置Gbest，并按照式(8)和式(10)分别对种群所有个体的速度和位置进行更新，产生种群Pop。

    (8)若迭代次数已经达到最大迭代次数Nmax，则算法结束，转步骤(9)，否则转步骤(4)。

    (9)输出最优个体作为问题最优解。

3 实验与分析

3.1 实验环境

    在实验中，采用了3种分布式环境。第一种环境含有2个分片、3个事务、4个站点。第二种环境含有3个分片、3个事务、5个站点。第三种环境更为复杂，含有10个分片、5个事务、10个站点。若分布式环境中有n个片段，m个站点，则分配方案有(2^m-1)ⁿ种。因此在这3种环境下，数据的分配方案分别为225种、29 791种、(1 023)¹⁰种。

    在每种分布式环境下随机生成一组统计信息，根据每组统计信息分别使用枚举法的分配方法、本文的分配方法和基于遗传算法的分配方法来进行数据分配，并计算出检索和更新的总代价，统计分配方法所运行的时间。枚举算法的分配方法是循环所有的分配方案，目的是得到最优解的分配方案，进而与本文提出的分配方法和基于遗传算法的分配方法进行比较。基于遗传算法的分配方法是参考文献[6]。3种数据分配方法都是在同一机器上运行比较，机器的配置：CPU i3-2323M 2.20 GHz，内存4 GB。

3.2 实验分析

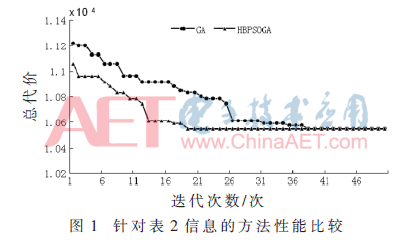
    针对第1组统计信息(见表2)，采用本文的分配方法进行数据分配时，设参数取值如下：PopSize=5，w=0.8，c₁=c₁=2，vmax=4，Nmax=50。

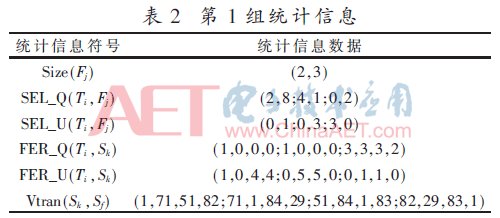
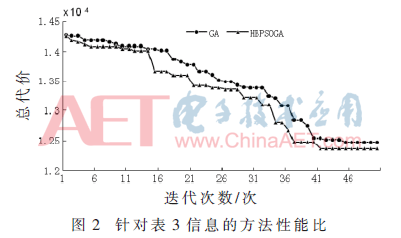
    针对第2组统计信息(见表3)，采用本文的分配方法进行数据分配时，设参数取值如下：PopSize=6，w=0.8，c₁=c₁=2，v_max=4，N_max=50。

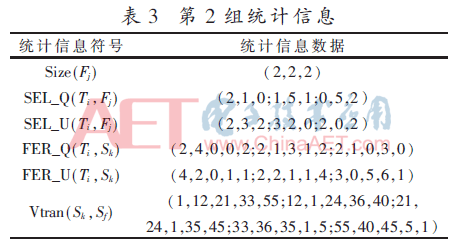
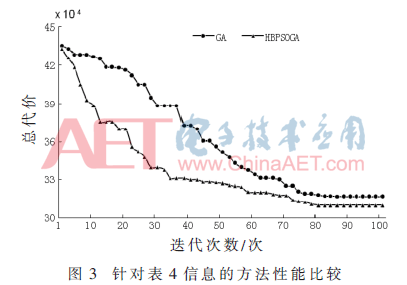
    针对第3组统计信息（见表4），采用本文的分配方法进行数据分配时，设参数取值如下：PopSize=11，w=0.8，c₁=c₁=2，v_max=4，N_max=100。

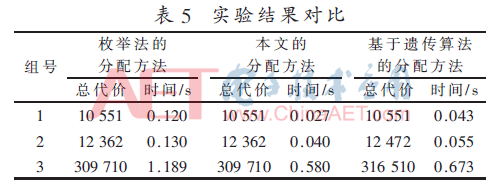
    对3组统计信息进行实验，得到实验结果如表5。在得到总代价方面，本文提出的分配方法和枚举法的分配方法一样，能够得到最小总代价的分配方案。而基于遗传算法的分配方法无法做到。在时间花费方面，本文的分配方法运行时间最短。将本文的方法和基于遗传算法的方法在每次种群迭代时进行性能比较，结果如图1、2、3所示，可以看出，基于HBPSOGA的方法比基于GA的方法获得的总代价值更小，并且在相同的总代价值情况下所运行的迭代次数更少，这说明基于HBPSOGA的方法搜索速度更快。实验表明，采用本文的方法所得到的解是最优解，并且能更快地搜索到最优解。这说明本文采用的分配方法要比枚举法的分配方法和基于遗传算法的分配方法更优。

4 结束语

    本文分析了遗传算法和二进制粒子群算法各自的优点，并对遗传算法稍加改进，在解决分布式数据库数据分配问题上，提出了基于混合二进制粒子群与遗传算法的数据分配方法，通过实验测试了该方法在数据分配方面效果。在获得最优解和搜索速度等方面，分别与枚举法的分配方法和基于遗传算法的分配方法做了比较。实验结果充分说明该方法相比其他两种方法具有搜索效率更高、求解速度更快等特点，并且能够获得全局最优解。

参考文献

[1] 赖玲.分布式数据库系统研究[J].软件导刊，2009，8(9)：169-170.

[2] ISMAIL O H，MUTHU R，NICHOLAS B.A high-performance computing method for data allocation in distributed database systems[J].Springer Science，2007，39(1)：3-18.

[3] 杨洲.分布式数据库中数据分配策略的研究[D].哈尔滨：哈尔滨工程大学，2007.

[4] RAHMANI S，TORKZABAN V，T.HAGHIGHAT A.A new method of genetic algorithm for data allocation in distributed systems[C].Education Technology and Computer Science，First International Workshop on.Wuhan，Hubei：IEEE Press，2009.

[5] PORTALURI，PISA G U，ITALY.A power efficient genetic algorithm for resource allocation in cloud computing data centers[C].Cloud Networking(CloudNet)，2014 IEEE 3rd International Conference on.Luxembourg：IEEE Press，2014.

[6] 李想.分布式数据库数据分配策略研究[D].大连：大连理工大学，2009.

[7] 陈希祥，邱静，刘冠军.基于混合二进制粒子群_遗传算法的测试优化选择研究[J].仪器仪表学报，2009，30(8)：1674-1680.

[8] 赫琳，马长林.改进的自适应遗传算法及其性能研究[C].哈尔滨：中国控制与决策学术年会，2005：895-898.