文献标识码: A
DOI:10.16157/j.issn.0258-7998.2016.07.036
中文引用格式: 王川川,孙霞,钱辉,等. 基于电压自寻优扰动的光伏MPPT算法[J].电子技术应用,2016,42(7):142-145.
英文引用格式: Wang Chuanchuan,Sun Xia,Qian Hui,et al. Study on MPPT of self seeking optimal perturbation method[J].Application of Electronic Technique,2016,42(7):142-145.
0 引言
能源是推动世界经济发展和繁荣的车轮,由于化石燃料产量的急剧下降,如何寻求可替代的可再生能源成为世界各国共同聚焦的问题。作为一种无污染和取之不尽的能源,太阳能在过去的二十年中,已经吸引了更多的关注。由于光伏发电系统组装成本太高,提高效率才是促进光伏产业发展的关键[3],MPPT算法的改进自然成为国内外学者研究的热点。MPPT传统使用的方法包括恒压法、扰动观察法、电导增量法等。其中扰动观察法包括电压扰动观察法和占空比扰动观察法,该方法控制原理简单,但是在最大功率点附近存在严重的振荡问题[1-5];电导增量法[10]精度高并通过修改逻辑判断式可以有效减小振荡,但步长和阈值难以选取,环境突变时可能会发生误判。对于新颖的模糊控制方法,由于直接采用了控制规则表,所以跟踪迅速快、波动小、动态稳定性好,缺点是控制方法的设计缺乏系统性,对于控制目标无法定义,周期太长、成本较高[1],设计难度相对较大。
在对以上传统光伏MPPT分析研究的基础上,本文提出一种电压自寻优扰动MPPT算法。该算法融合了扰动观察法、恒定电压法的优点,并结合了大步长扰动法和小步长扰动法[1],可根据外界环境变化自动调整步长,不断更新初始最大电压Um的值,有效克服了文献[1]所提扰动法由于给定电压不准确带来的误跟踪问题。利用MATLAB/Simulink仿真平台搭建光伏电池模型,仿真结果表明该方法具有兼顾响应速度和控制精度的优点,在最大功率点附近能够实现稳定跟踪,提高了最大功率点的精度及稳定性,减少能量损失[2]。
1 光伏电池数学模型
图1所示为光伏电池等效模型电路,并联电阻Rsh为等效漏电阻,Rs为光伏电池等效串联电阻。
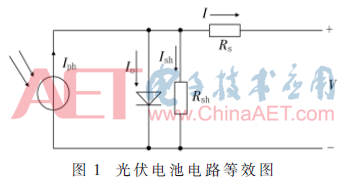
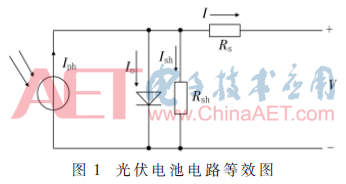
由电路原理易得光伏电池输出电流为:
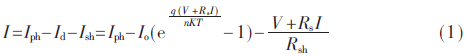
式中,短路电流用Iph表示,二极管饱和导通电流为Io,二极管常数表示为n,q为电子所带电荷(1.6×10-19 C),K为玻尔兹曼常数(1.38×10-23 J/K)。上图中等效漏电阻Rsh一般阻值较大,因此通常情况下我们忽略其影响,且Rs相对于二极管导通电阻可以忽略,简化可得:

一般情况下Rs远小于二极管正向导通电阻,因此设定Iph=Isc,当处在最大功率点和开路状态情况时,必须要考虑电压与电流的关系。在最大功率点条件下:U=Um,I=Im,开路状态下:U=Uoc,I=0,综合以上对光伏电池数学模型的分析,可化简得到式(3):

其中:a=0.002 5/℃、b=0.5、c=0.002 88/℃、e为自然对数。根据所得数学模型利用MATLAB中Simulink工具搭建了光伏电池仿真模型,如图2、图3所示。
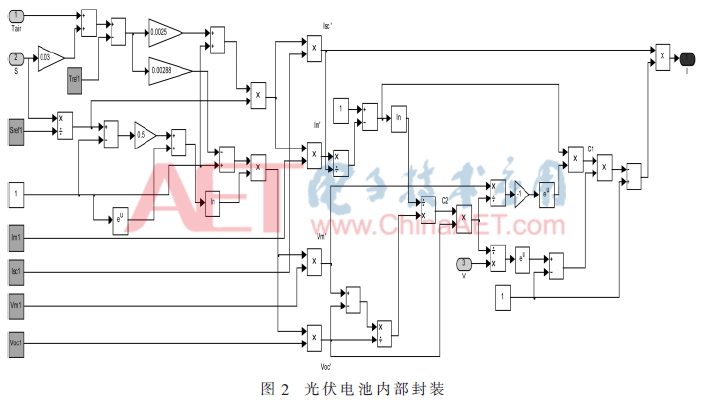
厂家提供的主要参数为Isc=3.90 A,Uoc=21.6 V,Im=3.45 A,Um=17.4 V,其标准功率约为60 W。经仿真得到在标准温度不同光照强度及标准光照强度不同温度的I-U、P-U特性曲线,如图4所示,仿真图形结果跟厂家提供参数一致[4-6]。

2 改进MPPT算法
传统扰动观测法原理简单、实现容易,但在最大功率点处波形震荡明显且经常出现误跟踪,从而导致出现严重的功率损失问题。此外,若扰动步长越大,稳态时振荡范围越大,能量损失越严重,如果扰动步长太小,对于外界环境的变化不能做出快速响应[6]。为了兼顾跟踪速度和精度的要求,本文融合了扰动观察法、恒定电压法的优点,并结合了大步长扰动法和小步长扰动法,提出了一种电压自寻优扰动观察法。该方法首先根据恒定电压法原理,即当温度一定时,光伏电池的最大功率点近似排列成一条直线,如果近似用一条垂线代替这条直线,即保持电压为恒定值,则光伏电池的最大功率输出点近似等于某一恒定电压Um[9],然后测算采样点电压Uk与Um的差值,判断两个电压差的绝对值与Δm、Δs的关系。若|Uk-Um|>Δm时选择大步长ΔUm进行扰动,若|Uk-Um|<Δs则选择小步长ΔUs进行扰动,反之以常规步长ΔUc进行扰动。由于恒定电压法选择的Um为近似值,当外界环境变化很大时会产生较大误差,因此在每跟踪到一个最大功率点时要更新给定电压Um的值,即Pk-Pk-1=0时,Um=Uk。这样既能保证算法的快速跟踪效果,又提高了精确度和系统的稳定性。电压自寻优扰动法的算法流程图如图5所示。
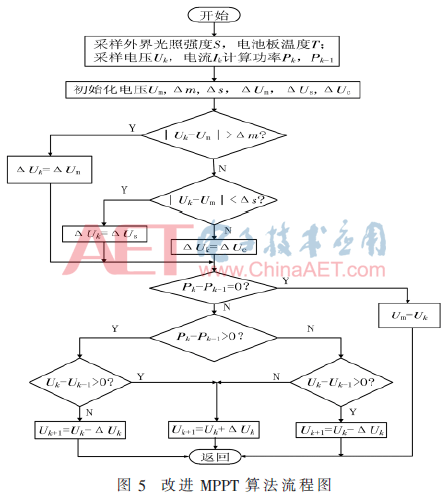
具体控制过程如下:
(1)首先对光照强度S、电池板温度T、电压Uk、电流信号Ik进行采样。然后根据恒定电压法原理得出初始给定电压Um的值,再对参数Δm、Δs、ΔUm、ΔUs、ΔUc进行初始化。
(2)判断采集到的电压Uk跟Um的关系,如若|Uk-Um|>Δm时,选择大步长扰动,即ΔUk=ΔUm,若|Uk-Um|<Δs则选择小步长ΔUs进行扰动,即Uk=ΔUs,否则以常规步长ΔUc进行扰动。这样判据过程可以在保证精度的前提下,提高跟踪速率。
(3)判断当前功率与前一点功率大小,若Pk-Pk-1=0,说明跟踪到了在当前环境条件下的最大功率点,把此刻的电压值Uk赋予全局变量Um,即Um=Uk。当外界环境条件变化时,电压将以新的Um值为中心扰动逼近,可有效提高跟踪精度。
(4)通过判断dP*dU的正负来决定采取正向扰动还是反向扰动[9],若dP*dU>0,说明此时采样点位于最大功率点的左侧,要采用正向扰动,即Uk+1=Uk+ΔUk,若dP*dU<0,此时采样点位于最大功率点右侧,采取反向扰动,即Uk+1=Uk-ΔUk。
3 系统仿真分析
根据如上所述基于电压自寻优扰动MPPT算法搭建了控制仿真模型,boost电路电感值为10 mH,电容值为40 μF,负载电阻值为30 Ω,算法设置为ode45(Dormand-Prince),仿真时间为0.6 s,最大步长为0.01。本实验不仅比较了传统电压扰动法和本文提出的改进型电压扰动法的仿真波形,还观察分析了当外界环境T、S分别变换及同时变化时输出功率波形的变化。
传统扰动观测法及本文提出的自寻优扰动观测法在标准状况25 ℃,1 000 W/m2下输出功率仿真波形如图6所示。
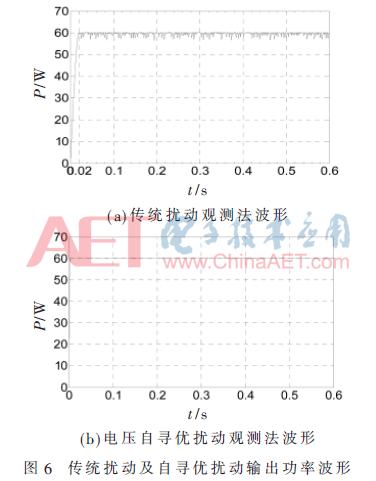
由图6可知传统扰动观测法约在0.02 s时跟踪到最大功率点,而自寻优扰动法约在0.009 s跟踪到最大功率点,跟踪速度得到大幅度提高,且明显减低了波形震荡。
图7所示为当外界环境变化时,输出功率变化波形图,其中图7(a)为光照强度S保持1 000 W/m2不变,而温度在0.3 s时由25 ℃升高到40 ℃时仿真波形图,而图7(b)是相同光照强度下温度在0.3 s降低到15 ℃波形图。图7(c)是温度保持25 ℃不变,光照强度在0.4 s由1 000 W/m2降低到800 W/m2时的仿真波形,图7(d)是在同样温度下光照强度升高到1 200 W/m2时波形。图7(e)为温度在0.3 s由25 ℃升高到40 ℃,而光照强度在0.4 s由1 000 W/m2降低到800 W/m2时的仿真波形图。
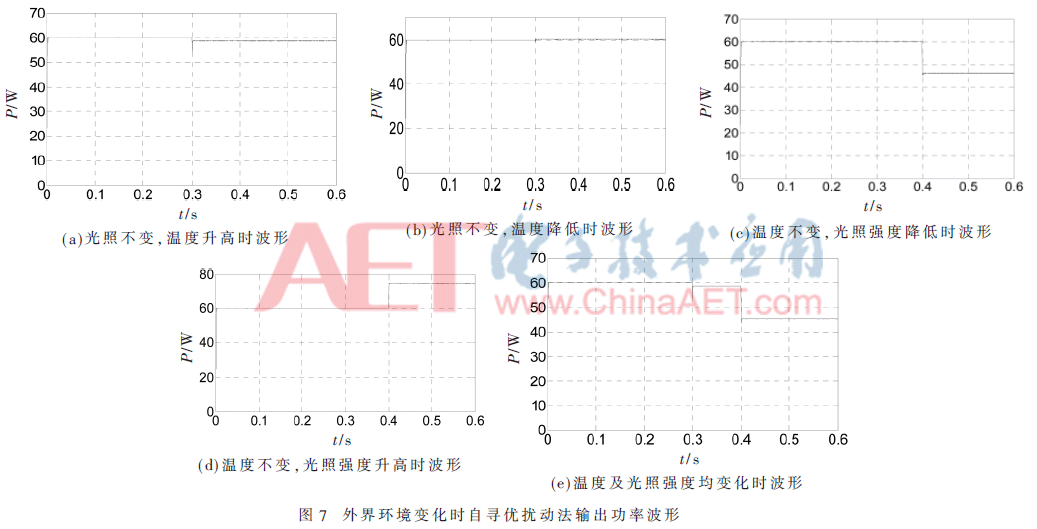
由图7可知当温度升高时,输出功率略有下降,温度降低时,输出功率略有升高。光照强度降低时输出功率降低很大,光照强度增强时,输出功率大幅度升高。因此温度对功率的影响相对较小,光照强度对光伏电池的输出功率影响相对较大。本文提出的电压自寻优扰动观测法对外界环境变化时能做出及时快速的追踪,且波形畸变率小。
4 结论
光能的有效利用是解决能源危机的有效措施之一,最大功率点跟踪技术(MPPT)又是提高光能利用效率的关键。本文提出的电压自寻优扰动观测法融合了恒定电压法、扰动观察法的优点,克服以往初始电压值给定不变的缺点,并结合了大步长扰动法和小步长扰动法,理论分析可行,并根据原理搭建了Simulink仿真模型,验证了该方法动态响应速度快、波形震荡较小、跟踪精度高,具有很高的工程实用价值。
参考文献
[1] 孙志松.光伏并网发电系统的MATLAB仿真研究[D].南昌:南昌航空大学,2012.
[2] 马刚,白凡,蒋林洳,等.基于自寻优占空比的光伏系统最大功率跟踪算法[J].可再生能源,2015,33(5):719-724.
[3] 李雅梅,隋瑒.一种改进的光伏电池最大功率点跟踪控制方法[J].电源技术,2015,39(7):1416-1418.
[4] 周东宝,陈渊睿.基于改进型变步长电导增量法的最大功率点跟踪策略[J].电网技术,2015,39(6):1491-1498.
[5] 安云鹏,刘金宁,赵锦成,等.基于改进电导增量法MPPT控制仿真研究[J].电子技术应用,2015,41(3):130-132.
[6] 王亚楠,杨旭红,王军成,等.一种新型变步长光伏最大功率点跟踪控制策略[J].电气传动,2015,45(1):54-57.
[7] 黄悦华,饶超平,王飞,等.基于SVM改进扰动法的MPPT研究[J].电源技术,2015,39(3):529-532.
[8] 李丽芳,江冰,吉正洵,等.光伏发电系统MPPT控制仿真模型[J].计算机仿真,2015,32(4):116-119.
[9] 王亚兰,陈渊睿.光伏电池通用模型及自适应 MPPT控制方法[J].电源技术,2015,39(1):75-77.
[10] 高嵩,马红利,何宁,等.改进MPPT算法在光伏发电系统中的应用[J].电测与仪表,2015,52(8):120-124.

