0 引言

　　GPS又称为“卫星测时测距导航全球定位系统”，由24颗高度约20 000 km的人造卫星组成[1]。24颗卫星专门用于定位，分布在以地球为中心的六个轨道面上（每轨道面四颗），能够提供24小时连续的定位和导航服务，其接收终端具有定位、授时的能力[2]。目前，GPS在定位上应用较普遍，定向、测姿的应用在起步阶段，存在以下问题：

　　（1）功能单一、大部分只具有定位功能，不能够定向和测量载体姿态[3]。

　　（2）价格相当昂贵。大部分定向、测姿态设备采用惯性导航系统[4]，价格超过100万元。

　　（3）输出信息不具有二次开发性。

　　（4）信息输出不具有实时、可靠、准确、快速性。

　　（5）坐标输出信息不全，与外接设备无信息交换。

　　因此，研究一种集定位定向、测姿功能的系统十分必要。

1 GPS定向测姿相关理论研究

　　1.1 利用载波相位测量建立误差方程

　　GPS卫星信号接收机有很多种类,一般都有两类基本的观测量:一个是伪距观测量，另一个是载波相位观测量[5]。

　　GPS载波分为：L1，其波长为0.19 m，频率为1 575.42 MHz，观测误差为1.9 m[6]。

　　设GPS的卫星j在t0时刻发射信号，经过时间t后于ti时刻被GPS终端机接收，为t对应的相位差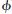，j(ti)为GPS卫星载波信号在t时刻的相位，i(ti)为接收机本地信号在时刻的相位，则：

　　其中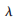为波长。

　　卫星与接收终端机之间的相位差一般由整数和小数两部分组成：

　　其中，N0为整周相位数，为不足一个整周相位部分。

　　在接收机的鉴相器中，只能测出小数的部分。

　　ti时刻GPS卫星到接收机的载波相位为：

　　其中，N0为载波相位测量中出现了一个整周未知数。接收终端机锁定并实时跟踪卫星信号后，并不断测定载波相位的变化，在ti时刻利用多普勒计数器记录，Nk为ti时刻到tk时刻相位整周变化量。

　　载波相位测量只能测量小数部分，原因有多种，其中可能产生整周跳变现象，例如接收机天线被遮挡、卫星数量过少、信号丢失、外界噪声信号的干扰等。理论上可以通过数据处理如滤波来解决一些问题，但滤波是有代价的，数据不能实时反应载体的运动状态，实现也很复杂[7]。

　　在实际应用中，如GPS应用在车上、船舶、飞机等载体，GPS接收机由于多路径误差、时钟等多种信号经常在非真空中传播，会遇到不同的复杂情况，还可能出现电离层、对流层延时误差、接收机测量噪声等多种原因，造成GPS载波相位测量中存在着误差[8]。误差测量方程为：

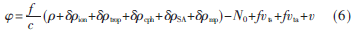
　　1.2 GPS定位技术理论分析

　　GPS定位分为绝对定位和相对定位，即为单点定位和差分定位，精度要求较高，尤其是大地测绘或军事应用采用相对定位，一般精度都在厘米级，需要8个以上的通道才能够保证精度，跟踪卫星超过7颗。

　　基本观测方程为[9]：

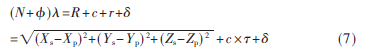
　　其中，为相位观测量；R为接收机到卫星的距离；r为接收机钟差；为对流层和电离层的延迟。式(7)中，?准是相位小数，N是相位整周数信号通过对流层、电离层的延迟修正；(Xs，Ys，Zs）为卫星的瞬时相对于地心坐标；(Xp，Yp，Zp)为接收终端机到地心坐标。

　　GPS终端机的接收天线假如安装在T1、T2两个固定点或测站上，它们在同一时刻同时观测到星历数据[10]，利用数据处理单元记录并建立相位观测量，从而得到基本单差观测方程：

　　上标为卫星号，下标为测站号，由此可以看出，利用同一时刻观测的两颗卫星的单差方程式来求解双差(DD)的观测方程。

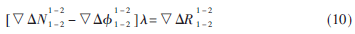
　　式(10)双差观测方程中是基线向量与相位整周数差值部分。相位整周数一般情况不会发生变化，不受时间和地点发生变化。可以根据相邻两个双差观测方程得到三差观测方程。

2 GPS定向测姿系统实现

　　利用车辆的航向、横滚、俯仰描述车体运动是基于真北向与水平位置的关系，其中载体航向是载体基于地理坐标系中载体中轴线与真北向的夹角称为航向。车辆坐标X、Y、Z是游动坐标系(b系)和地理坐标系(n系)之间坐标转换，其方位与它们有一个夹角关系[11]。因此，地理坐标系为北东天地坐标系，游动坐标系xb轴指向车辆前进方向，也就是说我们载体的航向，yb指向车辆的前进方向车辆侧面，也就是说载体的横滚；zb指向车辆的底盘下方，这样就构成了东北天地的坐标系。则航向角以北向向东向偏转为正，反方向为负；俯仰角?兹以向上为正；横滚角以载体坐标系xb轴方向为正，相反为负[12]。

　　游动坐标系和地理坐标系之间的转换矩阵为：

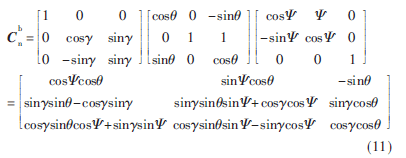
　　C为姿态矩阵，是地理坐标系和游动坐标系之间的方位关系。

　　俯仰角的取值范围在±90°范围内，与三角函数中的反正弦函数值一样，有区间问题，但值只有正负之分。而航的定义域为0°～360°区间内，横滚角的定义域为-180°～+180°区间，所以得到求解的姿态角存在象限判断问题，判断方法如表1、表2所示。

　　2.2 GPS单基线方位角解算及误差分析

　　所谓单个基线就是只有一条基线，本论文利用6 m长的基线，解算航向和俯仰。一条基线沿载体的纵轴安装，解算出航向角和俯仰角，如果再加一根基线只沿载体的横轴安装，则可以解算出横滚角，本论文采用单基线三个GPS的安装方法[13]。

　　将基线沿载体的实际中轴线安装，也就是说基线向量在车辆坐标系中的坐标表示为Rb=[b 0 0]T，b是基线长度，单位为m，本论文中基线的长度设计为6.00 m，基线向量在地理坐标系中的坐标为Rn=[xn yn zn]T，则根据式(13)并根据姿态矩阵C的正交性，可以得到航向角、俯仰角的估计值：

　　其数值的范围为：

　　由上推出，航向角及俯仰角的解算精度与基线的长度成反比，理论上基线越长精度越高，但是，选择的GPS基线长度不可能无限长，我们只能在合理的区间选择。通过固定基线，求解航向、姿态，直接由XDOP、YDOP、ZDOP作为对角线元素构成的对角矩阵称为姿态精度因子矩阵。

　　2.3 GPS双基线姿态解算方法

　　如果有三个或多个不共线的GPS接收机天线，组建成互相垂直的两条基线，这两条基线可以在自己的坐标系内，通过信号接收板接收到4颗以上卫星，就可以联立方程解算出全部载体的航向、横滚、俯仰角。本小节利用基本算法解算姿态矩阵C，从而解算出姿态参数。

　　两条基线安装车体上，在游动坐标系中的坐标中设为Rb1、Rb2，在地理坐标系中的坐标设为Rn1、Rn2。

　　通过建立三个互相正交的矢量，联立求解，分别为：

　　同样可以在地理坐标系中建立三个互相正交的矢量：

　　如果两个基线向量不平行，所以矩阵从满秩，是可逆的，由式(24)可以解算出姿态矩阵：

　　从而解算出三个姿态角，即航向、横滚、俯仰。为了减少误差，尽量保持两条基线垂直，用转角直尺来校准；基线长度按需求尽量长，一般采用6 m基线，测量基线长度采用多测几次求平均值的方法；解算采用双精度浮点运算。

3 利用最小乘法求解整周模糊度及姿态确定

　　采用了三个GPS接收天线，并将天线安装一根长度为6 m的铝合金基线上，天线安装需在同一条直线上，其中两个最短的GPS接收天线相距14 cm，用于粗寻北，最长的两个GPS接收天线相距6.00 m，用于精寻北。当卫星数据超过4颗时，10 s内解算出直线的初始方向，1 min内确定初始模糊度，以此确定搜索范围，快速搜索出拟合残差小于给定值的阈值内解的集合，最后确定拟合残差优选出最优解[14]。

　　3.1 GPS模糊度的搜索范围

　　卫星空间布局确定搜索范围，双差方程可以写为：

　　Qi=Hi1X1+Hi2X2+Hi3X3+Ni(26)

　　要求其N的范围，只须求出H1 X1、H2 X2、H3 X3的范围，由于：

　　根据求条件值理论可以求得：

　　求解确定模糊度范围，把模糊度看作待求值，由式(26)中的双差型方程，可以改写为：

　　由式(26)、式(29)求交集可以得出模糊度N的范围。

　　3.2 GPS模糊度的最优判定及载波整周数

　　模糊度的最优判定是一个难点。由于卫星信号在传输过程中的各种干扰和接收机本身的噪声，使得有时真值不一定是最优解。

　　根据数理统计理论：次优残差平方和与最优残差平方和之比服从χ2分布。模糊判断如下：

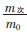　　≈x2，判别准则为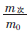：>k则判最优解为真值；<k则需要延长时间重新计算。k值的取值需要遵循数理统计规律和实际测试情况综合确定。

　　载波整周数：相位测量?兹i，最小的ni和X，根据最小二乘拟合计算X。

　　3.4 快速确定航向

　　根据一点坐标和方向矢量，进行坐标转换可以确定北向方向。

　　(1)求A=(X1，Y1，Z1)T的地心坐标求解A点的经度。

　　4 实测验证

　　GPS定位测姿系统与测绘局测量的标准点对比测量定位精度，多次测试航向、俯仰重复性精度，动态测量采用测绘局实测标准点与惯性导航测量姿态结合测量定位、定向、俯仰精度。

　　4.1 定位情况及结果对对比图

　　验证GPS定向测姿系统定位精度，采用测绘局实测标准点为基准，精度在10 cm内，在卫星信号达到7颗以上的情况实测10 min，GPS定位测姿系统采用差分方式，CEP精度高于5 cm；GPS单点定位CEP精度超过10 m。测试结果如图1，单位为度。

　　4.2 转台测试情况及结果

　　将GPS接收天线基线固定高精度转台上，基线长6 m。在不同的方向上连续测试。试验结果符合技术要求。见表3。

　　4.3 动态跑车实验结果

　　将GPS的6 m长的基线架在车上，基线安装在车的中轴线上，先标定基线与车中轴线的安装夹角后，然后进行实验。以高精度差分GPS为标准测量其定位精度，以高精度航姿设备为标准(精度超过0.1 mil)，标安装误差后，连续多次动态实验结果，经过多次动态实验结果详见表4。

　　从上表实验结果说明该系统动态定位精度、动态航向精度与标准系统航向误差小于1 mil。

5 总结

　　通过对GPS技术应用研究，运用载波相位测量原理、定位技术理论分析、卫星位置计算等相关理论知识，建立定向测姿系统载波相位观测方程，分析了单基线方位角解算及误差，推导了利用单基线解算方位角和俯仰角以及利用双基线解算全姿态角的方法，提出整周模糊度快速解算的新方法，利用三角函数约束条件减少整周模糊度的搜索范围，筛选指标不受基线运动的状态影响来进行平差，以及利用最小二乘法用于整周模糊度问题快速确定模糊度范围、模糊度的搜索及其模糊度的最优判定，最后计算出最优解，达到GPS快速确定最优航向和俯仰角效果。

参考文献

　　[1] 范胜林.GPS姿态及定向系统的研究与实现[D].南京：南京航空航天大学，2001.

　　[2] 王惠南.GPS导航原理与应用[M].北京：科学出版社，2003：206-243.

　　[3] Kendall Ferguson，Joanna Kosmalska，Hark kuhl，et al.Three-Dimensional attitude detemination，with the ashtech 3DF 24-channel GPS Measurement System[C].Proceedings of 47th Annual Technical Meeting on Using Synergism to Strengthen Navigation System 1991：35-41.

　　[4] 陈小明.高精度GPS动态定位的理论与实践[D].武汉：武汉测绘大学.1997.

　　[5] 黄丁发，卓健成.GPS相位观测值周跳检测的小波分析法[J].测绘学报，1997，6(4)：352-357.

　　[6] 胡国辉，孟浩，袁信.差分GPS载波相位测量整周模糊度的快速求解[J].航空学报，1999(2)：127-129.

　　[7] 章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社，1998.

　　[8] 廖向前，黄吉顺，黄晓玲.G玲双基线载体姿态侧量研究[J].肮空学报.1998，19(5)：531-535.

　　[9] 胡国辉，孟浩，袁信.差分GPS载波相位测量整周模糊度的快速求解[J].航空学报，1999(2)：127-129.

　　[10] 李海峰，孙付平.卫星导航接收机测试场景软件的设计与实现[J].中国惯性学报，2008，16(2)：183-187.

　　[11] 廖向前，黄吉顺.一种GPS动态解相位模糊的搜索算法[J].电子科技大学学报，1997，26(4)：13-17.

　　[12] 逯亮清，胡小平，吴美平.利用旋转基线方法进行双星快速定向[J].宇航学报，2004，25(2).

　　[13] 武静.基于非线性模型的单机GPS定位估计方法的研究[D].上海：上海交通大学，2007.

　　[14] 姚勇，张春.GPS载波相位差分技术实时测姿的研究与应用[J].中国惯性学报，2003，6(3)：21-23.