文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.10.005
中文引用格式： 杜玉龙，李建增，张岩，等. 基于强独特性二进制描述子的无人机目标识别算法[J].电子技术应用，2016，42(10)：24-28，32.
英文引用格式： Du Yulong，Li Jianzeng，Zhang Yan，et al. Objection recognition algorithm of UAV based on strong uniqueness binary description[J].Application of Electronic Technique，2016，42(10)：24-28，32.
0 引言
目标识别是计算机视觉领域内的经典问题，随着多媒体技术的发展，人类接收的信息量与日俱增，使用计算机代替人力实现目标识别已逐渐成为发展趋势。在军事应用方面，为了节省人力以及减少人员伤亡，无人机目标识别技术同样得到了广泛研究，而无人机的迅猛发展为该技术提供了研究条件和工程应用基础。目标识别中特征描述算法可分为浮点型和二进制两类，与采用欧氏距离作为特征点匹配判定条件的浮点型算法不同，二进制算法通过异或操作即可完成判断，有效降低计算量，确保图像的实时处理，考虑到无人机目标识别应用对于实时性的要求，选用二进制算法作为本文算法的基础。
代表性的二进制算法主要包括BRIEF[1](Binary Robust Independent Elementary Features)算法、ORB[2](Oriented Fast and Rotated BRIEF)算法、BRISK[3](Binary Robust Invariant Scalable Keypoints)算法以及FREAK[4](Fast Retina Keypoints)算法等。其中BRIEF算法在特征点邻域内随机选取采样点对，通过灰度对比生成特征描述符，虽然算法运行速度很快，但采样点选取策略的随机性导致算法的特征表达能力有限，且旋转不变性与尺度不变性较差。ORB算法在其基础上引入方向特性，具备良好的旋转不变性，但采样点选取策略并没有得到改进。BRISK算法设计了一种固定采样模型，基于该模型的特征描述有效改善算法对于各种变换的鲁棒性，但模型内采样点感受域之间重叠率低，信息连续性较差，导致特征描述不够充分。FREAK算法根据人眼视网膜原理，在BRISK算法的基础上进一步优化采样模型结构，增加了相邻采样点感受域之间的交叠带，改善了特征描述的信息含量，但重叠区域过大导致信息冗余，降低了描述子的独特性。
针对传统无人机目标识别特征描述算法的不足，提出了一种基于改进采样模型的强独特性二进制描述算法，算法首先对比BRISK和FREAK采样模型，确定影响模型性能的参数，并通过理论建模逐项优化选取参数最优值，根据人眼视网膜中细胞的分布特性得到改进模型。在此基础上，对图像进行灰度划分及排序，将改进模型映射其中，增加对图像层次信息的表达，在众多描述子中选取具有强区分性和低相关性作为最终的特征描述子，改善算法的鲁棒性能。
1 构建采样模型
在特征描述阶段，通过比较采样模型内采样点对的灰度值生成二进制描述字符串，因此合理的采样模型是保证描述子性能的关键。在设计采样模型前，首先对比BRISK和FREAK采样模型以确定影响模型性能的参数，模型示意图如图1所示。
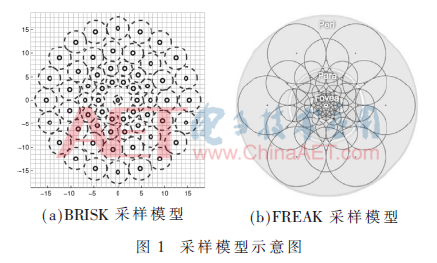
1.1 传统采样模型分析
两种采样模型均采用圆形对称结构。通过对比分析得出影响性能的主要参数分别为：采样点密度、采样环层数和采样点感受域重叠度。
三个参数之间相互联系和制约，由于同一采样环上的采样点之间不存在重叠，采样点密度决定了每个采样点的感受域，相邻采样环之间的距离决定了采样点感受域之间的重叠范围，采样点密度与采样环层数决定了采样模型内的采样点个数，三者之间相互作用共同决定了采样模型的性能。
1.2 采样环层数与采样点密度
首先对采样点全局均匀分布类模型性能进行测试，结果如图2所示。
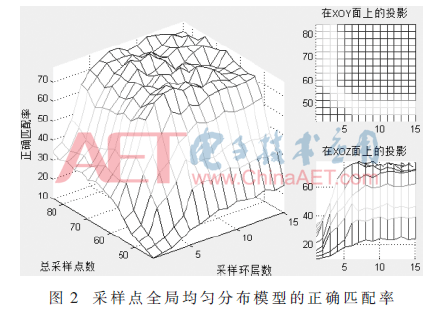
实验结果表明：此类模型的正确匹配率随总采样点数和采样环层数的增加逐渐上升，当采样点数为57个，采样环达到6层时，模型获取的所有信息中特征信息占比最高，描述子位特征方差和均值达到最佳，模型性能最优。为了满足图像实时处理的要求，选取57个采样点均匀分布在6层采样环上的模型作为此类最优模型，基于此模型的算法正确匹配率为74%。
对相同层采样点数类分布模型性能进行测试，结果如图3所示。
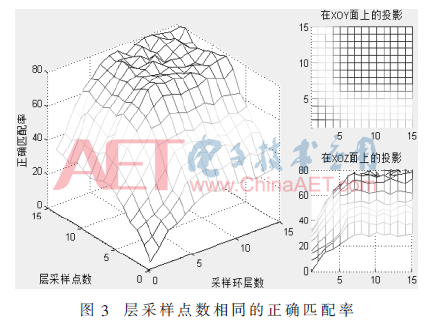
实验结果表明：此类模型的正确匹配率随层采样点数和采样环层数的增加逐渐上升，对应的总信息中特征信息比重逐渐增大，当达到极值时，特征信息利用率最高，算法性能达到最优并逐渐趋于稳定。因此，综合考虑算法的精确度和复杂度，将7层采样环，每层均匀分布8个采样点的模型作为此类最优模型，基于该模型的算法正确匹配率为78%。
1.3 感受域范围重叠度
在生成描述子时，采样点的感受域越大，包含的信息越多，特征点的描述子独特性越强，但过大的感受域会使重叠度增大，从而导致信息冗余。对不同重叠度下模型获取的信息量进行统计，以确定最优重叠度，结果如图4所示，当重叠度为20%～25%时特征信息含量达到极值，因此在设计采样模型时，将每个采样点的感受域重叠度调整为23%左右。
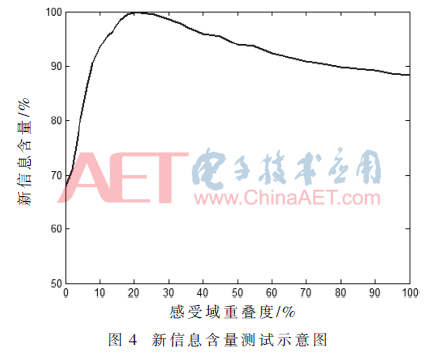
1.4 本文采样模型
研究[4]表明：人眼在观察目标时，通过视网膜中央区域识别目标的细节信息；而周边区域主要用于检测目标的轮廓信息；其细胞分布的数学模型符合高斯分布[8]。根据人眼视网膜中的细胞分布规律，提出一种基于高斯分布的强独特性描述子采样模型。模型性能测试结果如图5所示。
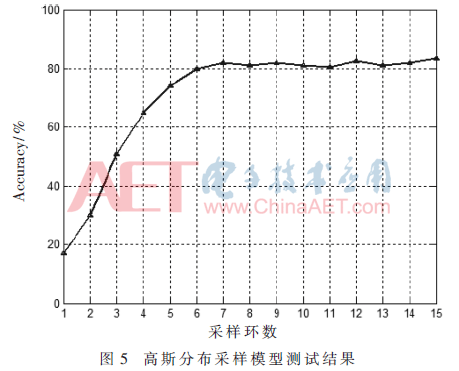
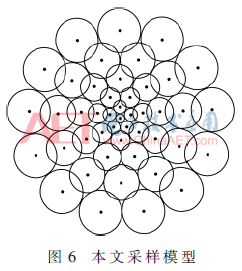根据测试结果，当模型的采样环达到6层后算法性能逐渐趋于稳定，此时的正确匹配率为83%，性能优于前两类模型。根据这一结论得到本文模型分布如图6所示。
2 构建二进制描述子
在传统无人机目标识别特征描述子的生成过程中，仅在特征点的单一邻域内利用采样模型中采样点对比结果生成二进制字符串，缺乏对图像层次信息和旋转信息的表达，且忽略了图像中像素的聚类特征，导致描述子在图像中存在各种仿射变换和噪声干扰情况下的鲁棒性能较差。针对这一局限性，本文在改进采样模型的基础上，通过对图像分层处理提升算法的独特性。
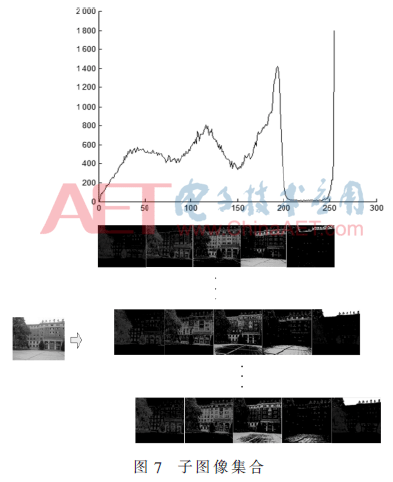
如图7所示，将灰度值划分为几段，对应不同区间可得到多组子图像，分别对每一幅子图像进行多尺度高斯平滑，高斯核越大，特征点的鲁棒性能越强，因此优先描述高尺度平滑子图像特征点，并赋予较高的权重。将通过不同灰度划分计算法得到的描述子在按顺序排列成矩阵形式，分别计算矩阵的方差和协方差，筛选出其中具有强区分性和低相关性的列作为最终的特征描述子。
3 实验分析
为了测试本文无人机目标识别算法的鲁棒性能，采用由Mikolajczyk[10]所提供的国际标准测试图像集进行实验。
3.1 鲁棒性能测试
在测试中统一采用FAST-Hessian算法进行特征点检测，利用Precision-Recall曲线对算法的鲁棒性能进行分析，其中Precision代表查准率，即所有匹配特征点中正确匹配点所占的比例；Recall代表查全率，表示正确匹配特征点数与特征点总数的比值，其计算公式分别为：
其中，#correct matches表示错误匹配的特征点数，#match keypoints表示匹配成功的总点数，#corresponding keypoints表示两幅图像之间对应的特征点总数。采用各个测试集中的第一幅与第四幅图像进行实验，测试结果如图8所示。
图8中测试曲线表明：本文算法在各种变换下的鲁棒性能优于其他四种算法，这是由于采样模型中采样点感受域之间的交互重叠使得模型能够充分获取特征点的周边信息，信息更加连续，保证模型对于视点变换具有更强的鲁棒性。在生成描述子时，对子图像进行了多尺度高斯平滑，并引入灰度排序信息，通过计算描述子矩阵的方差和协方差，筛选其中具有强区分性和低相关性的特征描述子，从而能够更好地克服各种变换对目标识别带来的影响，保证算法在无人机战场侦察中对于各种复杂环境的稳定性能，有利于对于敌方情报的实时掌控，控制战争走向。
3.2 实时性
在测试图像集中，分别统计各无人机目标识别算法的总匹配特征点数Num、特征描述总耗时t和每个特征点描述平均耗时Ave，通过数据对比分析算法性能，统计结果如表1所示。
其中SIFT和SURF算法作为浮点型算法通过计算特征点之间的欧氏距离判断是否匹配，因此耗时严重。而二进制BRISK和FREAK描述算法，只需在特征点邻域内按照采样模型选取点对进行灰度比较，将生成的二进制描述字符串作为特征描述子，因此算法运行速度有较大提升，满足实时性处理的实际应用要求；本文采样模型在设计过程中，通过合理选取采样点密度和采样环层数，按高斯模型分布采样点，优化感受域重叠度，从而增强模型独特性，并提高算法的精度与速度。但本文算法在生成描述子时引入了灰度排序信息，在改善描述子性能的同时，算法耗时相对有所提高，根据表1数据，本文算法耗时在BRISK和FREAK算法之上，但远少于浮点型算法的耗时，基本满足实际应用中实时性的要求，结合识别性能中的测试结果，本文所提出的无人机目标识别算法能够同时满足战场应用对于识别精度和速度的要求，且相对传统算法有较大的提升，因此本文算法具有一定的优越性。
4 结论
针对传统无人机目标识别算法中特征描述子独特性有限导致算法误匹配率较高，目标识别精度较低的不足。本文首先对影响模型性能的主要因素进行分析，然后通过理论建模获取最优参数，结合仿生学原理，提出一种基于高斯分布的强区分性采样模型，最后结合灰度排序信息和高斯平滑，通过计算方差和协方差筛选出具有强区分性和低相关性的特征描述子；实验结果表明本文算法不仅能较好地克服战场侦察图像中各种变换带来的影响，同时满足实际应用中实时性处理的要求。
本文在构建采样模型时，只在两种约束模型条件下进行了讨论分析，进一步优化时可考虑采样模型的所有可能分布，从而获得绝对最优模型，且只对目标识别中的特征描述算法进行了优化，对于特征检测算法的改进可作为下一步研究方向。
参考文献
[1] CALONDER M，LEPETIT V，OZUYSAL M，et al.BRIEF：binary robust independent elementary features[J].IEEE Transactions on Model Analysis and Machine Intelligence，2012，34(7)：1281-1298.
[2] RUBLEE E，RABAUD V，KONOLIDGEK，et al.ORB：an efficient alternative to SIFT or SURF[C].Proceedings of the 13th IEEE International on Conference Computer Vision.Los Alamitos：IEEE Computer Society Press，2011，2011：2564-2571.
[3] LEUTENEGGER S，CHLI M，SIEGWART R.BRISK：binary robust invariant scalable keypoints[C].Proceedings of the 13th IEEE International Conference on Computer Vision.Los Alamitos：IEEE Computer Society Press，2012：2548-2555.
[4] ALAHI A，ORTIZ R，VANDERRGHEYNST P.FREAK：fast retina keypoint[C].Proceedings of Computer Version and Model Recognition.Los Alamitos：IEEE Computer Society Press，2011：510-517.
[5] MARI E，HAGER G，BURSCHKA G，et al.Adaptive and generic corner detection based on the accelerated segment test[C].Proceedings of the 11th European Conference on Computer Vision，2010，6312：183-196.
[6] 惠国保，李东波，童一飞.挖掘图像补丁特征信息增强二进制描述子独特性[J].计算机辅助设计与图形学学报，2014，26(9)：1419-1429.
[7] 白丰，张明路，张小俊，等.快速优化筛选多尺度矩形域的二进制描述[J].中国图像图形学报，2016，21(3)：303-313.
[8] 林森，苑玮琦，宋辉.二进制鲁棒不变尺度特征在非接触掌纹识别中的应用[J].仪器仪表学报，2013，34(12)：2785-2792.
[9] BEKELE D，TEUTHCS M，SCHUCHERT T.Evaluation of binary keypoint descriptors[C].Proceedings of the 20th IEEE International Conference on Image Processing，2013：3652-3656.
[10] MIKOLAJCZYK K，SCHMID C.A performance evaluation of local descriptors[J].IEEE Transactions on Model Analysis and Machine Intelligence，2005，27(10)：1615-1630.
[11] 王灿进，孙涛，陈娟.基于FREAK特征的快速景象匹配[J].电子测量与仪器学报，2015，29(2)：204-212.