0 引言

　　分布式信源编（DSC）解码较传统信道编解码而言，因其编码简单、译码复杂成为近年来通信领域的研究热点。DSC编码端各信源独立编码，译码端根据信源的相关性联合译码，从而降低了编码的复杂度，而把整个系统的复杂度转移到译码端，所以本文重点研究DSC译码器的设计。

　　Turbo码和LDPC码是实现DSC译码器的两种主要编码。在DSC译码过程中，Turbo码译码算法复杂、译码延时长且存在一定的不可检测错误，而LDPC码具有较大的灵活性、较低的差错平底特性、译码速度快、具有高效的译码迭代算法[1]，因此LDPC码更适合于实现DSC译码器。

　　LDPC码分为规则LDPC码和非规则LDPC码，非规则LDPC码的译码性能优于规则LDPC码，是目前己知的最接近Shannon限的码[2]，所以本文采用非规则LDPC码实现DSC译码器。

　　本文设计的DSC译码器具有反馈信道，根据当前联合译码的结果把译码判决信息反馈到编码端，但这种方法对实时性要求很高[3]，这是限制DSC译码器工程应用的一个重要因素。FPGA由于其强大的数据并行处理能力，能够做到数据处理的实时性、高效性。所以，FPGA能够解决DSC译码器反馈信道实时性的问题。

　　Log-BP算法、BP-Based算法、归一化最小和（NMS）算法是3种常用的DSC译码算法，这3种算法把一部分乘法用求和运算代替极大地减少了运算量。Log-BP算法修正了码长较长时概率 BP 译码算法计算不稳定的问题，但是仍然存在乘法运算不利于 FPGA实现。BP-Based算法虽然降低了运算量，但BP-Based 算法相对于Log-BP算法收敛速度慢，译码性能也不如前者[4]。NMS算法和BP-Based算法的复杂度几乎相同，若选取合适的归一化因子η，能将乘法用加法和移位操作代替，并且其译码性能与概率BP算法几乎一致[5]。因此，NMS算法在FPGA实现时被大量采用。

　　基于非规则LDPC码、FPGA、NMS译码算法3方面的优点，本文的主要工作是采用非规则LDPC码、运用NMS译码算法设计了一种全新的、实时高速的DSC译码器并在Xilinx XC7VX485T上实现了该译码器。该译码器的吞吐率可达197 Mb/s，具有较好的工程应用价值。

1 DSC译码器实现的理论基础

　　1.1 DSC的基本原理

　　假设Xi(i=1，2…N)是来自同一个系统的N个信源，这N个信源之间的相关性称为边信息，现对这N个信源进行独立编码，将编码后的N路信息传输到同一个译码节点，并结合边信息进行联合译码。因此，DSC系统的编码端极为简单，其复杂度主要体现在译码端。

　　1.2 基于非规则LDPC码的DSC系统

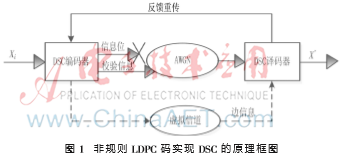
　　图1是非规则LDPC码实现DSC系统的框图，其中Xi(i=1，2…N)表示来自同一个系统的N个信源，DSC编码器和译码器根据非规则LDPC码的校验矩阵（H矩阵）而设计。

　　从图1中可知，非规则LDPC码实现DSC编解码系统的基本原理：信源Xi经过DSC编码器后输出信息位和校验信息，与传统译码相比，DSC编解码系统丢弃信息位并且经高斯白噪声（AWGN）信道每次只传输少量的校验位到DSC译码器，如此可以实现码率自适应并提高压缩效率。同时边信息经过虚拟信道传输到DSC译码器进行联合译码，如果此时能够正确译码就输出译码信息X’，否则进行反馈重传校验位继续译码，直至正确译码输出。

　　1.3 LDPC译码算法

　　NMS译码算法具体阐述如下：

　　设α2为AWGN信道的方差，yi表示接收到的信息，L(ci)为信道初始化信息，L(qij)为变量节点接收来自校验节点的信息，L(rji)为校验节点接收来自变量节点的信息，L(Qi)是变量节点接收到的全部信息，C(i)表示连接变量节点i的所有校验节点，C(i)\j表示连接变量节点i中除j外的全部校验节点，C(j)\i表示连接校验节点j中除i外的全部变量节点，η表示归一化因子。

　　(1)初始化：

　　(2)更新校验节点：

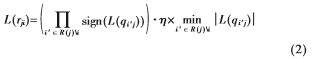
　　(3)更新变量节点：

　　(4)更新L(Qi)：

　　(5)最后，对任意i，有：

　　若变量节点收集到的信息值L(Qi)<0，对任意i，判别译出的码字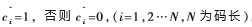。如果H^T c^^=0或者译码的迭代次数等于预设的最大值，c^^也作为最终译码输出，并强制终止译码计算；否则转至步骤(2)继续译码计算。

　　从式(2)中可以看出NMS算法仍然存在少量的乘法运算，若选取合理的η，则能在不损失译码性能的情况下，将乘法用加法和移位操作代替[5]，使译码的计算量最少、译码的复杂度最小、FPGA消耗的资源最少。

　　η是一个小于1的正常数，通常在FPGA上实现LDPC译码算法时选取η为0.75，此时的NMS算法译码性能最佳[6]。

2 DSC译码器设计

　　文献[7]对非规则（2 048，1 024）、码率1/2的H矩阵的研究表明该H矩阵在译码过程中能够实现相当低的误码率。因此本文选用此类型度分布为(λ(x)，ρ(x))，码率为1/2的非规则H矩阵，其中λ(x)=0.285 6x+0.257 5x2+0.456 7 x7，ρ(x)=0.003 4x5+0.996 6x6。

　　本文设计的DSC译码器分为输入模块、缓冲模块、节点信息更新模块、判决模块、控制模块、反馈模块、输出模块。图2是DSC译码器的逻辑结构图，该译码器主要模块的功能如下：

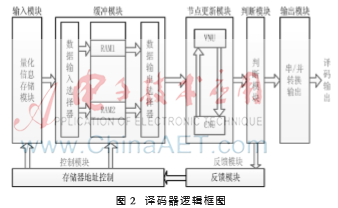
　　(1)将量化好的边信息、校验位信息存入FPGA Block RAM模块中。

　　(2)缓冲模块中两个完全相同的RAM块用于乒乓操作，周期性地切换数据选择器可以提高数据传输的速率、效率，亦能使缓冲模块与节点更新模块的速率相匹配。

　　(3)控制模块用于控制量化信息存储器和缓冲模块的工作时序，保证这两个模块有序工作，保证数据连续。

　　(4)节点信息更新模块控制变量和校验两类节点的信息更新，并将判决信息输出给判决模块。

　　(5)反馈模块把判决结果实时反馈到数据输出选择器端，通知输出选择器继续发送校验信息。

　　该译码器的设计重点体现在节点更新模块、判决模块和反馈模块。图3是这3个模块的工作流程。

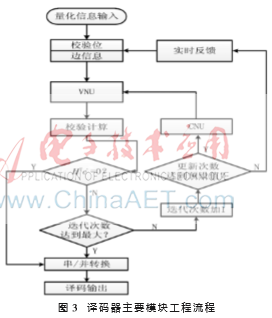
　　2.1 量化位数及迭代次数设计

　　量化必然会损失信息，所以量化位数的设计对信息重建至关重要。量化位数越多，则信息损失越少，译码正确性越高，但计算量会增加、消耗的FPGA资源也越多；若量化位数太少，丢失的信息过多，虽然计算量减少、消耗FPGA资源减少，但可能造成译码错误。

　　文献[8-9]中提出(q，f)均匀量化方案，其中量化位数q=8，因量化精度对译码性能影响很小，故取f=2足矣。鉴于Xilinx XC7VX485T的逻辑资源相对丰富，本文设计了(8，2)、(9，2)、(10，2)、(11，2)4种量化方案，这4种量化方案经ISE布局布线后消耗FPGA中一种重要资源指标Slice Registers的情况如表1所示。

　　根据面积换“速度”的思想，提高FPGA资源利用率的同时增加译码的准确性。因此，根据表1可知(10，2)均匀量化方案最适合本文DSC译码量化要求。

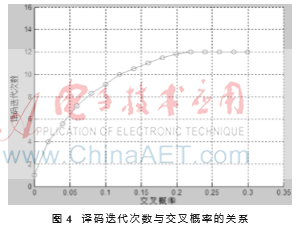
　　另一个重要的参数是译码迭代次数。通常码长、码率相同时，不同交叉概率对应的译码迭代次数不同。通过仿真AWGN信道下码长2 048、码率1/2、量化位数10 bits的信号，得出交叉概率与译码迭代次数之间的关系，如图4所示。

　　图4表明，交叉概率变大时，译码迭代次数随之增加。当交叉概率超过0.2后，译码迭代次数不再改变。所以本文设计译码迭代次数的最大值为12。

　　2.2 变量更新单元设计

　　从式（3）和式（4）可知，变量节点的更新主要是加法运算。初始信息与校验信息送入VNU更新变量节点并计算出各码位判决控制信息。其原理框图如图5所示，由于H矩阵非规则，所以设计了两种校验信息组合方式。

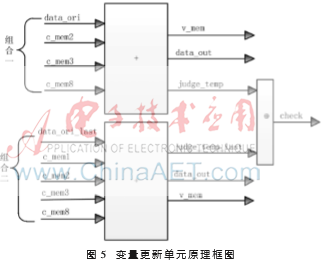
　　其中，data_ori、data_ori_last表示两种组合状态的初始信息，c_mem1、c_mem2、c_mem3、c_mem8表示分别与度为1、2、3、8的变量节点相连的校验节点信息，v_mem表示更新后的变量节点信息，judge_temp、judge_temp_last表示两种组合状态的中间判决信息，check表示输入判决模块的最终判决信息。

　　VNU计算完成后，将judge_temp、judge_temp_last进行异或运算得到判决结果check，如果判断结果是0，则表示译码正确，将译码结果送至串/并转换模块输出，否则表示译码错误。

　　2.3 校验更新单元设计

　　根据式(2)可知，更新校验节点信息需要求绝对值、求符号、排序找出最小值、移位和加运算这4个步骤。在式(2)中，虽然选择合适的η可以将乘法全部转化成移位和加法运算，但是大量的移位操作会占用过多的时钟周期，因此在CNU模块的移位/加运算中采用“流水移位/加运算”的方式，这样不但提高了时钟利用率、运算效率，也降低了FPGA资源的消耗。

　　CNU的原理框图如图6所示，由于H矩阵非规则，所以设计了两种变量信息组合方式。

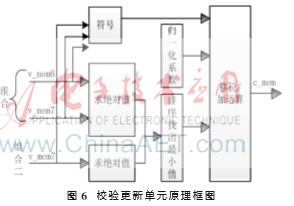
　　其中，v_mem6、v_mem7分别表示与度为6、7的校验节点相连的变量节点信息， c_mem表示更新后的校验节点信息。

3 DSC译码器设计结果分析

　　3.1 DSC译码器结构分析

　　通常情况下，串行译码的译码效率最低，全并行译码器的译码效率最高，但是FPGA有限的逻辑资源限制了这种方法的实用性。为了平衡FPGA资源的利用率和译码器的译码效率，本文采用部分并行的思想设计译码器。

　　由于本文的H矩阵是非规则的，不同度的节点组合在一起消耗的FPGA资源不一样。综合考虑运算量、FPGA资源、占用时钟周期等因素，设计VNU中组合一、组合二的结构如表2、表3所示。

　　从表2、表3中可以看出组合一的并行度是77，组合二的并行度是46。所以VNU组合一经过26个状态以及VNU组合二经过1个状态可以完全更新变量节点。

　　设计CNU中组合一、组合二的结构如表4、表5所示。从表4、表5中可以看出组合一的并行度是36，组合二的并行度是38，所以CNU组合一经过1个状态以及CNU组合二经过26个状态可以完全更新校验节点。

　　3.2 DSC译码器时序图

　　为了验证该DSC译码器设计的可行性，在MATLAB中随机产生一段二进制信息序列，先进行LDPC编码，再进行AWGN信道加噪和BPSK调制，得到初始化信息，然后作10 bits均匀量化，将量化结果存入Block RAM中作为译码器输入。

　　该译码器正确译码一次的主要信号时序图如图7所示(为了清晰地显示信号，故将图中的信号名重写)。信号的含义如下：clk表示译码器的全局时钟，rst表示译码器的全局复位，out_flag表示译码输出标志，out_en表示译码输出使能，iter_counter表示译码迭代次数，check表示译码判决信号，data_out表示译码输出。图7(b)、图7(c)是图7(a)中a、b局部放大后的图。

　　从图7(b)可以看出该译码器经过10次循环迭代后，判决信息输出为0，说明译码器译码正确。对比MATLAB产生的二进制信息序列，表明译码输出结果与产生的二进制信息序列完全一致，至此证明了该译码器设计是正确的。

　　3.3 DSC系统压缩性能

　　一般而言，信源的交叉概率越大，正确译码所需的校验位个数越多。为验证本文设计的DSC系统的压缩性能，通过改变信源的交叉概率测试正确译码需要的校验位个数，并与MATLAB中设计的DSC系统对比。本文设计的DSC系统与MATLAB中设计的DSC系统压缩性能对比如图8所示。

　　从图8中可知，在FPGA和MATLAB实现的DSC系统中，正确译码所需的校验位个数都随交叉概率增加而增加。当交叉概率相同时，本文设计实现的DSC系统比MATLAB仿真的DSC系统需要更多的校验位才能正确译码，主要原因是受FPGA资源限制导致量化位数不够并且FPGA在布局布线时有延迟。

　　该DSC高速译码器在Xilinx XC7VX485T上实现，ISE完成布局布线消耗的FPGA资源如表6所示。

　　经过时序约束，译码器最大工作频率f可达195.048 MHz，译出一个码字需要169个时钟。根据吞吐率计算公式N×f/(k×T)，其中N是码长，f是时钟工作频率，k是最大译码迭代次数，T是译出一个码字的周期，则译码吞吐率可达197 Mb/s。

4 结束语

　　本文针对当前DSC译码器译码实时性差、译码效率低等因素设计了一种全新的、高速部分并行的DSC译码器，并在Xilinx XC7VX485T芯片上实现，在设计时最大限度平衡了FPGA资源、译码复杂度和译码效率。该DSC译码器的设计具有一般性、便于移植等特点，其高达197 Mb/s的吞吐率，使该DSC译码器具有较强的工程实用性。

　　参考文献

　　[1] 杨春玲，夏洪涛，张兴绍.基于LDPC的码率自适应分布式视频编码[J].中国图象图形学报，2010，15(12)：1707-1713.

　　[2] CHUNG S Y，FORNEY G D，RICHARDSON T J，et al.On the design of low-density parity-check codes with in 0.004 5 dB of the Shannon limit[J].Communications Letters，IEEE，2001，5(2)：58-60.

　　[3] 薛国栋.分布式信源编码理论与应用研究[D].北京：北京邮电大学，2009.

　　[4] WANG J，YANG S H.A novel log-BP decoding algorithm for LDPC codes[C].Software Engineering，2009.WCSE'09.WRI World Congress on.IEEE，2009，1：305-307.

　　[5] JIANG N，PENG K，SONG J，et al.High-throughput QCLDPC decoders[J].Broadcasting，IEEE Transactions on，2009，55(2)：251-259.

　　[6] 姜博宇，姚远程，秦明伟.硬件可实现的LDPC译码算法研究[J].现代电子技术，2014，37(17)：5-8.

　　[7] COLE C.Error floor analysis for an ensemble of easily implementable irregular(2048，1024) LDPC codes[C].Military Communications Conference，2008.MILCOM 2008.IEEE.IEEE，2008：1-5.

　　[8] 刘文焘，李强，李少谦.π—旋转LDPC码译码算法及其量化研究[J].信息技术，2006，29(11)：38-40.

　　[9] 吴斌，杨波，叶明.LDPC硬件实现中的数据量化位数选择及其性能仿真[J].信息通信，2012(2)：24-26.