0 引言

    作为未来智能交通系统，车载网络VANET(Vehicular Ad Hoc Network)受到广泛关注^[1-4]。然而V2V(Vehicle to Vehicle)通信的连通率高度依赖于道路上的车辆密度。在低密度场景下，V2V通信的连通率低，由于车辆采用专用短距离通信DSRC协议^[5]，路由路径断裂率高。此外，V2V通信连通还受高速场景和城市场景的障碍物的影响，包括大的建筑物、大卡车等物体均会引起信号衰落^[6]。因此，面向V2V通信环境，分析车间连通对消息传输性能的影响是非常重要的。

    目前，针对VANET连通率低的问题，广泛采用基于存储-携带-转发SCF（Store-Carry-Forward）路由去桥接(bridging)的V2V通信的间隙(Gap)^[7]。车载容迟网络VDTN(Vehicular Delay-Tolerant Network)常采用SCF策略向目的节点转发数据包^[8]。现有的分析模型仅关注桥接一个通信间隙Gap^[9-10]，并没有考虑到多个间隙。对桥接多个间隙的累加时延和操作SCF的次数并没有进行理论分析。

    为此，本文针对多个V2V通信间隙Gap情况，建立基于存储携带转发路由的车间通信间隙时延分析模型 (SCF-GAM)，并评估SCF的端到端传输时延。同时，分析车流密度和车辆传输半径对传输时延和SCF操作的平均次数的影响，通过仿真数据验证了提出的模型的性能。

1 约束条件及问题描述

    假定所有车辆均基于DSRC进行V2V通信，它们也安装了全球定位系统GPS(Global Positioning System)，使车辆知道自己的位置、速度以及车间距离信息，传输半径均为R。

    考虑一维的VANET道路模型，如图1所示。双向单车辆，分别向东、西行驶。假定V₀和V_n+1分别表示数据源节点和目的节点，从V₀到V_n+1的路由距离为L。同时，假定在V₀到V_n+1的路由阶段中有k个车辆参与路由，表示为V_k(1≤k≤n)。用一维坐标位置表示沿途车辆V₀，V₁，…，V_n+1的位置。

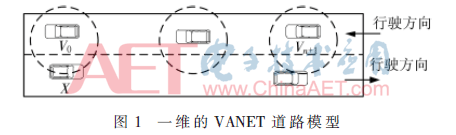
    假定第i个车辆V_i离车辆V₀的距离表示x_i。为了简化描述，假定V₀位于x₀=0。车辆通过周期地广播beacon消息，获取网络拓扑信息，每个beacon消息包含车辆的ID、位置x_i以及速度θ_i^[9]。

    数据从V₀至V_n+1的传输，多个车辆参与了路由。一旦检测到通信间隙Gap，如图2所示，V_k和V_k+1间未连通，此时利用反向车道的移动车辆X实施SCF策略去桥接通信间隙^[5]。因此，车辆V_k选择X作为中间转发节点，即数据从V_k→X→V_k+1，其中车辆V_k和V_k+1的速度分别表示为θ_k和θ_k+1。

2 分析模型

2.1 N_gap的概率质量函数

    为便于数学处理，假定两车辆间的空间服从指数的车头间距分布，且均值为1/μ^[10]。然后，沿着路由路径的总的车辆数服从泊松分布，其概率质量函数为：

    依据文献[11]，假定每辆车的位置在(0，s)区域均匀分布。基于将经典阶次统计学问题看成随机区间划分的理论[12]，在路由路径s存在m个通信间隙的条件概率：

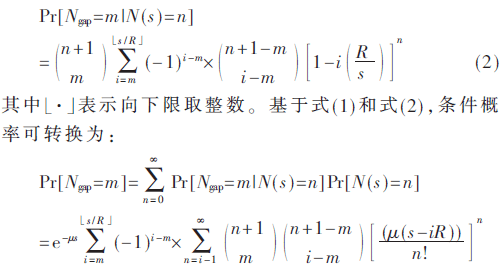
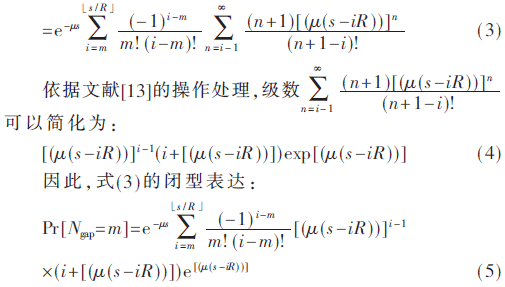
    依据式(5)便可计算在路由路径s上总的SCF操作数N_gap。接下来分析在桥接通信间隙所移动距离的拉氏变换，简称距离拉氏变换。

2.2 距离拉氏变换

    假定移动车辆X为桥接通信间隙所移动的距离为τ_g。如图2所示，V_k和V_k+1间的距离为d_k。如果d_k>R，两辆车间的通信不连通。SCF转发节点X与V_k+1间的距离表示为两个随机变量之和，即r₁+r₂。由于X在它们彼此通信范围内，移动距离τ_g等于r₁+r₂-R与0之间的最大值，即：

2.3 基于多通信间隙的SCF路由

    而桥接m个通信间隙所产生的总时延t_d如式(15)所示。式(5)～式(15)分析了具有多个通信间隙的路由路径的性能。基于这些分析，车载应用能预测路由时延，并且依据不同的服务要求，能自适应地调整参数。

3 性能分析

    为了验证模型的有效性，下面进行系统仿真。选择双向单车道的公路道路路段作为仿真模型。在每轮仿真过程中，采用一分为二的车头时距分布(Dichotomized Headway Distribution)，为束车辆(bunched vehicles)和单独车辆(Free vehicles)产生车间空间分布^[14]。依据文献[14]定义束车辆和单独车辆。对于束车辆而言，它与前一个车辆的车头间距小于Δ_th，而单独车辆表示它与前一个车辆的车头间距大于Δ_th。仿真过程中，Δ_th＝10 m。

    利用NS2仿真软件建立仿真平台，并利用SUMO产生车辆移动轨迹文件。采用Nakagami无线传播模型，车辆速度服从在[18，22]m/s区域均匀分布，仿真时间为300 s，每次实验独立重复50次，取平均值作为最终的仿真数据，将本文提出的分析模型得到的数据与仿真数据进行比较，将前者表示为Analytical，后者表示为Simulat。

3.1 车流密度μ的影响

    首先分析车流密度μ对SCF操作的平均次数和端到端传输时延的影响。车流密度μ从1～10 Veh/km，属于低密度情况。车辆传输半径为R=100 m，仿真结果如图3、图4所示。

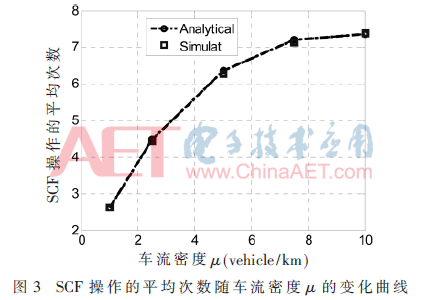
    从图3可知，SCF操作的平均次数随着车流密度μ的增加而增加，不过增加速度随之变缓。原因在于：μ在1～10 Veh/km间属低密度区域。换而言之，即使μ增加至10 Veh/km，仍属低密度区域。低密度区域意味着在该区域内车辆的通信连接存在问题。因此在μ从1～10 Veh/km的变化区间内，尽管密度的增加，可以改善通信连接问题，但是总体上仍有多数车辆间的通信无法建立，就需要更多SCF操作解决此问题。将Analytical与Simulat比较发现，两者差异很小，在车流密度μ从1变化至10 Veh/km区间，差异未超过2%。

    图4描绘端到端传输时延随车流密度μ的变化曲线。从图4可知，随着车流密度μ的增加，端到端传输时延下降。原因在于：车流密度μ的增加，SCF转发节点X向V_k+1转发消息所经历的路径更短，进而缩短了时延。此外，Simulat与Analytical两者差异不大。在μ=5时，差异仅为2.91%。

3.2 传输半径的影响

    本小节分析车辆传输半径端到端传输时延的影响。车辆传输半径R从50变化至500 m，车流密度μ分别为2.5、7.5、25 Veh/km。仿真结果如图5所示。

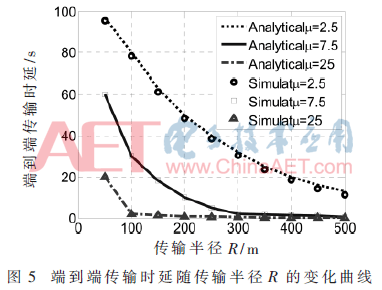
    图5分析了传输半径R对端到端传输时延的影响。从图5可知，端到端传输时延随传输半径R增加而下降，原因在于：传输半径R越大，车间通信跳数越少，时延就越短。而车流密度μ的越高，时延也越短。这主要是因为：车流密度μ的增加，减少了车间通信间隙Gap，降低了时延。此外，μ=2.5 Veh/km时，Simulat与Analytical两者的数据差异约在10%。

4 总结

    针对VANET中的车间通信间隙问题，本文提出基于存储-携带转发路由的车间通信间隙时延分析模型SCF-GAM。SCF-GAM模型分析并量化了通过移动车辆桥接通信间隙的时延以及SCF操作的平均次数。同时，通过仿真数据验证了SCF-GAM模型的准确性。

参考文献

[1] GORRIERI A，FERRARI G.Irresponsible AODV routing[J].Vehicular Communications，2015，3(2)：47-57.

[2] LIU J，JIANG X，MEMBER S.Throughput capacity of MANETs with power control and packet redundancy[J].IEEE Trans.Wirel.Commun.，2012，12(6)：3036-3047.

[3] RAK J.Providing differentiated levels of service availability in VANET communications[J].IEEE Commun.Lett.，2013，17(7)：1380-1383.

[4] LEE Y，TSAI M H，SOU S I.Performance of decode-and-forward cooperative communications with multiple dual-hop relays over Nakagami-m fading channels[J].IEEE Trans.Wireless Commun.，2009，8(6)：2853-2859.

[5] DARAGHMI Y A，YI C W，STOJMENOVIC I.Forwarding methods in data dissemination and routing protocols for vehicular ad hoc networks[J].IEEE Netw.，2013，27(6)：74-79.

[6] ISENTO J N G，RODRIGUES J J P C，DIAS J A F F，et al.Vehicular delay-tolerant network? A novel solution for vehicular communications[J].IEEE Intell.Transp.Syst.Mag.，2013，5(4)：10-19.

[7] SOU S I，TONGUZ O K.Enhancing VANET connectivity through roadside units on highways[J].IEEE Trans.Veh.Technol.，2011，60(8)：3586-3602.

[8] KESTING A，TREIBER M，HELBING D.Connectivity statistics of store-and-forward intervehicle communication[J].IEEE Trans.Intell.Transp.Syst.，2010，11(1)：172-181.

[9] VINEL A，CAMPOLO C，PETIT J，et al.Trustworthy broad-casting in IEEE 802.11p/WAVE vehicular networks：Delay analysis[J].IEEE Commun.Lett.，2011，5(9)：1010-1012.

[10] MCLEAN J R.Two-lane highway traffic operations：theory and practice[M].New York，USA：Gordon and Breach，1989.

[11] GALLAGER R G.Discrete stochastic processes[M].MA，USA：Kluwer，1999.

[12] DAVID H A，NAGARAJA H N.Order statistics[M].NJ，USA：Wiley，2003.

[13] SOU S I.A power-saving model for roadside unit deployment in vehicular networks[J].IEEE Commun.Lett.，2010，14(7)：623-625.

[14] SULLIVAN D P，TROUTBECK R J.An exponential relationship for the proportion of free vehicles on arterial roads[J].Transp.Res.A，Policy Pract.，1997，31(1)：21-33.