史文进，张兢，李冠迪,曾建梅

　　（重庆理工大学 电子信息与自动化学院，重庆 400054）

       摘要：节点定位是无线传感网络的关键技术之一，已经在军用、民用方面得到很广泛的应用。探讨了国内外无线传感网络定位技术现状，对无线传感网络节点定位技术做了调查研究，从锚节点/无锚节点定位、集中式/分布式定位、测距/非测距定位算法进行阐述，同时对各类算法从节点定位的定位精度、规模、功耗等不同角度进行了对比。重点探讨基于RSSI的质心定位算法，并进行仿真，结果表明其定位精度明显提高。

　　关键词：无线传感器网络；节点定位；测距/非测距

0引言

　　 重庆市教委科学技术研究项目(KJ1500917) 无线传感器网络(Wireless Senor Network, WSN)是由大量具有数据获取能力、无线通信传输数据能力、数据处理能力的微型传感器节点构成的网络［1］。在被监测区域放置成千上万的微型传感器节点，节点之间相互通信，形成一个以无线连接传输方式的网络。借助节点之间协作感知或者监视外部变化，对采集的信息进行预处理，同时通过基站将数据发送给用户。

　　WSN利用其信息获取和处理技术，在目标侦查跟踪、目标监测定位等相关领域有广泛应用。例如军事侦查、生态环境监测、目标定位、目标跟踪、特殊病人的监护与救护、幼童位置监测与救护等。无线传感器网络的目标位置识别、跟踪或目标定位是指通过分布区域内节点的物理坐标建立一个类似于GPS卫星定位无线传感器网络地图［2］。

1定位技术

　　在WSN中，节点向周围邻居节点发送信息，必须确定自身节点位置。由于网络中节点分布多、规模大，使得通过中心基站查询节点位置，无法短时间内完成。WSN中传感器节点硬件配置较低，传统的GPS因用户成本较高并不适合于WSN定位应用［3］。因此，节点在发送信息的数据中需包含自身的坐标信息。另外WSN中节点定位涉及到定位精度、节点规模、容错性和鲁棒性、能耗等。平衡定位精度是无线传感器网络定位的关键［4］。对于定位技术有很多种，本文从锚节点/无锚节点、集中式/分布式、测距/非测距几方面进行阐述。

　　1.1锚节点算法/无锚节点算法

　　锚节点定位方式是以锚节点作为参考节点。首先估计未知节点与锚节点的距离以及选择不同要求的算子进行未知节点的坐标初始化估计，最后对初始的未知节点的位置进行优化处理。锚节点的密度越高，参考节点越多，定位就越精确。但是由于增加了节点的数量，会导致系统成本增加。

　　无锚节点算法需要创建映射，通过节点间的映射关系估计测量节点间的距离。不同的映射关系，也会有不同的精度。有时是通过旋转、翻转、平移等创建映射关系。NISSanka［5］等人提出的算法是一种无需锚节点的定位，它是通过多跳确立一个映射关系，得到每个节点在坐标系中的坐标，最后采用质量—弹簧模型进行迭代优化。

　　1.2集中式算法与分布式算法

　　集中式定位算法：定位信息传送到一个中心基站，然后进行定位计算。集中式计算从全局出发，计算量和存储量几乎没有限制，实现实时定位。由于只有一个基站来完成计算，所以导致通信、存储消耗较大，最终导致电能消耗完，从而无法实现长时间的实时定位。

　　分布式定位算法：与集中式定位算法对应的一种算法，利用节点间的通信节点自行计算、估计节点位置坐标。集中式与分布式定位算法的对比如表1所示。

　　1.3测距/非测距定位

　　1.3.1基于测距技术的定位算法

　　这类定位算法是通过测量节点之间的距离或者角度进行定位。通过传感器来估计节点间的距离。常见的基于测距技术的定位算法有基于接收信号强度的算法(Received Signal Strength Indicator, RSSI)、基于信号到达时间的方法(Time of Arrival, TOA)、基于信号到达角的方法(Angle of Arrival, AOA)、基于信号传输时间差的方法(Time Difference of Arrival, TDOA)。

　　（1）接收信号强度算法(RSSI)：该方法依据接收信号能量强度(RSSI)确定距离，对通信信道参数要求较高。根据已知信号的发射功率和节点接收的信号功率，就可以测得节点间的距离。节点A到B的信号强度具体公式如下：

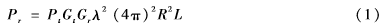
　　其中Pr是节点B接收信号强度，Pt是发射功率，Gt、Gr分别是A、B的天线增益，λ是波长，R是距离，L是损耗因子。由于信号传播的过程中，受到距离和障碍物的影响，信号的功率强度随之衰减，间接影响精度。所以对于短距离通信可以得到良好的精度。

　　（2）基于信号到达时间的方法(TOA)：TOA 也称为TOF(Time of Flight)。这种方法的前提是节点之间的时钟同步，移动终端发射测量信号到达基站，并施以特定算法的计算,就可以实现对移动终端的定位。其中距离可以通过下面的公式计算：

　　其中d是节点之间距离，c是传播速度，Δt为时间间隔。

　　（3）基于信号到达角的方法(AOA)：AOA指测量发送端和接收端的角度获得节点的位置信息最终完成定位。测量角度是通过安装在节点上的天线阵列，选择合适的三角测量术算法得到的。由于AOA方法需要在接收和发送两端安装天线阵列，其成本和能耗问题就会相应提高，所以AOA的实用性较差。

　　（4）基于信号传输时间差的方法(TDOA)：TDOA方法测量距离是根据两波到达同一目标或者不同目标的时间间隔。节点的距离公式如下:

　　其中d是节点之间的距离，Δt是接收时间间隔，S=(C1×C2)/(C1－C2)，C1和C2是两种波的传播速度。

　　对于不同的测距方式，定位算法需要根据精度要求进行选择，如表2是不同测距定位算法精度比较。

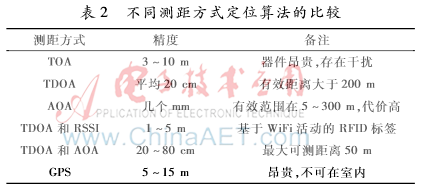
　　1.3.2无需测距技术的算法

　　此类算法不需要根据节点之间的通信距离进行定位，由于信息可以通过多跳方式发送，利用对跳数信息的处理估计两个节点间的通信距离，再根据算法得到未知节点的坐标位置。该算法无需测距，其优点是功耗低、成本低，缺点是定位精度不高。常见的方法有DVHop［6］和质心定位(Centroid Location, CL)。

　　（1）DVHop：DVHop算法是一种基于距离矢量计算跳数的算法。DVHop算法一般分为三个步骤：（1）计算节点之间的最小跳数；（2）每个锚节点计算自己的平均跳距；（3）通过三边法、极大似然法、最小二乘法［7］等估计未知节点的坐标。

　　（2）质心算法(CL)：质心算法基于网络的连通性，以未知节点周围的锚节点作为几何质心，每一个周期向邻边节点发送锚节点的坐标信息，最终未知节点确定为组成多边形的相对几何质心，以此估计未知节点的位置。设与未知节点联通的锚节点的坐标为(x1,y1)(x2,y2)…(xn,yn)，则由n个锚节点组成的n-1边的多边形质心(x,y)为：

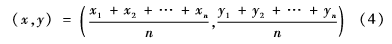
　　该质心定位算法相比于加权质心算法和三边测量法［8］较为简单，但位置错误率高。

2基于RSSI的质心定位算法

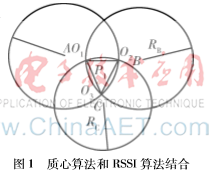
　　传统的质心定位算法简单，可行性高，但定位精度不高，常常定位不到目标。为了提高定位精度，提出基于RSSI的质心定位算法，使质心算法与RSSI相结合，通过RSSI的信号强度转化为传输距离，就可以提高定位精度。即邻居节点接收到信息后，记录锚节点的RSSI值，计算以锚节点为圆心的传输距离，记录下以传输距离为半径的所有圆的相交节点。对交点采用质心算法，就可以估计未知节点坐标。如图1所示，A、B、C为锚节点,未知节点P1必然落在三角形O1O2O3中。进一步对此算法进行仿真验证。

3仿真验证

　　实验环境使用MATLAB2010b版本仿真软件，在100 m×100 m的区域，30个未知节点随机分布，取平均误差值，比较质心定位算法、RSSI定位算法、基于RSSI质心定位算法的误差。仿真结果如图2

       图2中，实点是锚节点，星号是未知节点，圆圈是算法估计位置，连线是定位误差。结果表明质心算法和RSSI定位算法对未知节点的位置估计特性一般，而基于RSSI质心定位算法对未知节点的定位效果明显提高。

　　改变通信半径，在不同通信半径下的基于RSSI质心与质心定位算法误差比较，仿真结果如图3所示。

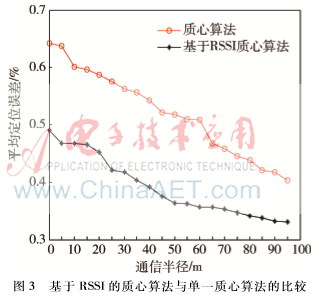
　　仿真结果表明，基于RSSI质心定位优化算法要比普通质心定位算法误差小，随着通信距离的增大，定位误差逐步减少，并在通信半径达到一定值后趋于误差平稳。如果未知移动节点越靠近参考节点，锚节点越多，则结果误差就越小。

4结论

　　随着定位技术的发展，廉价无线定位服务大众化趋势加剧。对基于RSSI的质心定位算法进行仿真表明，其定位精度比传统的质心算法的精度高，且具有低成本、设备少、距离远、易获取的特点。该算法基本满足高精度的定位需求，适用于定位精度、发射效率相对较高的无线定位系统。目前，许多算法只适合特定环境或需要对条件严格限定，且还有很多问题没有解决，如耗能、网络安全、测距干扰、定位优化、三维定位问题等，所以根据不同定位需求以及定位环境选择合适的定位算法很有必要。

　　参考文献

　　［1］ 邱岩, 赵冲冲, 戴桂兰. 无线传感器网络节点定位技术研究［J］. 计算机科学, 2008, 35(5): 47-50.

　　［2］ KOTWAL S B, VERMA S, ABROL R K. Approaches of self localization in wireless sensor networks and directions in 3D［J］. International Journal of Computer Applications, 2012, 50(11):1-10.

　　［3］ YAN L Q,GIANNAKIS G B. Ultra wide band communications an idea whose time has come ［J］. IEEE Signal Processing Magazine, 2005, 21(6):26-54.

　　［4］ 彭保.无线传感器网络移动节点定位及安全定位技术研究［D］.哈尔滨:哈尔滨工业大学,2009.

　　［5］ PRIYANTHA N B, BALAKRISHNAN H, DEMAINE E, et al. Anchorfree distributed localization in sensor networks［C］.Proceedings of the 1st International Conference on Embedded Networked Sensor Systems. ACM, 2003: 340-341.

　　［6］ 涂巧铃,牟小燕,宋佳. 一种改进的DVHop改进算法［J］. 重庆理工大学学报(自然科学),2014，28(11):84-88.

　　［7］ 孙利民.无线传感器网络［M］．北京:清华大学出版社,2005.

　　［8］ 徐林,傅成华.基于Zigbee的三边测量算法误差研究及改进［J］.微型机与应用,2012，31(21)：68-70.