满蔚仕,冯亚平,张志禹
(西安理工大学 自动化与信息工程学院 ,陕西 西安710048)
摘要:提出了一种故障分支判别的新判据和故障测距的新方法。故障分支判别充分利用双端行波定位原理和三端行波量测数据,考虑了测距误差因素对分支误判情况的影响,确保分支判别的有效性;故障点的测距通过对三端故障电压行波进行TT变换,然后提取信号TT变换模矩阵的对角线元素序列,利用TT变换对角线元素的频谱特性,精确标定行波波头到达量测点的时刻。MATLAB仿真结果表明,该方法正确可行,具有较高的测距精度,且在较大的环境干扰下可以实现T型线路的分支判别和故障测距。
关键词:T型线路;行波;故障测距;TT变换
0引言
输电线路故障测距一直是电力系统的研究热点。随着电力系统的不断发展,T型输电线路因其输送功率大等特点在高压输电线路中的应用变得越来越广泛。对T型线路故障测距算法的研究也越来越受到关注。T 型线路的故障测距主要分为两大类:故障分析法和行波法。故障分析法易受过渡电阻等因素的影响,测距精度不高,因此行波法是目前研究的热点。
目前,国内外学者针对T型线路行波测距已经提出了多种故障定位方法[12]。文献[2]和文献[3]首先利用双端行波原理进行故障分支判别,然后进行精确的故障测距。文献[4]利用现有的两端测距公式推导出了三端测距公式,在故障点的测距过程中消除了波速对测距结果的影响。文献[3]消除了波速对定位结果的影响,但需要通过波速来判断故障分支。
TT变换是近年来出现的一种时时分析方法。TT变换源于S变换,S变换是短时傅里叶变换和连续小波变换的延伸。TT变换[5]在2003年由PINNEGAR C R等人首先提出,是一维时间序列的二维实时表示,具有很强的局部时间分析能力,目前TT变换在电能质量检测中取得了良好的效果,应用于故障诊断分析则较少。
本文提出了T型线路故障分支判别的新判据和故障测距的新方法。先通过三端量测数据对T型线路进行故障分支判别,再对相模变换后的故障电压行波进行TT变换,得到TT模矩阵,检测TT模矩阵对角线元素的幅值突变点即行波首波头到达量测点的精准时刻。该方法只需获取行波首波头的到达时刻,不需考虑行波折反射,能在T节点附近发生故障时正确判别故障分支并进行精确的故障测距。
1故障分支判别及测距

如图1所示,以PT段发生单相短路故障为例说明分支的判别方法。当M点发生单相接地短路故障时,输电线路产生故障电压行波并以接近光速的速度向三端传播。
故障分支判别由以下公式计算:



式中,lij是两个量测端的线路长度,ti是行波到达量测端的时间,v是行波波速。故障分支的判据为:若dRT≤lRP且dRS≤lRP,则故障在RP支路;若dRS>lRP且dST<lSP,则故障在SP支路;若dRT>lRP且dST≥lSP,则故障在TP支路。
故障分支判别后进行测距。故障在RP支路时,dRM=dRT+dRS/2;故障在SP支路时,dSM=(lRS-dRS)+dST/2;故障在TP支路时,dTM=(lRT-dRT)+(lST-dST)/2。
2TT变换检测行波首波头到达时刻
2.1TT变换及其对角线元素分析
信号的S变换定义为:

S变换的窗函数定义为:
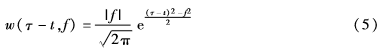
对S变换进行傅里叶逆变换,就得到TT变换:
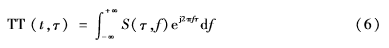
TT变换对角线元素定义为[6]:
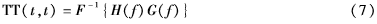
式中,F-1为傅里叶逆变换,H(f)为信号h(t)的傅里叶变换;G(f)由积分变换可得:

式中pk(1)是常量,k=tτ,p1(1)-0.021 99,p3(1)-0.006 79,p5(1)-0.004 05。
式(8)表明,G(f)与|f|成正比,|f|越大,G(f)越大,即对角线元素值越大,因此在t=τ时,信号的高频部分比低频部分的振幅更高。输电线路短路故障会产生高频分量,因而可用TT变换来精确定位行波首波头的到达时刻。
2.2故障行波首波头到达时刻检测
本文选取三端故障电压行波作为量测量。先截取故障前后三端母线的故障电压行波,然后利用Clark变换对其进行解耦,选取解耦后的α模电压分量进行故障测距研究。
当T型线路某处发生短路故障时,线路中将产生故障行波。对α模电压分量进行TT变换得到TT模矩阵,提取模矩阵对角线序列。对角线序列中模最大值对应的采样时刻即为故障电压行波首波头到达该量测点的时刻。
假设输电线路某处发生单相短路故障,故障电压经Clark变换后得到故障前后一段时间的α模电压波形,如图2所示。

由图2可知,α模分量出现大的波动,但不确定精确时间。对图2行波进行TT变换并提取TT变换对角线元素确定行波首波头的精确到达时刻。图3为对角线元素序列幅-时图。

由图3可见,模最大值对应的采样时刻为176个采样点处。因此,TT变换对角线元素序列中模最大值对应的时刻即为行波首波头的到达时刻。大量仿真结果证明,此方法能够精确检测行波首波头的到达时刻。
3仿真分析
为验证方法的有效性,对单回T型线路进行仿真。线路模型如图1。线路长度lRP、lSP、lTP分别为100 km、150 km、200 km。线路的正序和零序参数为r1=0.012 73 Ω/km,L1=0.933 7 mH/km,C1=0.012 74 μF/km;r0=0.386 4 Ω/km,L0=4.126 4 mH/km,C0=0.007 75 μF/km。系统3端电源E·R、E·S、E·T电动势为500 kV,初始相位角分别为0°、30°、60°。信号仿真的采样频率为1 MHz,根据线路参数,波速度v=289 950 km/s。
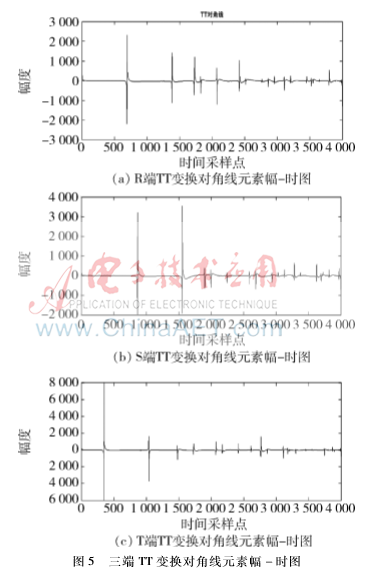
仿真算例1:线路TP区间距离T端100 km处,t=0.035 s时发生A相短路故障,接地电阻和过渡电阻均为50 Ω,考虑到实际运用,各电压信号均加入40 db的高斯白噪声。图4中(a)、(b)、(c)分别为R、S、T量测端测得的故障电压行波,经过TT变换如图5(a)、(b)、(c)。可测得行波首波头到达三端的采样时间分别为693、866、348个采样点,即tR=0.000 693 s、tS=0.000 866 s、tT=0.000 348 s,代入公式(1)、(2)、(3),可得dRS=99.919 3 km、dRT=225.097 1 km、dST=225.016 4 km。满足TP故障的判定条件,判定TP支路发生故障。由上述测距公式可得dTM=99.943 2 km,误差为56 m。

仿真算例2:P节点故障。假设RP支路距R端99.5 km处,t=0.035 s时发生A相短路故障,接地电阻为200 Ω,过渡电阻为50 Ω。同理可得行波首波头到达三端的时间分别为346、523、695采样点,即tR=0.000 346 s、tS=0.000 523 s、tT=0.000 695 s,代入公式(1)、(2)、(3),可得dRS=99.339 4 km、dRT=99.403 7 km、dST=150.064 3 km。满足RP分支故障的判定条件,判定RP支路发生故障。由上述测距公式可得dRM=99.371 6 km,误差为128 m。采用本方法克服了传统缺陷,在P节点附近0.5 km还能正确判别故障支路,确定故障位置,无测距死区,测距精度高。
表1列出了在加入40 db的高斯白噪声干扰下,发生各种故障时本文方法的测距结果。由表1可知,本文方法在T型线路各支路范围内都可以测距,测距精度很高。
表2列出了不同过渡电阻下本文的测距结果,设故障点在TP支路上。由表2可知,本文方法基本不受过渡电阻影响,当过渡电阻很大时,还能达到很高的测量精确度。


4结论
本文在行波测距基础上, 对T型线路的故障测距进行了研究, 提出了分支判别的新判据和故障测距的新方法,通过TT变换对角线元素序列的谱分析,精确捕捉行波波头到达量测端的时刻。并对T节点附近发生短路故障进行了研究,传统方法在T节点附近故障时无法正确判别故障分支,采用本文方法可以正确判别故障分支。MATLAB仿真结果表明本文方法的有效性,并且不受故障类型、故障距离和过渡电阻的影响,有一定的抗干扰能力,具有一定的实际应用价值。
参考文献
[1] 李传兵, 谭博学, 高鹏, 等.基于D型行波原理的T接线路故障测距方法[J]. 电力系统保护与控制, 2013, 41(18):78-82.
[2] 张峰,梁军,杜涛,等.T 型线路的行波精确故障测距新方法[J].高电压技术,2009,35(3):527-532.
[3] 郭亮, 吕飞鹏. T型线路的行波测距原理与算法[J].电力系统保护与控制, 2010, 38(23):6467, 74.
[4] 张永健, 胥杰, 孙嘉. 基于静态小波变换的T型输电线路行波测距方法[J]. 电网技术,2012, 36(6):84-88.
[5] PINNEGAR C R, MANSINHA L. A method of timetime analysis: the TTtransform[J]. Digital Signal Processing, 2003, 13(4): 588-603.
[6] STOCKWELL R G, MANSINHA L, LOWE R P. Location of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing,1996,44(4):998-1001.

