朱进勇,王立冬
(军械工程学院 电子与光学工程系,河北 石家庄 050003)
摘要:在无线电测向领域,相干信号对测向精度和分辨性能有着较大影响,如果将相干信号和多径信号之间的关系相互混淆,会产生较大的测向误差。首先建立了空地多径效应三径模型,对多径信号之间的关系和多径信号对测向的影响进行具体分析;采用相关性理论,对信号的相干性进行了详细分析,进而讨论了多径信号的相干性;最后,在SystemVue软件环境下对空地多径效应三径模型进行了仿真建模,由仿真结果得出了多径信号之间的相干规律及其对测向的影响规律。
关键词:相干信号;多径效应;测向;SystemVue软件
中图分类号:TN95 ;TN97文献标识码:ADOI:10.19358/j.issn.16747720.2016.20.004
引用格式:朱进勇,王立冬. 多径信号的相干性及对测向的影响[J].微型机与应用,2016,35(20):17 20,24.
0引言
在电磁波的传播过程中,由于自然环境的多变性和复杂性,导致进入接收机的信号中存在相干信号。相干信号的干扰分为同频干扰和多径干扰,同频干扰[1]是临近同频段的雷达所发射的信号进入接收机后产生的干扰;多径干扰是由于背景物体的反射造成信号的传播存在多种路径,在接收机处相互叠加而产生的干扰。相干信号源的存在会导致接收机的虚警或者目标的定位不准确,甚至出现错误。相干信号对DOA(Direction of Arrival)估计有着不利影响。例如,传统的超分辨测向算法[2] (MUSIC)对相干信号没有效果。文献[3]对信号的相关性进行了分析,并对相关信号和不相关信号进行了DoA估计的仿真,但是其仿真的条件比较理想化,没有基于实际测向环境进行分析,所以其结论应该只适用于频率和初始相位都相同的信号;文献[4]对反射路径电场强度的理论分析没有考虑反射时的能量损耗,所以其得到的角度偏差值也存在误差。
本文建立了空地多径效应三径模型,分析了多径信号对测向的影响,完善了文献[4]对反射路径场强的理论计算;采用相关性理论对信号的相干性进行了具体分析,讨论了多径效应与相干信号之间的关系;最后,在SystemVue[5]环境下,建立了完整的空地多径效应三径模型,分析了多径信号之间的相干性及其对测向的影响。
1多径效应对测向的影响及其相干性分析
多径效应[6]是指电磁波在传播过程中的多径传输现象所引起的干涉时延效应。
在实际的测向过程中,接近地面的接收设备不仅接收由信号源直接传输过来的直射信号,还可能接收到由周围环境如高山、丛林、建筑物等经过多路径反射后的干扰信号。由于直射信号与多径反射后的干扰信号频率相同,仅仅在相位和信号强弱上有所差别,因此,接收机测向系统很容易对这些信号产生误判,不能区分哪个信号是直射信号,哪个信号是反射后的干扰信号,造成测向不准确甚至无法得到目标方位角信息的现象。为此,本文建立了典型的三径模型,分析了多径信号对测向的影响及其相干性。
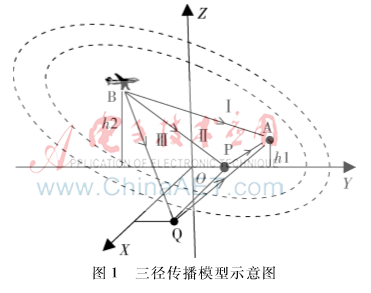
图1所示为空地三径模型。其中XOY平面为水平面,Z轴垂直于XOY平面向上。接收机A的高度h1,发射机B的高度为h2。为了便于分析,设直射传播路径BA(用Ⅰ代替)在XOY平面上的投影位于Y轴上,反射传播路径Ⅱ的反射点P也位于Y轴上,反射传播路径Ⅲ的反射点Q不在Y轴上,是任意的一条路径。因为路径Ⅱ在XOY平面上的投影位于Y轴上,所以它在接收天线处不影响对方位角的测量,但对俯仰角有较大的影响。路径Ⅲ对方位角和俯仰角的测量都有影响。图中的两个虚线椭圆是以A和B为焦点的信道椭圆模型[7],因此,所有位于同一个虚线椭圆上的反射点所产生的反射波具有相同的传播路径长度,也就是具有相同的时延。
根据自由空间无线电磁波的传播理论[7-8]可得,路径Ⅰ在接收天线处产生的场强为

式中, Pt(kw)为发射机天线的输入功率,G1为发射天线在直射路径方向的增益,d1为直射路径的距离(km)。
路径Ⅱ和路径Ⅲ在地面进行了二次反射,可以将反射点当作一个点辐射源来分析其产生的场强大小。其中,路径Ⅱ在反射点的场强为

根据平均功率流密度公式

得到反射点的反射功率为

所以,路径Ⅱ反射后经过d22的距离到达接收机处产生的场强为

式中, G21为发射机到反射点的增益,G22为反射点到接收机的增益,A1为地面对无线电磁波的反射率(草地上的反射率一般为0.4~0.6,金属表面的反射率一般为0.8~0.9),d21为发射机到反射点的距离,d22为反射点到接收机的距离,η为波阻抗(
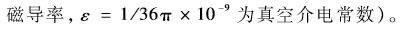
同理,可以得到路径Ⅲ在接收机处的场强为
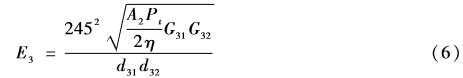
其中, G31为发射机到反射点的增益,G32为反射点到接收机的增益,A2为地面对无线电磁波的反射率,d31为发射机到反射点的距离,d32为反射点到接收机的距离。
由式(1)、(5)和(6)可得,在接收机处的总场强为
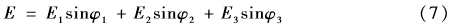
式中, φ1、φ2、φ3为各路径的场强方向与大地垂直线方向的夹角。发射机与接收机的水平距离为l,路径Ⅲ在X、Y轴上的投影距离为s和a。路径Ⅰ和路径Ⅱ的场强在XOY平面上投影为


路径Ⅲ在XOY平面上投影为


由图2中的三路径场强投影图可以看出,路径Ⅱ对路径Ⅰ方位角的测量没有影响,而路径Ⅲ使路径Ⅰ的方位角产生了偏移。因此,在方位角的角度偏移上只考虑路径Ⅲ对路径Ⅰ的影响。设偏移角度的弧度值为β,根据场强大小可以得到


实际测向过程中,容易产生多径信号,存在多径效应。由上述分析可得,多径效应对测向将产生较大影响。
2多径信号的相干性分析
设两个信号X1、X2的相关程度采用相关系数[9-10]ρ来衡量,其定义为



式中cov(X1,X2)为两个信号的协方差函数,E(X)为数学期望,μ(t)和D(X)分别为两信号的均值函数和方差函数。当ρ=0时,两信号不相关;当0<|ρ|<1时,两信号相关;当|ρ|=1时,两信号相干。设
 w1和w2为信号X1和X2的频率,φ1和φ2为两信号的初始相位,其相关系数表示为
w1和w2为信号X1和X2的频率,φ1和φ2为两信号的初始相位,其相关系数表示为
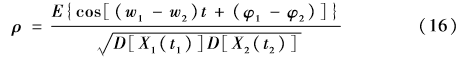
式中 恒大于0,由式(16)可得:
恒大于0,由式(16)可得:
(1)w1≠w2时, ρ=0,即两个频率不同的信号是不相关的;
(2)w1=w2时,若φ1=φ2以及两相位差180°,则|ρ|=1,两信号为相干信号;若两相位差为90°或270°,则ρ=0,两信号不相关;若两信号的相位差不属于以上两种特殊情况,0<|ρ|<1,则两信号相关,但不相干。
由第1节中多径信号的三径模型分析以及上述相关性理论分析可知,多径信号的频率相同,但是由于其相位关系的不同,它们可能是相干的,也可能是不相干的。多径信号中,当两信号的相位相同或者相位差为180°时,两信号为相干信号;当两信号的相位差为90°或270°时,两信号相互独立;当两信号的相位差不属于这两种情况时,两信号相关但不相干。
3多径效应的SystemVue仿真系统设计
利用SystemVue软件构建空地多径效应模型,可以定量仿真分析多径信号的相干性及其对测向的影响。空地多径效应三径模型测向系统由发射机系统、路径Ⅰ、路径Ⅱ、路径Ⅲ以及MUSIC算法处理部分组成。
为了深入分析该测向系统,将多径模型测向系统分为发射机系统和地面接收机系统,如图3和图4所示。


图3中,RADAR_LFM模块产生所需要的线性调频信号,信号形式PW为30 μs,脉冲重复频率PRI为104 Hz,带宽BW为5 MHz;该信号通过Set Sample Rate采样模块变为离散化的信号形式;该离散化的信号通过RADAR_Tx_DBS模块形成阵列信号的数字波束;该数字波束信号通过RADAR_MultiCH_Tx模块,实现多信道的发射;并通过RADAR_PhaseArrayTx模块,完成仿真发射电子扫描阵列[11](ESAs)。ESAs能够提供可控制的、角度化的、高增益的波束。与传统的反射面天线相比,ESAs能够在空间电子地扫描阵列波束,而不需要通过物理地移动阵列,其微秒级扫描波束在精度上远高于反射面天线的毫秒级扫描波束。
图4为路径Ⅰ的接收线路。从信号源到来的电磁波通过RADAR_PhaseShift模拟模块产生从远区电场到观测点的数字阵列天线的相移,即可以设置二维阵列天线中X轴8个阵元为Y轴1个阵元,阵元之间的间距为半波长,远区电场观测点与信号源之间的方位角设为20°;然后,RADAR_MultiCH_Rx模块对数字阵列天线的信号进行接收处理;最后,Commutator模块对接收后的8路信号进行整流处理,得到一路信号。
路径Ⅱ的接收路线与路径Ⅰ相类似,只是在RADAR_PhaseShift模块前面设置一个Delay模块和Gain模块。Delay模块参数设置为10,相当于延迟时间为1 μs,即电磁波经反射后路径Ⅱ相对于路径Ⅰ多传播了300 m;Gain模块的参数设置为0.005,相当于副瓣经过反射后的衰减(草地上的反射率为0.4~0.6);该路径中,RADAR_PhaseShift模块的角度设置与路径Ⅰ相同,相当于路径Ⅱ不影响直射路径的方位角测量。
路径Ⅲ与路径Ⅱ 类似,只需要作以下修改:将Delay模块的参数设置为20,相当于延迟时间为2 μs,即反射后的路径Ⅲ比路径Ⅰ多传播了600 m;方位角的角度设置为25°。
完成以上设置后,将3路信号送入Add模块整合为一路信号;将该信号送入Pack_M模块,实现8行1 024列的矩阵打包;最后,MathLang模块采用经典的MUSIC算法对矩阵包(三路信号)进行波达方向角估计,分析多径信号的相干性及其对测向的影响。
4仿真结果分析
在SystemVue软件仿真平台上运行上述多径模型测向系统,可得如图5~图10所示的仿真结果。
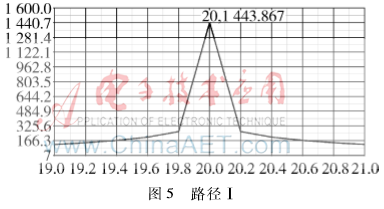
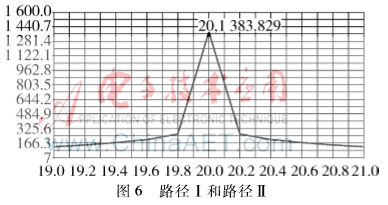
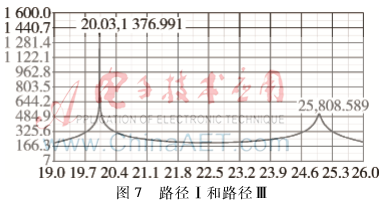
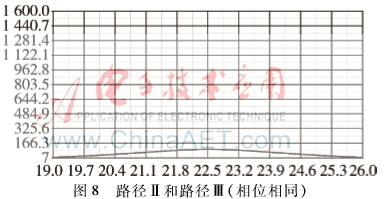


图5为路径Ⅰ的测向波形图,在该波形图可以看到只有一个尖峰;图6为路径Ⅰ和路径Ⅱ两条路径共同作用的波形图,该图中仍然只能见到一个尖峰;图7为路径Ⅰ和路径Ⅲ两条路径的波形图,该图中可见到两个尖峰。其中,第一个尖峰为路径Ⅰ产生的,第二个尖峰为路径Ⅲ产生的。相对于第一个尖峰,第二个尖峰较平缓,幅度值较小。由图5~图7得到的具体参数值如表1所示。由表1中的数据可以得出:
(1)路径Ⅰ和路径Ⅱ两条路径共同作用时的尖峰幅度值小于路径Ⅰ的幅度值。这说明多径信号进入接收机导致接收信号衰落。
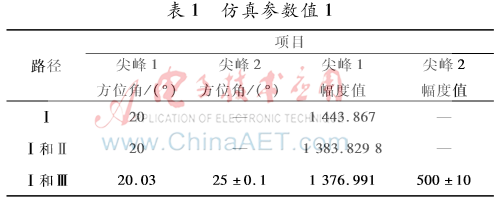
(2)路径Ⅰ和路径Ⅲ为同频不同相位,经典的MUSIC算法能够明显地将两路多径信号分辨开来。由于MUSIC算法对相干信号无效,因此路径Ⅰ和路径Ⅲ这两种同频不同相位的信号不是相干信号。这与前面的理论分析是一致的。
(3)图7中,路径Ⅰ所测得方位角为20.03°,与实际方位角度值20°有0.03°的差值,与上文理论分析中的β值乘以180/π(弧度转化为角度)后的角度偏差值是一个数量级,这是误差允许范围内的。
图8为路径Ⅱ和路径Ⅲ在相位相同情况下的波形图,在该图中完全不能见到任何峰值的点,整个波形平缓;图9为路径Ⅱ和路径Ⅲ在相位不相同情况下的波形图,在该图中能够见到路径Ⅱ和路径Ⅲ的两个峰值,但是幅度值较小;图10为 路径Ⅰ、路径Ⅱ和路径Ⅲ同频但不同相位的波形图,图中能够见到两个峰值,第一个峰值很尖锐,为路径Ⅰ和路径Ⅱ叠加以及路径Ⅲ对其测向的影响所产生的,第二个尖峰为路径Ⅲ所产生的,其幅度值相对第一个尖峰较小,其尖峰也相对平缓。由图8~图10得到的具体参数值如表2所示。

从表2中的数据可以看出:
(1)MUSIC算法不能够将路径Ⅱ和路径Ⅲ相位相同的信号分辨开来,而可以将相位不同的两信号分辨开来。这说明同频同相位的信号为相干信号,同频不同相位的信号为不相干信号;多径效应产生的相干信号对测向有着严重的影响,尤其是采用MUSIC算法,这类特征值分解类算法时,测向分辨效果很差。
(2)图10中,路径Ⅰ和路径Ⅱ共同作用的路径受到路径Ⅲ影响所得到的方位角度值为20.04°,与上文理论分析所得到的角度偏差值也是在一个数量级的,这是在误差允许范围内的。
5结论
本文建立了多径效应的三径模型,分析了多径信号对测向的影响,得到了测向误差理论公式;推导了多径信号相关性分析公式,对多径信号的相干性进行了理论分析;在SystemVue仿真环境下,采用空地多径效应三径模型,仿真分析了多径信号与相干信号之间的关系以及相干信号对测向的影响。由仿真结果可得,多径信号由于经历了反射环境的变化导致了接收信号的衰落;经过反射后的信号会对直射路径信号的测向产生影响;多径信号中的同频同相位信号是相干信号,而同频不同相位信号不是相干信号,且多径信号将严重影响特征值分解类算法的测向分辨效果。该规律对设计测向算法、提高测向精度具有一定的指导意义。
参考文献
[1] 毛滔,曾浩.雷达抗同频干扰方法研究[J].航天电子对抗,2005,21(6):43-45.
[2] SCHMIDT R. O. Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation, 1986,34(3):276-280.
[3] 熊波,李国林,尚雅玲,等.信号相关性与DOA估计[J].电子科技大学学报, 2007,36(5):907-910.
[4] 李博章,谢飞,刘坤.多径效应对测向方位角的影响分析[J].船舶电子工 程, 2010,30(2):81-83,110.
[5] DAVID L, ANURAG B. Radar system design and interference analysis using Agilent SystemVue [Z].Agilent Technologies Application Note,2010.
[6] 毛虎,杨建波,邱宏坤.多径效应对信号接收及方向测量的影响[J].电讯技术,2010,50(10):63-68.
[7] 封吉平,曾瑞,梁玉英.微波工程基础[M].北京:电子工业出版社,2002.
[8] 丁鹭飞,耿富录.雷达原理(第3版)[M].西安:西安电子科技大学出版社,1995.
[9] 张玉宪,魏少明.多径效应对无源定位性能的影响[J].电子测量技术,2009,32(7):18-21.
[10] 谢飞,张忠臣,张鹏,等.多径效应对测向误差的影响[J].电子测量技术,2010,33(1):29-31,39.
[11] 薛正辉,李伟明,任武.阵列天线分析与综合[M].北京:北京航空航天大学出版社,2011.

