张志禹,赵良辰,满蔚仕
(西安理工大学, 陕西 西安 710048)
摘要:S变换因其优良的时频特性而在故障定位方面获得了广泛的应用,但由于S变换计算时采用等间隔采样频率点,因而计算量较大,且存在运算速度和测距精度之间的矛盾,即为了提高测距精度必须提高采样频率,但提高采样频率就会降低算法的运算速度,降低了实时性。为此文章提出了一种自适应于测距信号的S变换,该算法针对信号的特定成分进行时频分析,在提高测距精度的基础上,减少了算法运算量,保证了系统的实时性。并对包含噪声情况下该方法的准确度进行了分析验证。实验结果证明,自适应S变换在保证系统实时性的前提下能够有效提高测距精度。
关键词:行波测距;自适应;采样频率;精度
中图分类号:TM 771文献标识码:ADOI: 10.19358/j.issn.16747720.2016.23.002
引用格式:张志禹,赵良辰,满蔚仕. 自适应S变换在故障测距的应用研究[J].微型机与应用,2016,35(23):9-11,14.
0引言
我国配电网中普遍采用小电流接地系统[1],单相接地故障发生后,由于小电流系统不构成短路回路,系统可在故障发生后继续运行1~2 h。因此,采用小电流接地方式对供电可靠性有显著作用。但在故障状态下长时间运行,出现的过电压(特别是弧光过电压),可能引起绝缘的薄弱环节被击穿,发展成为相间短路,使事故扩大,影响用户的正常用电。还可能使电压互感器铁心严重饱和,导致电压互感器严重过负荷而烧毁,威胁电网的安全运行[2]。因此,如何能够快速准确地定位单相接地故障发生位置,对于电力系统的稳定运行具有重要意义。
由于S变换优良的时频特性,利用S变换的行波测距法已经成为故障定位的主要方法。而利用S变换的故障定位,通常是利用S变换的模时频矩阵其中的某一频率下的幅值时间曲线,实际上其余频率点并未使用。由于S变换对所有频率点都要进行运算,当信号采样频率提高时,采样点数增加,S变换时间也大大增加,影响了故障测距的实时性。故本文提出了自适应S变换,只计算故障信号特定频率点下的S变换结果,大大减少了需要处理的数据量,节约了运算时间。
1采样频率对误差的影响
由D型行波测距法故障距离计算公式dmf=12(L+(tm-tn)v)可知,D型行波测距法误差为:

式中,L为线路总长度,fs为采样频率,d为实际故障距离,v为行波波速。
由上式可以得到D型行波测距法测距精度为v/2f。当采样频率为100 kHz时,设波速近似为光速3×108 m/s,测距精度为1.5 km。实际工程中,1.5 km的测距精度能够较好地满足远距离输电线路的故障测距需求,但对于短距离配电线路,则要求更高的测距精度。当采样频率提高时,测距精度也将提高,但同样的,S变换的计算量也将大幅度提高。对于低压配电线路,采样频率宜在10~20 MHz之间[3]。
当采样频率为100 kHz时,仿真时间设置为0.1 s,即采样点数为10 000个时,S变换计算的频率点为5 000个;而当采样频率提高到10 MHz时,采样点数为1.0×106个,所需计算的频率点数为5.0×105个,需要计算的数据量甚至已经超出了MATLAB的存储空间大小,计算时间过久,无法满足实时处理的需求。
因此,本文提出采用自适应S变换,简化运算过程,在提高测距精度的基础上,保证算法实时性。
2自适应S变换
2.1S变换基本原理
信号的S变换定义[4-7]如下:
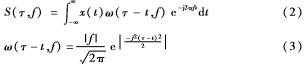
式中,ω(τ-t,f)为高斯窗口,f为频率,τ为控制高斯窗口关于时间轴t的位置参数。由式(2)可以看出,不同于短时傅氏变换,S 变换的高斯窗口宽度及高度随频率变化而变化,从而克服了短时傅氏变换窗口宽度、高度固定不变的缺陷。
通过S逆变换,可以由S(τ,f)很好地重构x(t),其逆变换公式如下:
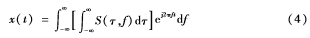
设信号x(kT),k=0,1,2,…,N-1是对连续时间信号x(t)采样得来的离散时间序列,T是采样间隔,N是采样点数。该序列的离散傅里叶变换为:

2.2自适应S变换原理
自适应S变换实际上是利用预先确定好的信号中的有效频率成分作为S变换的输入,代替了S变换原本遍历性的频域迭代计算方式。对于应用了S变换的行波测距法来说,通常是首先从S变换模时频矩阵中提取特征向量,然后再利用这些参数进行波头识别以及故障定位。其中所提取的特征向量一般是S模时频矩阵特定频率下的时间幅值分量。因此如果能只针对特定频率点进行S变换,就可以大大减少工作量。其离散形式[8-9]的表达式为:
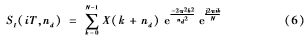
式中,nd为用来识别行波波头的时间幅值分量所处的频率点。其确定的主要依据是S变换后能清楚识别故障行波波头,使其不被噪声淹没。自适应S变换计算流程如下:
(1)利用FFT计算故障行波信号的离散傅里叶变换X(k);
(2)确定X(k)的频率点nd;
(3)计算对应于频率点nd的高斯窗函数G(nd,k);
(4)将X(k)移位至X(k+nd),对X(k+nd)进行加窗处理,也就是将X(k+nd)、G(nd,k)相乘,得到X(nd,k);
(5)求B(nd,k)反傅里叶变换,得到对应于频率点nd的S变换结果。
由于频率点的选择方法,当噪声大小以及故障点过渡电阻等条件发生改变时,可能无法得到可以清楚识别波头的时间幅值曲线。因此本文提出一种采用自适应的办法解决该问题,确定自适应S变换频率点。
主要原理是一个循环过程。实验发现,相差1 kHz以下的频率点,分别进行行波测距,所得到的测距结果几乎相同。因此本文以最高频率的40%频率点为基准,以1 kHz为步长,当所选的频率点S变换结果,行波波头被噪声淹没而无法识别波头时,降低所选频率,再次进行S变换,直至可以识别出行波波头为止;当S变换结果能够识别波头时,判定波头幅值是否高于噪声平均幅值的50%。当波头幅值高于噪声平均幅值50%时,可以认为波头能够被清楚地识别,如果不高于,则应提高频率,直至能够清楚地识别行波波头。该算法经过3~4个频率点的S变换即可得到最优的频率点,与传统S变换需要在106个频率点处进行S变换相比,计算量大大减少。
该方法流程图如图1。

3自适应S变换的模型仿真验证
模型参数为:线路电压等级为110 kV,频率50 Hz。采样频率为10 MHz,仿真时长为0.1 s。线路全长132 km,故障点距离N端25 km。
线路结构参数为:

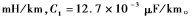
将实际线路参数代入波速计算公式 可以计算得到波速约为2.981 13×105 km/s。
可以计算得到波速约为2.981 13×105 km/s。
故障于0.035 s发生,M端监测点测得的三相电压如图2所示,可以看出故障发生后,故障相相电压明显降低。

经Clarke变换后,得到的α模分量如图3。

由图3可以看出,波形共包括1 000 000个采样点,如进行完全S变换,则需在500 000个频率点处进行S变换,计算量巨大,运算时间过长。由于高斯白噪声的存在,如果选取过高频率分量进行行波测距将导致信噪比过低,噪声影响加剧,无法识别行波波头;如果频率分量选取过低,则由于S变换窗函数宽度较宽,无法准确地获得初始行波波头达到时刻,导致最终测距结果误差变大,准确率下降。因此,在S变换结果最高频率为5 MHz的情况下,选取自适应S变换的频率点为2 MHz。得到的S变换结果如图4。

由图4可以看出,选择初始频率点即可准确定位故障点,波头到达的时刻分别为352 854、350 841。根据双端行波测距公式,取行波波速为计算波速2.981 13×105 km/s,最终测距结果为24.995 km,误差5 m。
但当系统所含噪声增大时,选择初始频率点未必就能准确定位故障位置。图5为系统噪声为70 dBW时,S变换结果中2 MHz频率分量。

其中,M端观测到的最大值为2 817,出现在721 762时刻处。此时M端无法观测到明显的波头,最大值均未高出噪声平均幅值50%。
因此,以1 kHz为步长,减小所选频率。当选择频率为1.5 MHz时,所得分量如图6。

M、N两端,均可观测到明显的波头,所得波头到达时刻分别为352 853、350 841。根据双端行波测距公式,取行波波速为计算波速2.981 13×105 km/s,得到最终的测距结果为25.01 km,误差为10 m。
下面将自适应S变换和S变换在不同区段上的故障
测距结果进行比较。故障类型为A相接地故障,过渡电阻20 Ω,线路中包含60 dBW的噪声。其中,自适应S变换采样频率为10 MHz,S变换采样频率为100 kHz。测距结果如表1、表2所示。


可以看出,采用了自适应S变换的故障测距算法,在保证系统实时性的基础上,可以通过提高采样频率,减少测距误差,在准确度与实时性上较传统S变换算法都具有很大优势。
4结论
本文在S变换的基础上,提出了将自适应S变换与故障定位结合的新方法,能够大大减少所需的存储空间以及计算量,大幅度提高采样频率,提高了定位的准确度,同时对含噪情况下该方法的可靠性加以验证。尽管仿真结果比较令人满意,但应当注意的是实验只是在理论基础以及理想的模型上进行的,实际应用效果有待进一步考证。
参考文献
[1] 要焕年, 曹梅月. 电力系统谐振接地[M]. 北京:中国电力出版社, 2009.
[2] 贺家李, 宋从矩. 电力系统继电保护原理[M]. 北京:中国电力出版社, 1994.
[3] 徐伟宗. 采样频率对行波测距影响的仿真分析[J]. 电力系统及其自动化学报, 2014, 26(6):76-80.
[4] 易吉良. 基于S变换的电能质量扰动分析[D]. 长沙:湖南大学, 2010.
[5] 束洪春. 电力工程信号处理应用[M]. 北京:科学出版社, 2009.
[6] CHU P C. The S transform for obtaining localized spectra[J]. Marine Technology Society Journal, 1995, 29(4):28-38.
[7] PINNEGAR C R, MANSINHA L. Time frequency localization with the Hartley Stransform[J]. Signal Processing, 2004, 84(12):2437-2442.
[8] 易吉良, 彭建春, 谭会生. 采用不完全S变换的电能质量扰动检测方法[J]. 高电压技术, 2009, 35(10):2562-2567.
[9] 李立, 易吉良, 朱建林. 采用改进不完全S变换估计电能质量扰动参数[J]. 电工技术学报, 2011(6):187-193.

