李准1，潘幸子1，孙水发1,2，李娜1,2

　　（1. 三峡大学 水电工程智能视觉监测湖北省重点实验室，湖北 宜昌 443002；2. 南京师范大学 江苏省三维打印装备与制造重点实验室,江苏 南京 210042）

　　摘要：点云配准是通过匹配具有重叠部分的数据集，将不同坐标下的三维数据集变换到同一坐标系下，得到旋转变换矩阵和平移向量。通过各种约束条件，建立适当的模型。刚性配准在变换过程中不会发生形变，而非刚性配准需要考虑形变等问题。刚性配准和非刚性配准在约束条件上有所不同，文章从特征、显著性、正则化等约束条件，对刚性和非刚性配准约束条件进行了研究讨论。

　　关键词：配准；刚性；非刚性；形变；约束

　　中图分类号：TP391文献标识码：ADOI： 10.19358/j.issn.16747720.2016.23.003

　　引用格式：李准，潘幸子，孙水发，等. 三维点云配准约束条件综述［J］.微型机与应用，2016,35（23）：12-14，17.

0引言

　　点云配准是通过匹配具有重叠部分的数据集，寻求不同数据集之间的一致性对应关系，将不同坐标系下的三维数据集变换到同一坐标系下，最终得到被扫描物体的完整点云集。但在现实应用中，由于三维扫描技术的局限性，不同的数据集通常是从不同的观测点获取，每一个观测点都处在不同的坐标系下，因此表面配准是三维数据获取的重要部分，也是计算机视觉［1］、计算机图形学［2］等的基础。点云配准分为刚性配准和非刚性配准。刚性配准，即被扫描物体不发生形变等变化；非刚性变换允许被扫描物体发生诸如形变、清晰度等变化。

　　刚性配准，在数据的采集过程中会遇到很多困难，包括噪声、离群点和数量有限的重叠部分等情况；非刚性配准不仅要克服刚性配准的各种问题，还要考虑被扫描物体的形变等问题，非刚性配准通常缺乏足够的一致性对应关系，所以需要定义更多可靠的一致性对应信息进行配准。

　　随着三维激光点云扫描技术与点云数据处理技术的不断进步，不论是刚性配准还是非刚性配准，都可以通过建立适当的约束条件加以解决。

1刚性配准

　　刚性变换中，以寻求满足N个数据点的旋转矩阵R以及平移向量t组成的刚体变换为目标，对于两片具有重叠部分的不同点云集P和Q，使其满足qi=Rpi+t。其中，pi为点云集P上任意点，qi为pi在点云集Q的对应点。对于刚性配准的各种算法，大都是通过各种约束条件，建立配准算法模型。下面对刚性配准约束条件进行研究讨论。

　　1.1变换约束

　　最近点准则可以约束潜在的一致性对应。该方法是在一个刚体变换中，选取最近点qi∈Q作为pi的匹配，以完成最终配准。在标准迭代最近点算法ICP中，通过最小化函数

　　进行约束。迭代最近点算法对于初始化要求较高，并且在每一次迭代时更新旋转矩阵R和平移矩阵t。由于ICP算法的良好性能，众多学者在此基础上提出了很多改进算法来提高计算速度以及鲁棒性。

　　1.2特征约束

　　刚性变换中，不同视角下被扫描物体曲面几何特性保持不变。常用的几何特征如曲率、法矢量等，多种不同的特征可以形成一个特征向量。由于特征维度越高匹配所有特征的概率越低，所以高维特征向量能够简化数据。但此类方法要求被扫描物体特征较明显且容易提取，并且在特征提取过程中会花费较多的时间。KASE K等人［3］使用扩展高斯曲率和一个匹配率方程来判断对应点集之间的差异，扩展高斯曲率定义为：

　　其中pi与qi为不同点云集的对应点，k1、k2为主曲率。在配准过程中通过提取包括旋转图像、平均曲率等特征，可以极大地简化数据量，从而提高配准效率。

　　1.3显著性约束

　　显著性区域是一些与其附近区域性质具有很明显差异的区域。显著性可以用来衡量物体表面的局部信息，以及完成对关键点或关键区域的检测。在刚性配准中，显著性通常与特征结合在一起来减少对应关系的空间以及潜在的不匹配性，最终获得更可靠一致性对应以完成配准。常用的显著性措施包括：几何尺度空间分析、基于视觉显著性的尺度和曲率、多尺度滑动和最大稳定域极值等。

　　1.4正则化约束

　　正则化通过对目标函数增加惩罚项来进行约束。正则化约束包含先验信息，在优化时避免了局部最小值的出现，提高了搜索效率。GOLD S和RANGARAJAN A［4］将刚性配准作为一个连续优化问题，同时处理刚性变换和一致性对应。该方法基于最近点准则，定义基于熵的正则化项：

　　其中，M是所有一致性对应的潜在匹配矩阵。由熵的定义可知，当所有的点匹配是等可能的，熵达到最大值。该方法有助于目标函数对错误表面的分解。

　　1.5搜索约束

　　搜索约束主要针对配准效率，包括局部化方法和分层搜索的方法。JOST T等人［5］进一步结合上述由粗到精等级搜索技术，使用下采样技术加快ICP的迭代速度，该方法逐步细化以至得到更可靠的一致性对应。Krsek对表面结构特征进行分层，该方法根据一些显著点估计欧式变换，然后利用曲率和表面重新定义变换。

　　对于刚性配准，从刚性变换、特征、显著性、正则化和搜索约束进行了研究讨论，众多学者以此解决了点云的刚性配准。

2非刚性配准

　　非刚性配准涉及形变等因素，在表现形式上与刚性变换有所不同。MITRA N J等人［6］提出时空位移模型：

　　其中，(Rj,tj)是旋转和平移变换，τj是沿时间轴的变换，上述变换在时空域里连续的j帧数据是一致的，但该方法需要在时域和空域密集地采样。下面对非刚性变换约束进行研究讨论。

　　2.1形变约束

　　非刚性变换中，形变模型本身可能产生约束。设(M,)为具有度量张量的黎曼流形。拉普拉斯贝特拉米操作符Δ由决定，定义表面距离的形式：

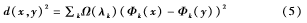
　　其中λk和Φk是Δ的特征值和特征函数。Bronstein通过路径长度t衡量两个点的连通程度，定义扩散距离Ω(λk)=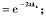Fouss基于扩散距离规模不变的形式，定义的交换时间距离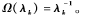

　　2.2特征约束

　　诸如旋转图像、平均曲率、积分描述符等特征一直应用于求取非刚性配准一致性对应。Sun基于热扩散点提出热内核签名，该方法具有等距不变特性、多尺度、多信息和稳定等特点。Me′moli通过Gromov-Wasserstein距离，关联并重新解释HKS与其他的光谱形状配准技术。经众多学者研究发展，HKS的变式相继被提出，Bronstein和Kokkinos使用傅里叶变换避免尺度差异，并定义了尺度不变形式的热内核签名。

　　2.3显著性约束

　　与刚性变换中的显著性约束类似，在非刚性变换中也可以将显著性应用于配准。KIM V G等人［7］使用形变不变函数的极值，利用积分测地距离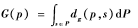定义显著点。如果p距离其他网格较远，G(p)较大，该方法对于表面的细节变化具有稳定性。LITMAN R等人［8］利用最大稳定极值区域检测非刚性外形稳定区域。

　　2.4正则化约束

　　在非刚性配准中，物体表面具有更多的高频信息，为保护形变时的细节清晰度等信息，往往需要更多的自由度来描述物体的形变。但过多的自由度会产生不必要的噪声，大多数非刚性配准使用正则化来进行约束。LI H等人［9］对每个节点使用仿射变换A={123}，模拟物体的表面细节。为保证整个变形模型与关节一致，最大化局部刚度为：

　　LI H等人避免了遮挡造成的空洞影响，最小化：

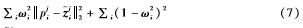
　　其中是深度值。

　　2.5运动包络约束

　　由于运动包络是由点的轨道线垂直于其法线场，点云集的一致性对应可以由时空表面计算得到。MITRA N J在刚性和非刚性校正中考虑到时空表面，利用瞬时运动学定义最小化速度场和法线场数量积。对于非刚性校正，进行下采样，并计算局部瞬时时空速度，使用正则化将得到的计算结果应用于邻近点。但时空表面需要非常密集的空间和时间采样数据。

　　对于非刚性配准，从形变、特征、显著性、正则化和运动包络约束进行了研究讨论，搜索约束与刚性配准中的类似，在此不加赘述。众多学者在此基础上对非刚性配准进行了深入的研究探索。

3结论

　　文章陈述了刚性配准和非刚性配准的约束条件，通过整合约束条件，建立相应的模型，运用计算机可以求解旋转变换和平移向量，以完成点云的配准。

　　经过众多学者的研究，刚性配准的很多问题已经解决。刚性配准正面向应用程序，开发能够处理具有不同水平细节和至关重要规律性结构的大型数据的刚性配准技术，与3D打印联系将更紧密。随着技术的进步，手持扫描设备将向小型化、智能化发展，针对这些无处不在的设备，实时技术是一个发展新方向。

　　对于非刚性配准的研究，还处于初始阶段。独立建立极具意义和自然的一致性对应，选择适当的变形表示和评价非刚性方法的适当工具是非刚性配准的两大难题。由于现实世界中各种各样的转换，一致性对应和先验信息的缺乏是困扰众多研究者的难题。随着点云数据处理技术的不断进步，具有先验信息的假设将日益完善。这些技术将使非刚性配准更加成熟。

　　参考文献

　　［1］ 陈海松, 李益民, 韩秀清. 基于计算机视觉的高精度图像拼接［J］. 微型机与应用, 2011, 30(15):38-40.

　　［2］ 伍龙华, 黄惠. 点云驱动的计算机图形学综述［J］. 计算机辅助设计与图形学学报, 2015, 27(8):1341-1353.

　　［3］ KASE K, MAKINOUCHI A, NAKAGAWA T. Shape error evaluation method of free form surfaces［J］. ComputerAided Design, 1999, 31(8):495-505.

　　［4］ GOLD S, RANGARAJAN A. A graduated assignment algorithm for graph matching［J］. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1996, 18(4):377-388.

　　［5］ JOST T, HUGLI H. A multi resolution ICP with heuristic closest point search for fast and robust 3D registration of range images［C］.3 D Digital Imaging and Modeling, 2003. 3DIM 2003. Proceedings. Fourth International Conference on. IEEE, 2003: 427-433.

　　［6］ MITRA N J, FLRY S, OVSJANIKOV M, et al. Dynamic geometry registration［C］.Symposium on Geometry Processing. 2007: 173-182.

　　［7］ KIM V G, LIPMAN Y, FUNKHOUSER T. Blended intrinsic maps［C］.ACM Transactions on Graphics (TOG). ACM, 2011, 30(4): 76-79.

　　［8］ LITMAN R, BRONSTEIN A M, BRONSTEIN M M. Diffusiongeometric maximally stable component detection in deformable shapes［J］. Computers & Graphics, 2011, 35(3): 549-560.

　　［9］ LI H, ADAMS B, GUIBAS L J, et al. Robust singleview geometry and motion reconstruction［C］.ACM Transactions on Graphics (TOG). ACM, 2009, 28(5): 89-97.