顼聪，陶永鹏
（大连外国语大学 软件学院， 辽宁 大连 116044）
摘要：局部二值模式(LBP)算法是人脸识别领域中的经典算法,能够捕捉局部的细节特征，但其鲁棒性和识别率易受外部环境变化的影响。文章深入研究了LBP算法，从LBP算子、直方图特征提取对传统LBP算法进行改进，并结合LIOP编码方法，进一步提出了增强局部量化模式（ELQP）的人脸识别算法。实验结果表明，改进的LBP算法具有更高的识别率和较强的鲁棒性。
中图分类号：TP391文献标识码：ADOI： 10.19358/j.issn.16747720.2016.23.005
引用格式：顼聪，陶永鹏. 基于改进的LBP人脸识别算法的研究［J］.微型机与应用，2016,35（23）：18-20,27.
0引言
人脸识别，特指利用分析比较人脸视觉特征信息进行身份鉴别的计算机技术。研究人脸识别重点在于对核心算法的研究,通过算法的改进使识别结果具有实用化的识别率和识别速度。当前人脸识别领域中，主要有以下核心算法研究［1］：（1）通过积分方式进行欧式距离表示,形成的基于几何特征的算法，例如MIT的Brunelli和Poggio科研团队。（2）利用模板匹配算法进行人脸特征提取（如眉毛、眼睛轮廓的特征提取），例如Harvard大学SmithKettlewell眼睛研究中心。然而目前面临的主要问题是外界环境的不断变化对人脸识别产生了巨大影响，加大了识别的难度。如何提出新算法或改进原有的算法进行有效的人脸特征提取是目前人脸识别技术研究的重点。
早期的研究提出了Eigenface方法［2］，主要是利用主成分分析（PCA）进行人脸特征提取，形成特征脸，因为初步提取的描述人脸外在变化的特征脸维度较高，所以要进行降维处理。在此基础上进一步提出了Fisherface［3］方法，先应用PCA对特征向量进行降维，然后使用线性判别分析(LDA)使特征的类内差异减小并增大类间差异。但是这些基于全局特征的方法对于表情、光照、遮挡这些变化十分敏感，于是基于局部特征的人脸算法逐渐成为新的研究热点。
1LBP的算法的改进
1.1LBP理论
局部二值模式(LBP)算法是一种典型的基于局部特征的识别算法［4］。LBP局部二值模式是一种基于灰度值比较的局部纹理结构表示方法，与灰度特征相比表示能力更强。它对于边缘、角点和平滑变化的图像区域都能良好地表示出来。对于任意图像I来说，LBP通过比较中心像素点和邻域像素点的值来对图像进行重编码，其定义如下：
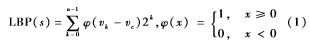
其中φ(x)为阈值化函数，只有当x的值大于等于0时函数值为1，否则函数值为0；n代表LBP编码总的邻域点数；k表示第k个邻域点；c代表中心像素点。
LBP算法计算方法简单，不涉及到复杂的运算，但是本身存在两个缺陷：
第一,随着LBP的邻域点数量增加，LBP的主模数量会成指数形式增加。
第二,LBP编码虽然有一定的灰度不变性和旋转不变性，但是对姿态变化和光照变化等外界环境依然不够鲁棒。
1.2LBP算子的改进
对于LBP算法的改进，目的是克服原有算法的不足，提高在复杂外界环境下人脸的识别率。
由于基于局部特征提取框架主要分为三个部分，因此主要的改进方向有：图像滤波、模式采样、模式编码三个。
1.2.1图像滤波上的改进
在不同的光照环境下得到的人脸图像存在显著的差异，为了消除这种差异需要对图片进行预处理。具体来说就是对于图像I使用滤波核w进行滤波处理，得到图像f(I)，然后对f(I)进行LBP编码。增强图像细节。
1.2.2模式采样的改进
LBP方法只使用了邻域点与中心像素点的大小关系，没有利用上邻域点之间的大小关系，而且对于邻域点之间的权重是相等的。因此如何利用邻域点之间的大小关系进行编码是重点解决的关键技术问题。考虑到局部序数模式算法可以对邻域点按照一定的关系排序，因此本文采用该算法去改善模式的编码。
1.2.3模式编码上的改进
LBP编码的主模数与邻域点数之间存在指数关系，然而为了增强判别能力不得不使用较大的邻域点数。因此如何降低主模数量是重点解决的关键技术问题。针对这个问题HUSSAIN S U提出了LQP，通过使用离线K均值距离建立一个码本，并将二进制序列分成K个子类来编码主模。
1.3直方图特征提取
改进LBP算子后，需要进一步进行直方图下的特征提取。如图1所示。
（1）直方图特征度量
基于图像分块的直方图特征提取是一种局部建模方法，计算得到空间直方图对于表情、饰物、光照、姿态等的变化不敏感。为了对直方图特征进行相似度比较，因此需要使用一定的度量标准。对于图片的直方图特征表示来说，传统的欧氏距离度量不再适用于直方图相似度的计算，直方图相交距离［5］可以有效表示其直方图特征的类似状况，因此本文加以采用，并给出直方图相交距离的数学定义：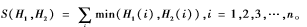
（2）直方图权重度量方法
人脸不同的部位对于身份的辨别具有不同的重要性。不同的直方图特征对应的判别能力也不同，因此需要对不同的直方图块赋予不同的权重。整体的直方图特征就是由每一个区域的直方图连接起来的。为了体现不同直方图块在整体人脸的不同部位的重要性，需要进行权重的分配。而目前关于权重的设置并没有一个很好的方案，人工指定的方法过于复杂，对于各个区域权重的取值过于随意，取值全靠经验。因此针对不同的直方图特征对应的判别能力的不同，本文改写了上面直方图相交的公式，加入了权重后其直方图相交距离为：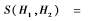
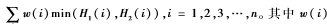就是第i块直方图对应的权重值。
（3）直方图特征的降维方法
直方图特征维数过高不利于后续的识别和实际应用中实时计算的要求，因此有必要对直方图特征进行降维处理。本文利用特征降维法PCA［6］，算法步骤为：①计算散布矩阵S；②计算散布矩阵S的本征值和本征向量；③按本征值的大小，从大到小对其对应的本征向量进行排序；④选择其中最大的d个本征值对应的本征向量，并将其作为投影向量，构成D×d投影矩阵W。
测试结果如图2所示。
图2（a）是原始人脸图像，图2（b）是采用分块的 LBP图像的空间增强直方图算法进行特征提取的人脸图像，图2（c）是经过 PCA 降维的特征图像。可以看出经过 PCA 降维的人脸的局部细节特征依然保留，但数据量降低，说明经 PCA 降维的特征提取取得了良好的效果。通过降维后人脸图像特征矩阵识别将转化为样本分类的求解问题，本文则通过构建最小支持向量机来进行分类。
2增强局部量化模式（ELQP）人脸识别算法
2.1概述
因LBP的邻域编码能力比较弱化，依然影响最终人脸的识别，所以本文在改进LBP算法的基础上进行更进一步的研究，提出增强局部量化模式（ELQP）的人脸识别算法。
LIOP［7］是用邻域序数关系代替LBP的邻域编码，具有更强的判别能力，LQP是一种通过查表的方式对特征向量进行编码的方法，可以在不增加计算复杂度的情况下对更大的邻域进行采样编码。因此结合LIOP和LQP的优点提出了ELQP算法进行人脸识别。
2.2LIOP主模数指数级增加的解决
LIOP也会遇到随着邻域点数的增加，主模数呈指数级增加的问题。应用局部量化模式可以在一定程度上解决这个问题。局部量化模式通过预先建立的查找表来对特征向量进行量化编码，设计分为训练和编码两个阶段。训练阶段提取所有图像的邻域特征向量，应用K均值聚类算法得到一个码本。编码阶段使用查表法将特征向量编码成码本中对应的码字，从而获得LQP编码图。
2.3融合LIOP和LQP的特征提取方法
增强局部量化模式是融合LIOP与LQP的特征提取方法。如何进行融合是问题处理的关键。本文设计的ELQP编码选用16个邻域点构成的邻域向量计算离线码本。为了降低计算量，此处将图像分成6×6的子块，分别为每一个子块计算一个码本。邻域点的定义如图3所示。
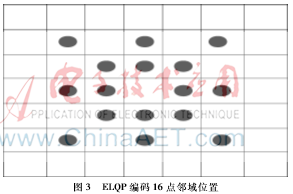
2.4似度量与降维方法
所有图像提取特征向量后都需要比较图像之间的相似度。考虑到识别过程的计算效率，针对直方图特征一般使用直方图相交度量来计算相似度。如何定义两个直方图的特征向量并计算直方图相交距离是重点解决的关键问题。同时利用Fisher［8］进行特征向量的权重的分配。对于降维处理本算法采用了WPCA［9］降维。
3实验参数与结果
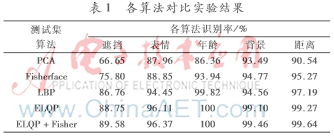
实验中的所有算法使用直方图相交度量的结果如表1所示。表2给出了各算法的特征提取时间和维数。
从表1的实验结果发现，本文方法的识别率在遮挡、表情、年龄、背景和距离5个测试集上的结果优于与之对比的PCA、LBP、Fisherface算法。
表2的结果表明本文算法ELQP在高维度下提取时间用时很少，效率高于PCA及Fisherface算法。这说明了本文算法的实用性较强。
4结论
人脸识别是一个具有巨大挑战力的课题，虽然近十几年来得到了非常大的关注，也取得了很多的研究成果，但是仍然没有在本质上有很大的突破。本文通过分析局部二值模式(LBP)算法在人脸识别中的问题，针对LBP算子在图像滤波、模式采样、模式编码三个方面进行了改进，以提高在多变环境下LBP算法的人脸识别率。在改进的局部二值模式(LBP)算法基础上，本文针对LBP编码时邻域特征向量的关系进行深入研究，结合LIOP和LQP算法的优点，提出了增强局部量化模式（ELQP）算法。并通过实验进行了验证，证明了本算法的优越性。
参考文献
［1］ 山世光.人脸识别中若干关键问题的研究［D］. 北京:中国科学院计算技术研究所,2004.
［2］ 张宝昌.人脸特征提取和非线性识别方法的研究［D］.哈尔滨：哈尔滨工业大学, 2006.
［3］ ZHAO W, CHELLAPPA R, PHILLIPS P J, et al.Face recognition: a literature survey［J］.ACM computing surveys (CSUR), 2003, 35(4): 399-458.
［4］ 雷震.人脸识别关键问题和算法研究［D］. 北京:中国科学院计算技术研所,2010.
［5］ HARMAON L D, KHAN M K, LASCH R, et al. Machine identification of human faces［J］. Pattern Recognition, 1981, 13(2): 97-110.
［6］ CHELLAPPA R, WILSON C L, SIROHEY S. Human and machine recognition of faces: a survey［J］. Proceedings of the IEEE, 1995, 83(5): 705-741.
［7］ PENTLAND A, MOGHADDAM B, STARNER T. Viewbased and modular eigenspaces for face recognition［C］.Computer Vision and Pattern Recognition, 1994. Proceedings CVPR'94., 1994 IEEE Computer Society Conference on. IEEE, 1994: 84-91.
［8］ BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection［J］. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1997, 19(7): 711-720.
［9］ 谢术富.人脸识别中的局部表示方法研究［D］.北京:中国科学院计算技术研究所,2010.