王博林1， 闫德勤2， 楚永贺2

　　（1.辽宁师范大学 数学学院，辽宁 大连 116029；2.辽宁师范大学 计算机与信息技术学院，辽宁 大连 116081）

       摘要：在人脸图像识别中人脸图像数据中有很多是稀疏的，对于稀疏数据的降维是流形学习算法面临的一个问题。为了有效地从高维图像数据中提取人脸图像的敏感信息，提高人脸识别的速度，文章提出了一种基于流形学习的有监督稀疏排列的局部保持投影算法(SSLPP)的极端学习机(ELM)。

　　关键词：流形学习；极端学习机

　　中图分类号：TP18文献标识码：ADOI： 10.19358/j.issn.16747720.2016.23.012

　　引用格式：王博林， 闫德勤， 楚永贺. 基于稀疏排列的LPP和ELM的人脸识别［J］.微型机与应用，2016,35（23）：42-45.

0引言

　　近年来在流形学习的基础上研究人员提出了不同的降维算法，例如，局部保持嵌入(Locally Linear Embedding, LLE)［1］、拉普拉斯特征映射(Laplacian Eigenmaps, LE)［2］，这些非线性方法在人脸图像识别中取得了理想的效果，然而人脸图像数据往往具有非常高的维数,利用这些非线性方法是非常耗时，对如何构建测试数据的邻接图关系是未知的。为了解决上述非线性方法的耗时问题，研究人员提出了有监督的邻域保持嵌入(Supervised Neighborhood Preserving Embedding, SNPE)［3］、判别信息增强的邻域保持嵌入(DiscriminantEnhanced Neighborhood Preserving Embedding, DNPE)［4］、局部最大间隔判别嵌入(Local Maximal Margin Discriminant Embedding, LMMDE)［5］等能够很好地提取人脸图像数据的判别信息，并且解决了非线性方法的耗时问题。目前在人脸图像识别中降维算法面临的问题是：基于流形学习的各种算法对人脸图像数据的判别信息的提取效果不佳，极大地影响着极端学习机的分类性能。降维算法的有效性取决于对人脸图像数据判别信息的有效提取。稀疏性是人脸图像数据的属性之一，影响着降维算法的有效性。

　　近年来HUANG等人［6］基于单隐层前馈神经网络（SingleHidden Layer Feedforward Networks,SLFNs）结构提出了极端学习机（Extreme Learning Machine,ELM）。ELM训练速度快，避免了传统SLFNs学习方法收敛速度慢及陷入局部极小解的可能。ELM是一种基于单隐层前馈神经网络（SLFNs）的结构，它随机选择输入权值和分析确定SLFNs的输出权值，具有更好的泛化能力和更快的学习速度，避免了琐碎的人为干预，使得它在在线和实时应用中具有较高的效率。然而在人脸识别问题中由于人脸图像数据往往具有非常高的维数，从而使ELM的识别率下降和分类速度变慢，为此本文提出了基于流形学习的极端学习机。本文的创新点如下：（1）将流形学习的理论与ELM结合起来，进而提高人脸识别的识别率和识别速度； （2）考虑到人脸图像数据的稀疏性，为此利用人脸图像数据的统计信息动态确定局部线性化范围，在LPP算法的基础上依据数据的分布提出一种有监督稀疏排列的局部保持投影算法(SSLPP)。

1基于流形学习的SSLPP降维方法

　　对于稀疏的人脸图像数据样本集，样本间重叠的信息量非常少，为此本文通过扩大k邻域为k－N(i)区域对原始数据集进行区域信息加强，如图1所示，k－N(xi)区域为N(xi)及其对应的k近邻点构成，这使得在数据样本集较少的情况下，同样能够实现重叠信息量非常充分的流形学习效果。

　　本文期望k－N(i)邻域降维后样本的邻域关系尽可能保持不变，则第i个样本邻域最小化目标函数为：

　　式 (1)中nc为第i个样本邻域所在类别的样本个数，将代入 式(1),最小化目标函数写为再对所有的样本邻域进行整合得到最终的优化函数为：

　　式(2)中c为所有样本的类别总数，uT为投影变换矩阵，依据文献［7］对LPP算法的推导过程如下：

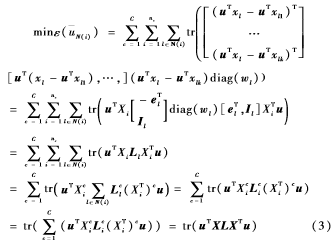
　　其中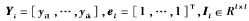的单位矩阵，L为拉普拉斯矩阵。SSLPP算法保持了LPP算法原有的框架，因此优化条件可写为：

　　其中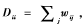利用拉格朗日乘子法对式(4)进行求解可得:

　　对矩阵XLXT和XDXT进行特征值分解，得到特征向量矩阵为U=［u1,…,uN］。从特征向量矩阵中选取的第2到第d+1个最小特征值对应的特征向量，即：［u2,…,ud+1］T，则由y=uTx得到SSLPP算法。

2ELM

　　对于N个不同的样本(xj,tj)可表示为X=(x1,x2,…,xN)T∈RD×N,其中tj=(tj1,tj2,…,tjm)T∈Rm，具有L个隐层节点激活函数为g(x)的ELM模型如下形式:

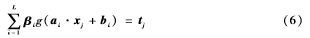
　　其中j=1,2,…,N，ai=(ai1,ai2,…,ain)为连接第i个隐层节点与输入节点的输入权值向量，βi=(βi1,βi2,…,βim)为连接第i个隐层节点与输出节点的输出权值向量，bi为第i个隐层节点的偏置值，ai·xj表示ai和xj的内积，tj=(tj1,tj2,…,tjm)T∈Rm为对应于样本xj的期望输出向量，对所有数据样本进行整合，式(6)可以改写为如下形式：

　　其中H是网络隐层节点输出矩阵，β为输出权值矩阵，T为期望输出矩阵：

　　当隐层节点个数与训练样本个数相同时(即L=N)，可以通过式(7)直接求矩阵H的逆矩阵得到最优的输出权值矩阵β，但大多情况下隐层节点的个数远小于训练样本的个数（即LN），此时矩阵H为奇异矩阵，利用最小二乘解的方法对式(7)进行求解：

　　其中,H+为矩阵H的广义逆。

　　为了提高传统ELM的稳定性和泛化能力，Huang提出了等式优化约束的ELM。等式优化约束的ELM的优化式子不仅最小化训练误差ξ，同时最小化输出权值β，因此等式优化约束的ELM目标式子可写为：

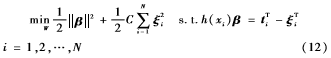
　　式(12)中ξi=(ξi1,…,ξ1m)T为对应于样本xi的训练误差向量，C为惩罚参数。式(12)的求解可通过拉格朗日方法转化为无条件最优化问题进行求解。因此ELM算法求解过程可总结如下：

　　（1)初始化训练样本集；

　　（2)随机指定网络输入权值ai和偏置值bi；

　　（3)通过激活函数［8］计算隐层节点输出矩阵H；

　　（4)计算输出权值,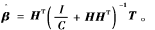

3实验结果及分析

　　2个不同人脸库数据参数设置如表1所示，人脸图像

　　如图2所示。为了证明所提出算法的有效性，在ORL实验中随机选取训练集个数为L={2，3，4，5}，剩余部分为测试集；在Yale B试验中随机选取训练集个数为L={5，10，20，30}，剩余部分为测试集，不同降维算法在不同维数下的识别率曲线及识别率如图3所示。

　　图3给出了ELM采用不同降维算法在ORL人脸数据上的识别率曲线。由图3可知ELM采用SSLPP算法的识

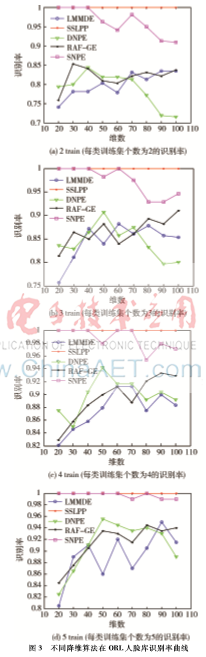
　　别率曲线达到了100%并且非常稳定，SNPE算法的识别率曲线随着位数据维数的增大出现了波动，DNPE算法、LMMDE和RAFGE算法［8］的识别率曲线随着数据维数的增大识别率也跟着增大，DNPE算法在ORL数据上表现出比较好的性质。

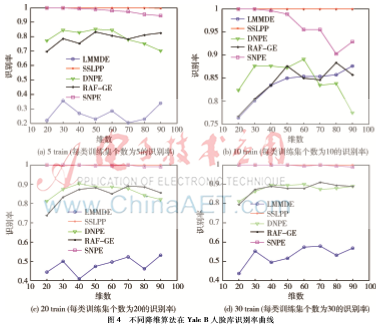
　　图4给出了ELM采用不同降维算法在Yale B人脸数据上的识别率曲线，由图4可知ELM采用SSLPP算法的识别率曲线明显高于其他算法并且非常稳定。

4结论

　　为了提高人脸识别的速度和准确率，本文提出了基于流形学习的极端学习机，通过与DNPE及LMMDE、RAFGE、SNPE算法的对比实验表明，本文所提出的方法在人脸识别速度和识别率上显著优于其他方法，因此，基于流行学习的极端学习机具有重要的现实的意义。

　　参考文献

　　［1］ROWEIS S T,SAUL L K, Nonlinear dimensionality reduction by locally linear embedding［J］.Science,2000,290(5500)：2323-2326.

　　［2］MIKHAIL B,PARTHA N.Laplacian eignmaps for dimensionality reduction and data representation［J］. Neural Computation, 2003,15(6)：1373-1396.

　　［3］Bao Xing,Zhang Li,Wang Bangjun,et al. A supervised neighborhood preserving embedding for face recognition［C］. International Joint Conference on Neural Networks,2014:278-284.

　　［4］Chai Yi,Yang Zhimin,Zhang Ke,et al. Discriminant enhanced neighborhood preserving embedding for dimensionality reduction［C］. IEEE Conference, Nov ,2013:255-210.

　　［5］Huang Pu,Tang Zhenmin,Chen Caikou,et al. Local maximal margin discriminant embedding for face recognition［J］. Vis. Commun. Image R., 2014(25):296-305.

　　［6］ Wang Dianhui，Huang Guangbin.Protein sequence classification using extreme learning machine［J］.Proceedings of International Joint Conference on Neural Networks, 2005(3):1406-1411

　　［7］ Huang Guangbin. An insight into extreme learning machines:random neurons,random features and kernels［J］. Cogn Comput,2014,6(3):376-390.

　　［8］ 冯林，刘胜蓝，张晶，等.高维数据中鲁棒激活函数的极端学习机及线性降维［J］.计算机研究与发展，2014，51(6)：1331-1340.