杨丹,何建农
(福州大学 数学与计算机科学学院,福建 福州 350116)
摘要:考虑到小波变换存在一些局限性,提出一种把非下采样Contourlet变换(NSCT)与脉冲耦合神经网络(PCNN)相结合的图像融合新方法。用NSCT变换从多尺度和多方向上分解配准后的原始图像。低频应用改进的边缘能量结合空间频率的融合方法;高频应用PCNN简化数学模型,其链接强度用改进的拉普拉斯能量和表示。并且选择点火映射图的点火次数与其标准差相结合的方法。最后经过NSCT逆变换得出融合图像。实验分析可知,与其他几种图像融合方法进行比较,新方法取得了更高质量的融合图像。
关键词:图像融合;非下采样轮廓波变换;脉冲耦合神经网络;边缘能量;拉普拉斯能量和
中图分类号:TP391文献标识码:ADOI: 10.19358/j.issn.16747720.2016.23.013
引用格式:杨丹,何建农. 一种新的结合NSCT和PCNN的图像融合方法[J].微型机与应用,2016,35(23):46-48,55.
0引言
图像融合是将由不同传感器获得的图像的重要信息进行互相补充,得到一幅含有更加全面信息的新图像,它能够更加准确地描述真实场景[1]。比较经典的是小波变换方法,不过它只有点奇异性,而且方向受到限制,因此不能解决高维问题。为了打破方向上的限制,相关学者又研究出了一些新方法,如Contourlet变换,它比小波变换处理的效果好,但其没有平移不变性。所以,CUNHA A L等[2]对Contourlet变换作了改进,提出非下采样Contourlet变换(Nonsubsanpled Contourlet Transform,NSCT),它有平移不变的性质。脉冲耦合神经网络(PulseCoupled Neural Network,PCNN)是Eckhorn提出来的,它对图像融合领域产生了重要影响。
1NSCT变换
NSCT变换是由两个重要的部分构成,它们分别为非下采样金字塔滤波器组(NSP)和非下采样方向滤波器组(NSDFB)[3]。用NSP从多尺度上分解输入图像,获得低频子带、高频子带;用NSDFB从多方向上分解高频子带,获得方向子带。重复进行这两个操作就是对图像进行了NSCT变换。NSCT变换的工作流程中不包含上采样和下采样的环节,因而拥有平移不变的性质,这是它与Contourlet变换的重要区别。图1为NSCT的结构示意图。
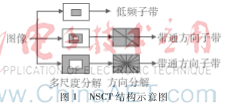
2NSCT与PCNN相结合的图像融合方法
2.1融合步骤
本文提出一种NSCT与PCNN相结合的新算法。具体步骤如下:
(1)利用NSCT变换分解原图像A与B,获得高低频系数。
(2)低频使用的是改进的边缘能量与空间频率相结合的融合策略;高频引入PCNN模型,其链接强度使用的是改进的拉普拉斯能量和,选择点火映射图的点火次数与其标准差相结合的融合策略。
(3)对融合后的低频系数CF(i,j)和高频系数Ck,lF(i,j)作NSCT逆变换,取得融合图像F。
2.2低频融合规则
利用NSCT分解之后的低频域表示图像的大体轮廓,它是对真实场景的近似描述。因为空间频率可以表征图像的活跃状态,边缘区域能量能够反映其边缘特征。参考文献[4]和[5]使用边缘能量与空间频率相结合的融合策略,能够有效地保留图像的边缘细节信息,提高图像的清晰度。改进的边缘能量定义:
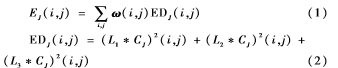
式(1)中,ω(i,j)为窗口加权系数矩阵,为了突出窗口中心像素与其变化边界,本文选取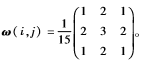 式(2)中,L1、L2、L3为方向滤波算子,其值分别为:
式(2)中,L1、L2、L3为方向滤波算子,其值分别为:
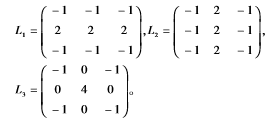
其中,EJ(i,j)为原始图像J在像素(i,j)处的边缘能量,J=A、B;CJ表示图像的低频系数;表示卷积。
改进的空间频率定义为:
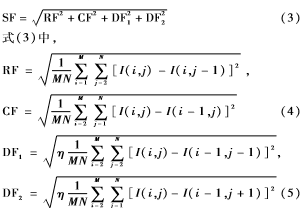
其中,SF为空间频率;RF、CF分别表示行频率和列频率;DF1、DF2分别表示对角线为45°和135°时的频率;I(i,j)为像素(i,j)处的灰度值;η=0.707。
加权系数是通过对S函数[6]改进得到的,本文改进的S函数为:
w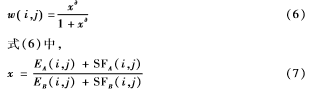
其中,为收缩因子,本文取为5。
最终获得的融合系数为:
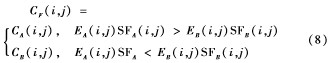
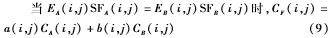
其中,加权系数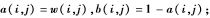 为融合图像F在像素(i,j)处的低频融合系数。
为融合图像F在像素(i,j)处的低频融合系数。
2.3高频融合规则
PCNN是由一些神经元组合成的网络,每个神经元都是由接受域、调制部分和脉冲产生器三个成分动态非线性地构成[7]。本文使用的是PCNN的简化模型,其数学模型如式(10)所示:
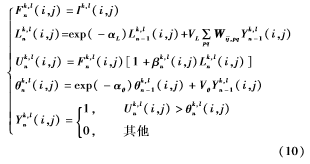
其中,(i,j)是神经元所在的位置;Ik,l(i,j)为外部的输入刺激;Fk,ln(i,j)为第n次迭代时的反馈输入;Lk,ln(i,j)为链接输入;Uk,ln(i,j)表示内部活动项;θk,ln(i,j)为动态阈值;αL、αθ为链接输入和动态阈值的时间常数;VL和Vθ分别为Fk,ln(i,j)和Lk,ln(i,j)的放大系数;p、q为链接范围;Wij,pq为神经元之间的链接矩阵;βk,ln(i,j)为链接强度;Yk,ln(i,j)表示输出项。Uk,ln(i,j)>θk,ln(i,j)时,输出项Yk,ln(i,j)=1,则表示发生了一次点火;Tk,ln(i,j)为总点火次数。
高频系数表示的是图像的细节纹理信息,人的视觉更倾向于对这部分信息的关注。考虑到PCNN方法能够更好地提取图像的细节信息,所以本文在处理高频方面引入PCNN模型。参考文献[8]及[9],在PCNN的模型中,其刺激输入采用高频系数,链接强度采用改进的拉普拉斯能量和,融合规则选取点火次数与其标准差相结合的方法。此方法能够更加充分地展现图像的细节纹理特征。改进的拉普拉斯能量和的定义:

其中,NSMLk,lJ(i,j)为输入图像J在k尺度l方向位于像素(i,j)处的拉普拉斯能量和,J=A、B;Ck,lJ(i,j)为输入图像J的高频系数。

计算点火映射图的标准差为:
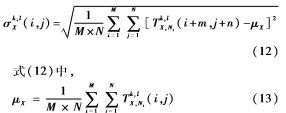
其中,X=A、B;σk,lX为点火映射图位于k尺度l方向上的标准差;Tk,lX,N1为点火次数;μX为点火次数均值。
本文选择PCNN的点火映射图的点火次数与其标准差相结合的融合方法:
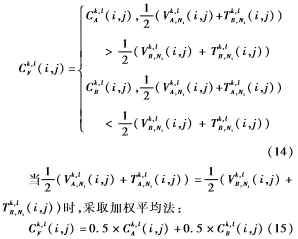
其中,Ck,lF(i,j)为融合图像F在k尺度l方向上的高频系数。
3仿真实验结果和分析
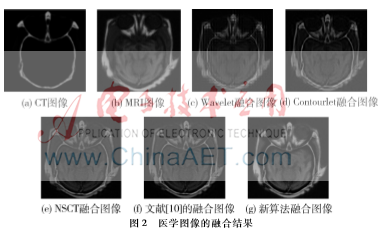
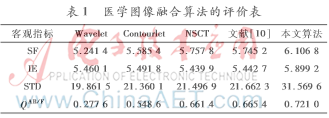
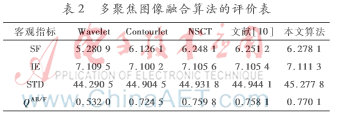
本文选择了两组精确配准后的多聚焦图像和医学图像进行分析。通过用新算法与其他4种算法进行比较,证明新算法的有效性。其他4种算法分别为:小波变换算法(WT)采用低频取平均,高频取大的融合方法;Contourlet变换算法中低频采用取平均,高频能量取大;NSCT算法采取低频取平均,高频采取绝对值取较大者的方法;文献[10]中低频选择加权平均,高频引入PCNN,其链接强度为拉普拉斯能量和。
从人眼视觉上对两组图像分别进行分析。观察图2,图2(c)出现明显的频谱失真现象,整体比较模糊。图2(d)效果有所改善,但是骨骼、软组织等信息损失较为严重。图2(e)和(f)清晰度有所提高,但是具体细节纹理信息不够清晰,图(f)比(e)的效果好些。图2(g)为新方法的结果,图中的骨骼结构、软组织部分很清楚,亮度合适,有利于人眼观察。
观察图3,图3(c)中右边的条形码出现失真现象,图中的字迹很模糊。图3(d)比前者清晰,但是边缘出现虚影。图3(e)和(f)的效果有所改善,但是图中的字迹不够光滑。图3(g)为新算法的结果,图中的所有字迹都很光滑、清楚,能够看出条形码的细节纹理。
本文还使用了4个客观指标进行评价。空间频率(SF)表示图像的空间活跃状态,数值越大其清晰度越高。标准差(STD)表示图像的对比度,取值越大其对比度越高。信息熵(IE)是反映图像保留下来的信息量的多少。QAB/F是表征边缘信息的指标,取值越靠近1表明其效果越好。对表1和表2进行分析可知,本文所提出的算法在这4个评价指标上都比其他4种方法的数值大,由此证明新算法所得到的融合图像效果是最好的。表
4结束语
综合NSCT变换与PCNN的优点,本文采取把两者相结合的图像融合新算法。本文的关键之处是对高低频融合方法的改进。低频应用改进的边缘能量与空间频率相结合的融合方法,高频应用PCNN模型,其链接强度为改进的拉普拉斯能量和。并且通过点火映射图的点火次数与其标准差相结合的方法选择高频融合系数。最后,对融合结果进行主观与客观评价,充分验证了新算法的有效性与可靠性。
参考文献
[1] 周渝人, 耿爱辉, 王莹,等. 基于对比度增强的红外与可见光图像融合[J]. 中国激光, 2014,41(9):223-229.
[2] CUNHA A L Da ,ZHOU J P ,DO M N. Nonsubsampled contourlet transform:theory,design, and applications [J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.
[3] 李美丽, 李言俊, 王红梅,等. 基于NSCT和PCNN的红外与可见光图像融合方法[J]. 光电工程, 2010, 37(6):90-95.
[4] WANG J, LI Q, JIA Z, et al. A novel multifocus image fusion method using PCNN in nonsubsampled contourlet transform domain[J]. Optik International Journal for Light and Electron Optics, 2015, 126(20):2508-2511.
[5] 郑伟, 孙雪青, 李哲. shearlet变换和区域特性相结合的图像融合[J]. 激光技术, 2015,39(1):50-56.
[6] 刘卫, 殷明, 栾静,等. 基于平移不变剪切波变换域图像融合算法[J]. 光子学报, 2013, 42(4):496-503.
[7] WANG Z B,MA Y D,CHENG F Y,et al.Review of pulsecoupled neural networks[J].Image and Vision Computing,2010,28(1):5-13.
[8] 李新娥, 任建岳, 吕增明,等. NSCT域内基于改进PCNN和区域能量的多光谱和全色图像融合方法[J]. 红外与激光工程, 2013, 42(11):3096-3102.
[9] CHAI Y, LI H, ZHANG X. Multifocus image fusion based on features contrast of multiscale products in nonsubsampled contourlet transform domain[J]. Optik International Journal for Light and Electron Optics, 2012, 123(7):569-581.
[10] 姜志.基于PCNN和NSCT变换的图像融合算法研究[D].杭州:浙江理工大学,2014.

