王宁章,闵仁江,许慧青
(广西大学 计算机与电子信息学院,广西 南宁 530004)
摘要:在自适应波束形成中,由于期望信号(SOI)导向矢量(SV)的误差、采样点数较少、训练数据中存在期望信号成分等原因,造成波束形成的性能严重下降。针对以上问题,提出了一种稳健波束形成方法。首先利用MUSIC算法和参数估计来重构不包含SOI的干扰噪声协方差矩阵,再通过利用相关系数来估计出期望信号导向矢量。仿真结果表明,该算法可以处理较大的方向误差,并且信噪比(SNR)在较大的范围内都可以得到比传统方法更佳的性能。
关键词:自适应波束形成;MUSIC算法;导向矢量估计
中图分类号:TN911文献标识码:ADOI:10.19358/j.issn.16747720.2016.23.018
引用格式:王宁章,闵仁江,许慧青. 基于干扰加噪声协方差矩阵重构的稳健自适应波束形成[J].微型机与应用,2016,35(23):62-64,68.
0引言
由于接收特定方向的信号,波束形成器可以认为是空间滤波器。它可以应用在不同的信号处理领域,包括雷达、声呐、医学成像、射电天文、无线通信等。作为数据依赖型波束形成器,自适应波束形成器通过抑制信号环境中的干扰和噪声,提取期望信号来调整权重矢量[1]。标准的Capon波束形成器(Standard Capon Beamformer, SCB)是大家所熟知的波束形成器,如果训练数据中不包含期望信号(Signal of Interest, SOI),那么SCB可以有最优的输出信干噪比(SignaltoInterfaceplusNoise Ratio, SINR)和高分辨率[2]。但是在实际的训练数据中经常存在SOI。在过去的几年中,许多稳健自适应波束形成器算法被提出,用来解决训练数据中存在的SOI和导向矢量(Steering Vector, SV)误差问题[3-5]。
在文献[3]中,GU Y等人提出使用Capon空间谱积分方法,其中积分区域为除SOI方向以外的角度区域,这种方法可以重构出干扰噪声协方差矩阵。通过解决二次约束二次规划(QCQP)问题来修正SOI假设的SV。这个方法在解决方向误差上会获得一个很好的性能。但是该方法的复杂度很高,并且需要知道精确的阵列结构信息。针对以上问题,HUANG L等人[4]提出把求不确定集合积分区域转变为求环不确定集合积分区域以及用离散求和方法来重构干扰噪声协方差矩阵。CHEN F等人[5]提出一种低复杂度的相关系数重构方法,通过直接使用采样协方差矩阵的特征向量与假设的SV有最大的相关性来解决SOI的SV估计问题。这几种方法都可以有效地提高波束形成性能,但是它们对于SOI和干扰信号存在相关性的问题都比较敏感,可能会造成SOI存在于重构的干扰噪声协方差矩阵中,造成性能急剧下降。本文使用MUSIC算法和参数化估计优化采样协方差矩阵和重构干扰噪声协方差矩阵,然后,对估计采样协方差矩阵进行特征分解和相关性分析,得出修正的SV。
1信号模型
考虑M个阵列元素组成的均匀线性阵列(Uniform Liner Array, ULA),并接受L个远场的窄带信号。窄带波束形成器的输出可表示为:

其中,k是时间参数,x(k)=[x1(k),…,xM(k)]T为一个M×1的阵列观测复数矢量,ω=[ω1,ω2,ω3,…,ωM]T是M×1的波束形成权重复数矢量,(·)T和(·)H分别代表转置和Hermitian转置,观测矢量(训练参数)可以表示为:
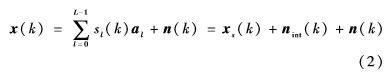
其中,sl(k)和al分别代表第l次信号的波阵面和对应的SV。xs(k)=a0s0(k),nint(k)=∑L-1l=1alsl(k)和n(k)分别是期望信号、干扰和噪声。
理论上的数据协方差矩阵可以表示为:
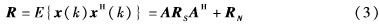
其中,RS和RN分别为信号协方差矩阵和噪声协方差矩阵,A为空间阵列的流型矩阵(导向矢量阵),且A=[a0,…,al-1]。对于空间理想的白噪声且噪声功率为σ2n,则有下式成立:
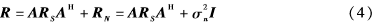
其中,I是M×M的单位阵。
为了测量波束形成的性能,在SOI不失真时的最大输出SINR可以定义为:

其中,
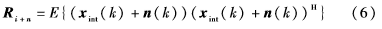
为M×M维干扰加噪声协方差矩阵,σ20为SOI的功率。使用波束形成最大输出SINR可以得到最优权重矢量:
上述问题的最优权重矢量为:

这个被称为最小方差无畸变波束形成器(Minimum Variance Distortionless Response, MVDR)或标准Capon波束形成器(SCB)。在实际应用中,实际的干扰噪声协方差矩阵Ri+n难以直接得到。因此,可以使用采样协方差矩阵来代替。

其中,K是快拍点数。当K很小时,和Ri+n的差距比较大,这会使得SOI被当成干扰而被抑制,特别是存在SOI导向矢量误差和高输入信噪比(Signal to Noise, SNR)时。因此估计协方差矩阵时,移除SOI部分是很有必要的。
2提出波束形成算法
本文提出了一种新的自适应波束形成算法来重构干扰噪声协方差矩阵,该方法采用MUSIC算法原理和参数化估计来优化采样协方差矩阵以及重构出干扰噪声协方差矩阵。同时,该方法利用相关系数来修正估计的SV。
2.1干扰加噪声协方差矩阵重构
为了重构干扰加噪声协方差矩阵,基于文献[6]的方法原理,公式(4)可以写成如下形式:

上等式可转化为:

其中,A=(AHA)-1AH为A的伪逆矩阵,RS为非对角化的信号协方差矩阵。当采样点数有限时会导致信号之间产生多余的相关性,或当信号之间已经存在相关性,这会使得输出SINR显著下降。可以使用矩阵的参数估计[7]来去掉多余的相关性,即对RS对角化得到Rd。由于只能得到采样协方差矩阵,则信号协方差矩阵可以表示为:

对上式对角化得到:
为了计算出,需要知道信号的波达方向和阵列流行结构。前文假设阵列结构是已知的,同时使用MUSIC算法的高分辨率搜索得到估计的信号方向。2n可以使用MUSIC算法中的最小特征值得到,把、d和2n代入式(4)中,得到采样协方差矩阵的参数估计:

上述为参数化估计后的采样协方差矩阵,该矩阵中的多余相关性已去除,在重构干扰噪声协方差矩阵时,计算结果更精确。在角度为θ时,功率可以使用e得到:

使用式(15),重构的干扰噪声协方差矩阵可以表示为:
其中,a(θ)是角度为θ的SV,为除期望信号角度区间外的其他区间,由于在实际情况下,期望信号的SV是不可获得的,通常利用估计的SV来代替实际的SV。所以,下面讲述期望信号估计SV的计算过程。
2.2期望信号SV的估计
在计算干扰加噪声协方差矩阵中,使用了MUSIC算法,通过MUSIC算法和估计的采样协方差矩阵e得到信号子空间和噪声子空间,如下所示:
其中,λi,i=1,…,M为e的特征值并从大到小排列,ei为特征值对应的特征向量。

其中,US为信号子空间,由于特征向量与信号的SV处于相同的空间,假设的期望信号SV可以被期望信号的特征向量来代替。可以使用相关系数的定义来找出符合情况的特征向量。由于期望信号SV与期望信号的特征向量有最大的相关性,可以用公式表示为:
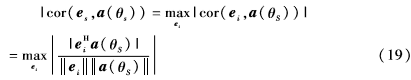
根据式(17)找到最大的相关系数对应的ei,即可以得到期望信号的特征向量es,考虑到期望信号SV的范数约束,估计的期望信号SV可以表示为:

因此,权重矢量可以写为:

由上可见,算法主要的复杂度是在进行特征分解时,复杂度为O(M3)。与前文提到的算法相比,算法的复杂度大幅降低,更有利于实际工程的应用。
3仿真结果
本文仿真中,考虑一个间隔半波长的全方向天线阵元M=10的均匀线阵。假设有估计的3个信号冲击信号分别为θ0=5°,θ1=20°,θ2=50°,噪声模型为一个复数高斯白噪声。第一个信号为期望信号,其他两个信号为干扰信号,它们的干噪比为10 dB。假设SOI和干扰的角度区域分别为Θ0=[θ0-5°,θ0+5°]、Θ1=[θ1-5°,θ1+5°]和Θ2=[θ2-5°,θ2+5°],除SOI的补集为=[-90°,0°)∪(10°,90°]。对于所有的情况,平均进行了200次MonteCarlo实验。
将本文的方法分别与对角加载算法[8]、特征空间算法[9]、最差性能优化算法[10]、重构算法[3]和低复杂度重构算法[5]相比较。在仿真中,假设从信号源接收的每个信号与实际信号存在[-5°,5°]的差别,这个假设可以表示随机的方向误差,再使用公式(8)计算出最优SINR。
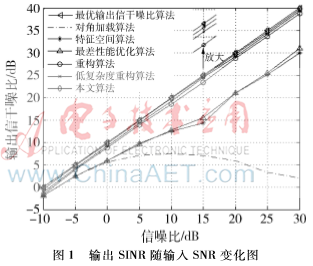
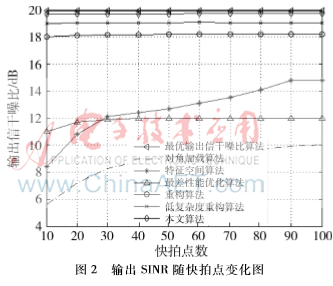
图1为存在信号方向误差的输出SINR随输入SNR变化图,快拍点数固定为30。从图中可以看出,对角加载算法、特征空间算法、最差性能优化算法在SNR较高时,输出SINR明显低于其他4种算法;本文提出的算法在低SNR和高SNR时都有高于其他算法的输出SINR,以SNR为15 dB为例,与最优输出SINR算法相差仅0.3 dB左右。因此,本文算法的高性能可以使得波束形成的稳健性有较大的提升。图2为存在信号方向误差的输出SINR随快拍点数变化图,SNR固定在10 dB,显而易见,在快拍数变化中,本文算法有稳定的输出SINR,并且比其他算法有更高的输出SINR。
4结论
本文提出一种新颖的干扰加噪声协方差矩阵重构的稳健算法,利用MUSIC算法和参数化估计,得到重构的干扰噪声协方差矩阵。其次,使用了最大相关系数来估计出期望信号的SV,该方法对于较大的干扰方向误差有较好的稳健性能。仿真结果表明:在采样点较少或输入SNR较低和较高时,该方法都存在一个最优的输出SINR。
参考文献
[1] REED I S, MALLETT J D, BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace & Electronic Systems, 1974, AES 10(6):853-863.
[2] SHEN S, YU W, SINICA A, et al. Detection, estimation, and modulation theory[M]. Publishing House of Electronics Industry, 2003.
[3] GU Y, LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7):3881-3885.
[4] HUANG L, ZHANG J, XU X, et al. Robust adaptive beamforming with a novel interference plus noise covariance matrix reconstruction method[J]. IEEE Transactions on Signal Processing, 2015, 63(7):1643-1650.
[5] CHEN F, SHEN F, SONG J. Robust adaptive beamforming using low complexity correlation coefficient calculation algorithms[J]. Electronics Letters, 2015, 51(6):443-445.
[6] SANTOS E L, ZOLTOWSKI M D. Spatial power spectrum estimation based on a MVDR MMSE MUSIC hybrid beamformer[C].IEEE International Conference on Acoustics, 2005:809-812.
[7] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation, 1986, 34(3):276-280.
[8] LI J, STOICA P, WANG Z. On robust Capon beamforming and diagonal loading [J]. IEEE Transactions on Signal Processing, 2003, 51(7):1702-1715.
[9] JIA W, JIN W, ZHOU S, et al. Robust adaptive beamforming based on a new steering vector estimation algorithm [J]. Signal Processing, 2013, 93(9):2539-2542.
[10] VOROBYOV S, GERSHMAN A B, LUO Z Q. Robust adaptive beamforming using worst case performance optimization: a solution to the signal mismatch problem [J]. IEEE Transactions on Signal Processing, 2003, 51(2):313-324.

