0 引言

    FFT（Fast Fourier Transform）是有限长序列DFT（Discrete Fourier Transform）的一种快速算法，是数字信号处理中的重要工具。工程实践中，根据数据表现形式及中间过程截位规则不同，可将FFT处理器分为3种：定点FFT、块浮点FFT及浮点FFT。相同的FFT算法，在3种运算机制下，计算过程中引入舍入误差不同，输出精度存在明显差异。经研究，FFT算法舍入误差与算法分解级数成正比关系^[1-2]。但舍入误差的引入与运算过程中的截位规则、中间结果范围紧密相连，因此有必要探究不同范围的输入信号、算法相关参数与FFT输出精度的关系，这对实际工程应用改善输出精度、提高噪信比具有重要意义。

1 基4频域抽取FFT算法

    FFT的核心是利用DFT中旋转因子的周期性与对称性，将长序列DFT逐级分解为短序列的DFT，从而减少运算量，提高运算速率^[3-5]。常用FFT包括时域抽取FFT与频域抽取FFT，现介绍工程中广泛应用的一种频域抽取FFT算法，基4频域抽取算法。

    长度为N的x(n)序列DFT变换为：

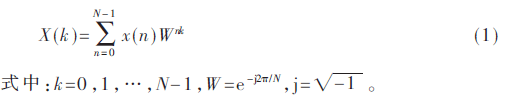
    x(n)按顺序均匀分为4个序列：x(i)，x(i+N/4)，x(i+N/2)，x(i+3N/4)。X(k)则按照除以4所得余数分为4组：X(4r)，X(4r+1)，X(4r+2)，X(4r+3)，i，r=0，1，…，N/4。则基4频域抽取一次分解为：

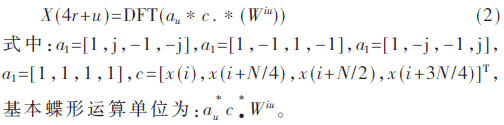
    从式(1)与式(2)对比可以看出，长度为N的长序列进行一次基4 DIF分解，N²次复数乘累加的运算量，降低至N²/4+2N，且包含±j，±1，W⁰等因子的单元可进一步简化运算。长度为N的序列，可进行log₄ N次分解，因此FFT算法大大降低离散傅里叶变换运算量。

2 定点、块浮点、浮点FFT运算过程

    影响FFT输出精度的因素主要包含：系数量化误差，运算过程中舍入误差。本文主要探究运算过程中舍入误差对FFT输出精度的影响。不同运算机制，数据表现形式及输出截位规则有较大差异，引入舍入误差不同，导致最小精度不同。因此有必要对采用定点、块浮点、浮点运算机制时，基4算法运算单元中数据表现形式、输出截位规则、输出最小精度进行分析。

2.1 定点FFT

    定点FFT是输入、旋转因子、输出均为定点形式的一种FFT运算机制。每级蝶形运算，根据输入位宽对运算结果采取高位截取。如图1所示，输入数据位宽为a，旋转因子位宽为b。蝶形输入与因子±j，±1进行乘加运算，幅值全范围位宽扩展至a+2位，与b位有符号旋转因子相乘位宽扩展至a+b+1位，每级蝶形输入位宽要求相同，因此以四舍五入法截取高a位蝶形运算结果进行下级蝶形运算。

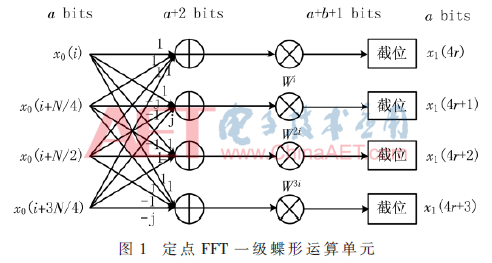
    除去与旋转因子相乘造成的位扩宽，基4定点FFT每级蝶形运算以全范围位宽溢出2位为前提进行舍入。每进行一级蝶形运算，中间结果最小精度扩大4倍。因此，输入序列长度为N时，输出FFT最小精度为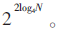定点FFT输出最小精度只与分解级数有关。

2.2 块浮点FFT

    块浮点FFT与定点FFT区别在于对中间截位过程的优化，其结果包含频谱数据及指数。定点FFT默认每级蝶形输出结果均出现符号位溢出，事实上不同量级的输入，中间结果符号位溢出情况是不同的，块浮点FFT通过监测每级蝶形运算输出范围决定截位，从而减少被截取位宽，降低了舍入误差。如图2所示，以正负最大的数值为标准，对每级蝶形输出结果进行截位处理。

    块浮点FFT通过指数表征总体移位结果，输出指数为exp，则最小精度为2^exp，指数由算法输入位宽、输入信号、运算级数共同决定。因此块浮点最小精度与算法输入位宽、信号幅值范围、运算级数相关。

2.3 浮点FFT

    IEEE754标准是1985年IEEE（Institute of Electrical and electronics Engineers，电子电气工程师协会）提出的浮点运算规范，为浮点运算部件工业标准^[6]。IEEE754浮点格式如下：

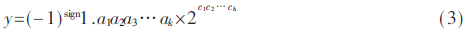
    如式(3)所示，IEEE754浮点格式包含一位符号位，h位无符号偏置指数，k位尾数。数据进行二进制科学计数法表示后，指数部分加上偏置值作为偏置指数，小数部分依次截取k位有效数字作为尾数。如表1所示，IEEE754共提供3种位宽的基础二进制浮点格式。

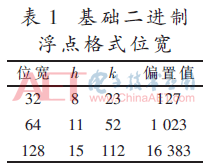
    相同位宽下，浮点格式所表示的数据范围比定点格式大得多。尾数最低位权值为所能表示的最小精度，因此数据越大，浮点表示精度越低。

    浮点FFT输入、输出、旋转因子均为浮点表示形式，涉及的运算均遵循浮点运算准则。计算结果有效位宽溢出导致的舍入误差是浮点FFT主要误差来源。

3 噪信比分析

    为进一步对不同运算机制下FFT计算精度问题进行探索，我们使用输出噪信比表征FFT算法相对误差，研究运算级数、算法输入位宽与输入信号范围与FFT精度的关系。

3.1 浮点FFT噪信比

    浮点FFT误差分析相对困难，文献[1]中提出了基2浮点FFT静态模型，输入为白噪声时，结果如公式(4)所示，噪声与信号均方差比值正比于FFT运算级数v。文献[2]则分析了DIF与DIT以及不同基数下FFT运算下的舍入误差。结果表明，浮点FFT输出噪信比正比于运算级数。

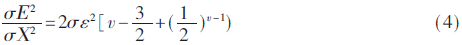
3.2 定点FFT与块浮点FFT仿真模型

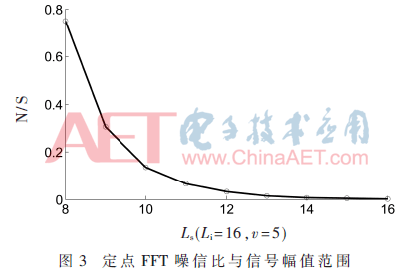
    现于MATLAB平台建立定点与块浮点FFT模型。该模型采用基4频谱抽取算法，输入信号范围、输入位宽与旋转因子位宽可调。计算噪信比N/S=|x_m-x_mat|/|x_mat|，x_m为模型输出，x_mat为MATLAB平台64位浮点计算值。通过仿真，得出输入为随机序列时，输出噪信比与信号全范围位宽Ls、FFT输入位宽Li、运算级数v的关系。

3.2.1 噪信比与输入信号幅值范围关系

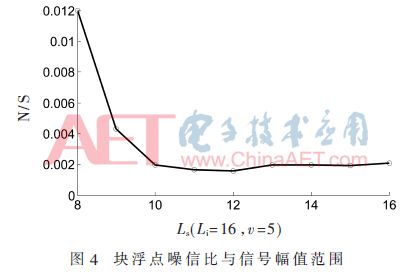
    从图3与图4可以看出，定点FFT噪信比随输入信号范围增大而下降。但对于块浮点FFT，输入信号范围接近输入位宽时，噪信比停止下降，甚至会略有上升。运算级数固定，定点FFT输出最小精度不变。频谱分量大于最小精度时，增大信号输入范围，能够增大频谱分量，有效减小频谱失真率，降低输出噪信比。而块浮点FFT最小精度是随信号频谱分量范围变化的，信号输入范围较小时，块浮点FFT最小精度不变，呈现与定点FFT相同的规律，但随着信号范围增大，最小精度也随着变化，因此噪信比不呈现下降的趋势。

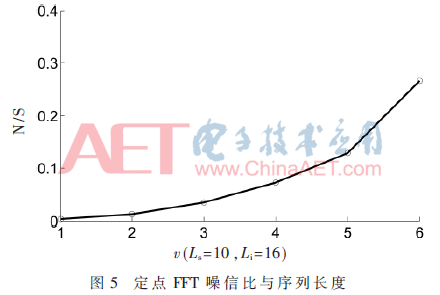
3.2.2 噪信比与输入序列长度关系

    从图5与图6可以看出，无论是定点FFT与块浮点FFT，噪信比都与运算级数近似正比。这是随着运算级数增加，舍入误差线性累积的结果。

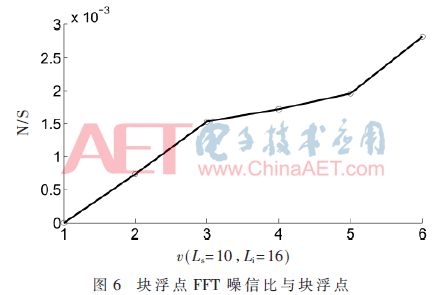
3.2.3 噪信比与FFT输入位宽关系

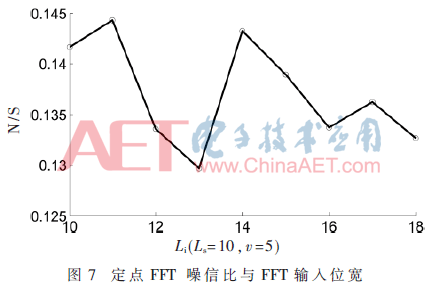
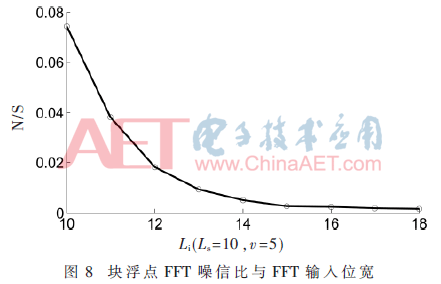
    从图7与图8可以看出，定点FFT输出噪信比与定点FFT输入位宽无关，而块浮点FFT噪信比随着输入位宽增大而减小。这是因为定点FFT，输入位宽并不影响最小精度。而对于块浮点运算机制，FFT输入位宽的增加，降低输出最小精度，输出噪信比降低。

4 小信号FFT精度问题

    实际工程中，使用FPGA进行频谱计算，当输入为白噪声信号时，出现频谱失真的情况，经分析频谱失真与块浮点FFT计算精度有关。

    工程中，对射频接收机输出信号进行采样，经过DDC，不同滤波带宽滤波抽取后，使用块浮点FFT ip核进行FFT计算，FFT输出结果进行位扩展后，依照式(5)进行幅值计算。

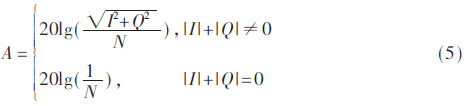
    幅值计算包含对数运算，因此在位扩展之后，将FFT ip核输出实部虚部分量都为0的点幅值固定为常值1，是幅值计算过程基于最小值的数值优化。

    当输入为白噪声情况下，降低信号带宽，出现了图9所示的信号频谱失真。

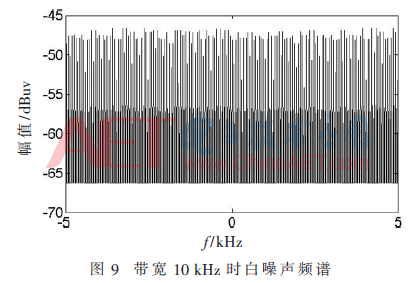
    当滤波带宽较小时，频谱能量小，输出频谱分量小于FFT ip核输出最小精度，因此出现较多零点。

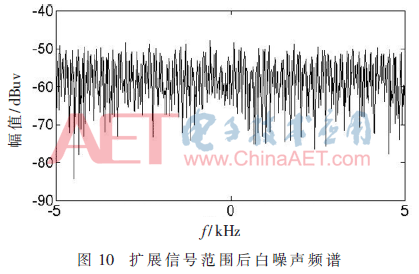
    根据图4所示规律，块浮点FFT运算，当信号范围较小时，噪信比随着输入范围增大而减小。因此可通过扩大输入信号范围来减小噪信比，统一将信号时域分量扩大一定比例值，以使频谱分量大于ip核输出最小精度，减小频谱失真，后续计算环节将比例值抵消后得到新的频谱如图10所示，频谱失真现象得到改善，验证了仿真结论的正确性。

5 结论

    本文通过分析定点、块浮点、浮点机制下，基4算法基本单元运算数据表现形式及截位规则，得出不同运算机制下，FFT舍入误差及输出最小精度。利用仿真模型，得出定点、块浮点FFT噪信比随输入信号范围、FFT输入位宽、序列长度的变化趋势，并基于仿真结论，解决了实际工程中会遇到的小信号频谱失真问题，验证了仿真结果的正确性，对工程师在实际工作中有很强的借鉴性和参考价值。

参考文献

[1] WEINSTEIN C.Roundoff noise in floating point fast Fourier transform computation[J].IEEE Transactions on Audio and Electroacoustics，1969，17(3)：209-215.

[2] THONG T，LIU B.Accumulation of roundoff errors in floating point FFT[J].IEEE Transactions on Circuits and Systems，1977，24(3)：132-143.

[3] COOLEY J W，TUKEY J W.An algorithm for the machine calculation of complex Fourier series[J].Mathematics of computation，1965，19(90)：297-301.

[4] COCHRAN W T，COOLEY J W，FAVIN D L，et al.What is the fast Fourier transform?[J].Proceedings of the IEEE，1967，55(10)：1664-1674.

[5] BRIGHAM E O，BRIGHAM E O.The fast Fourier transform[M].Englewood Cliffs，NJ：Prentice-Hall，1974.

[6] Floating-Point Working Group.IEEE standard for binary floating-point arithmetic[C].SIGPLAN.1987，22：9-25.