0 引言
    VTOL(Vertical Take-Off and Landing)飞行器是能够垂直起降的典型欠驱动系统，因具有对起降环境依赖小、机动性强等特点，被广泛应用于军事和民用领域，其控制研究引发了国内外研究人员的广泛关注[1-3]。VTOL飞行器属于欠驱动系统，具有高度非线性、结构复杂、控制输入受限等特点，这给其控制研究带来了极大的困难[4]。已有大量文献对其进行了深入研究，文献[5]-文献[7]在忽略飞行器滚动控制输入和横向加速度间耦合关系的情况下，采用近似输入-输出线性化方法来研究系统的稳定性以及输出跟踪问题。文献[8]设计了VTOL全局镇定控制律。文献[9]研究了VTOL姿态稳定控制问题。文献[10]在考虑耦合存在的前提下，采用李雅普诺夫直接法设计了飞行器渐近稳定跟踪参考轨迹的控制器。
    目前，VTOL飞行器的跟踪问题仍然是控制领域的研究热点。作为一种具有完全鲁棒性的变结构控制方法，滑模控制具有响应迅速、对系统参数变化和外界扰动不敏感、无需系统在线辨识、物理实现简单等优点[11]。因此可以用来控制VTOL飞行器。
    本文对具有3个自由度、2个控制输入的VTOL飞行器的输出跟踪问题进行了研究，提出了一种分层滑模控制方案，可以实现飞行器在考虑输入耦合情况下的轨迹跟踪。
1 VTOL飞行器动力学模型
    根据文献[5]，VTOL飞行器动力学模型表示为：

2 分层滑模控制器设计
    本文解决的是欠驱动系统的输出跟踪问题，模型有3个输出、2个输入，对于跟踪问题，只能保证位置信号跟踪指令，定义飞行器的横、纵坐标的期望轨迹指令为x_1d和y_1d，控制目标为：系统(1)的x₁和y₁跟踪指令信号x_1d和y_1d，滚转角θ镇定。通过对系统(2)的控制律进行设计，可以完成控制目标。定义z₁、z₂、z₃、z₄的跟踪指令信号分别为z_1d、z_2d、z_3d、z_4d，跟踪误差为：e₁=z₁-z_1d，e₂=z₂-z_2d，e₃=z₃-z_3d，e₄=z₄-z_4d，则有。
    对于给定的指令信号z_1d、z_2d、z_3d、z_4d，通过设计合适的控制律h使得e₁→0，e₂→0，e₃→0，e₄→0，系统就能够完成跟踪任务。
    对两个子系统分别定义滑模面：
    s₁=c₁e₁+e₂， s₂=c₂ e₃+e₄                       (5)
其中c1>0，c2>0。
    构造系统的总滑模面为：
    S=c₂(e₃-z)+e₄                                      (6)
    这里z为中间变量，是s1的函数，定义为：

3 系统稳定性分析
    本节用Lyapunov稳定性定理、Barbalat引理分别证明了各个滑模面的稳定性及误差子系统的渐近稳定性。
    Barbalat引理^[12]：如果，则。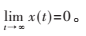
3.1 系统总滑模面稳定性
    定理1 对于系统(2)，按式(5)和式(6)构造系统的滑模面，采用控制律式(13)，则系统的总滑模面S是渐近稳定的。

3.2 子系统滑模面稳定性
    定理2 对于系统(2)，按式(5)和式(6)构造系统的滑模面，采用控制律(13)，则两个子系统的滑模面s1和s2是渐近稳定的。
    证明：定义中间变量：
  

4 仿真结果
   

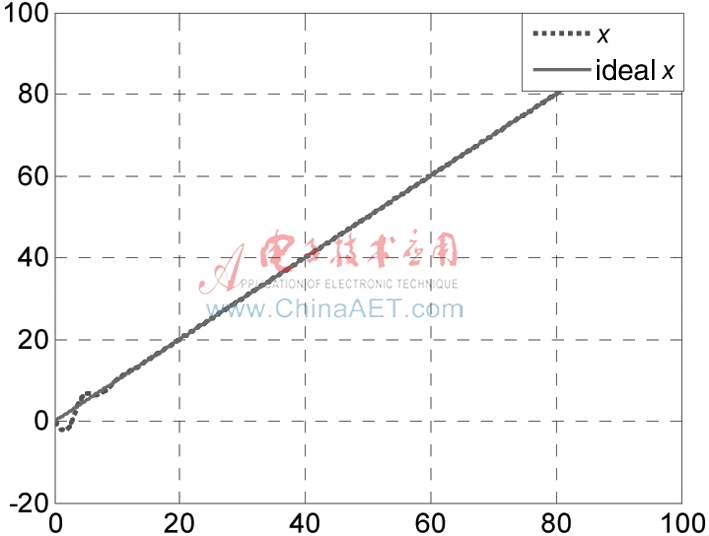
图1  飞行器质心的位置x1(t)跟踪

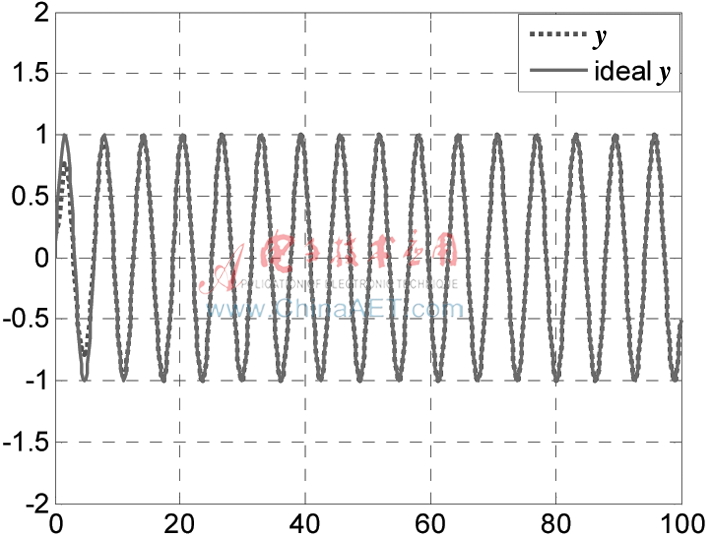
图2  飞行器质心的位置y1(t)跟踪

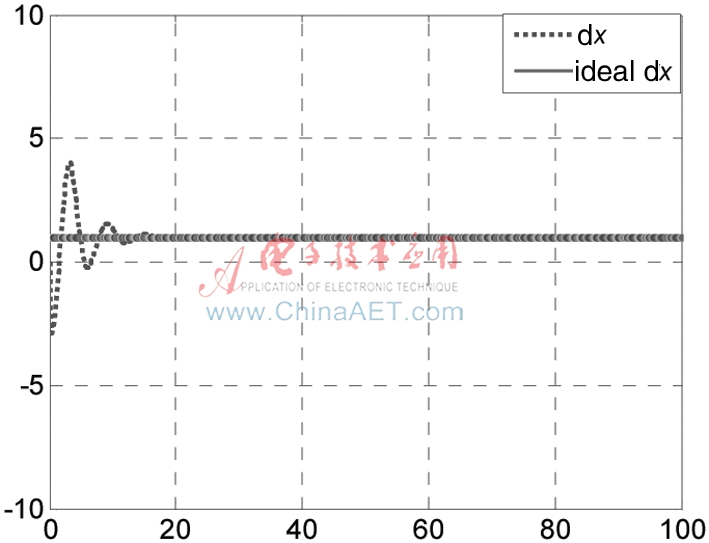
图3  飞行器质心的速度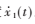跟踪

图4  飞行器质心的速度跟踪

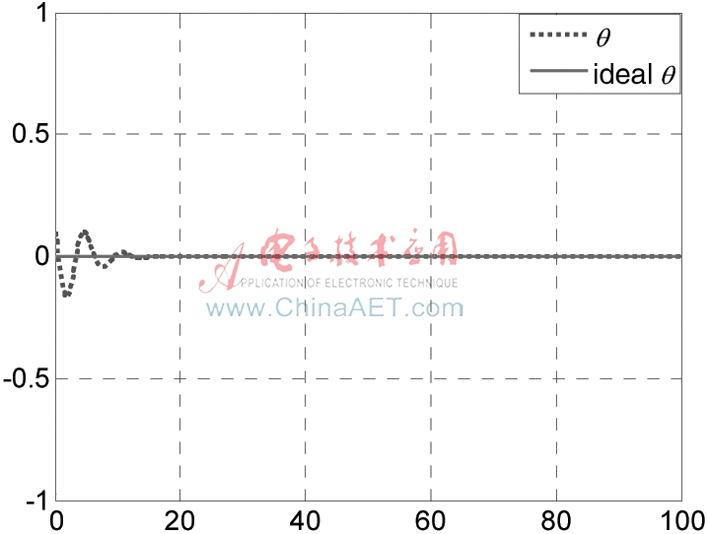
图5  飞行器滚动角度θ(t)的镇定

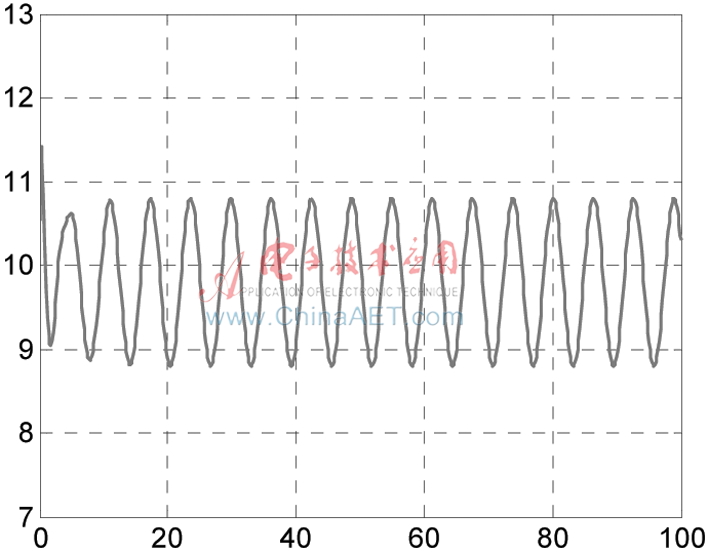
图6  飞行器底部推力控制输入u₁

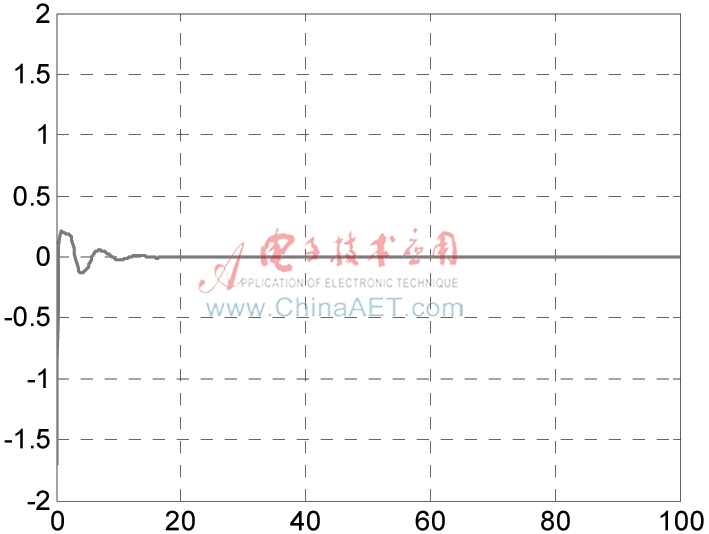
图7  飞行器滚动控制输入u₂

    图1～图2表明，在控制器作用下，飞行器实际位置轨迹快速、稳定地收敛于期望位置轨迹。由图3～图4可见，飞行器实际速度轨迹快速、稳定地收敛于期望速度轨迹。图5表明，滚转角快速收敛到?兹=0。图6和图7为控制输入曲线，可以看出控制器快速、平稳地渐近收敛，控制效果很好。仿真结果验证了所提出的滑模控制器的有效性及前面给出的稳定性分析的正确性。
5 结论
    对于VTOL飞行器的输出跟踪问题，本文提出了一种分层滑模控制方案，可以实现飞行器在考虑输入耦合情况下的轨迹跟踪，并利用李亚普诺夫稳定性理论和Barbalat引理详细证明了各个滑模面的渐近稳定性和误差系统的全局渐近稳定性。与已有的控制方法相比，该方法提出的控制器设计简单、响应速度快，对系统参数变化和外界干扰具有鲁棒性，能够实现对给定轨迹的渐近稳定跟踪。同时，给出的仿真结果进一步验证了这种滑模控制方法的有效性和可行性。
参考文献
[1] WANG X H，LIU J K，CAI K Y.Tracking control for a velocity-sensorless VTOL aircraft with delayed outputs[J].Automatica，2009，45(12)：2876-2882.
[2] ROBERTS A，TAYEBI A.A new position regulation strategy for VTOL UAVs using IMU and GPS measurements[J].Automatica，2013，49(2)：434-440.
[3] ABDESSAMEUD  A，TAYEBI A.Global trajectory tracking control of VTOL UAVs without linear velocity measurement[J].Automatica，2010，46(6)：1053-1059.
[4] ROBERTS A，TAYEBI A.Adaptive  position  tracking  of  VTOL UAVs[J].IEEE Transactions on Robotics，2011，27(1)：129-142.
[5] HAUSER J，SASTRY S，MEYER G.Nonlinear control design for slightly non-minimum phase systems[J].Automatica (S0005-1098)，1992，28(4)：665-679.
[6] MARTIN P,DEVASIA S,PADEN B.A different look at output tracking：control of a VTOL aircraft[J].Automatica(S0005-1098)，1996，32(1)：101-107.
[7] HUANG C S，YUAN K.Output tracking of a non-linear non-minimum phase PVTOL aircraft based on non-linear state feedback[J].International Journal of Control(S0020-7179)，2002，75(6)：466-473.
[8] OLFATI-SABER R.Global configuration for the VTOL aircraft with strong input coupling[J].IEEE Transactions on Automatic Control(S0018-9286)，2002，47(11)：1949-1952.
[9] TAYEBI A，MCGILVRAY S,Attitude stabilization of a VTOL quadrotor aircraft[J].IEEE Trans.Control Systems Technology，2006，14(3)：562-571.
[10] DO K D，JIANG Z P，PAN J.On global tracking control of a VTOL aircraft without velocity measurements[J].IEEE Transactions on Automatic Control(S0018-9286)，2003，48 (12)：2212-2217.
[11] HUNG J Y，GAO W，HUNG J C.Variable structure control：a survey[J].IEEE Transactions on Industrial Electronics，1993，40(1)：2-22.
[12] TAO G.A simple alternative to the barbalat lemma[J].IEEE Transactions on Automatic Control，1997，42(5)：698.