人工地震勘探是指利用现有的技术(如各类传感器)接收来自不同深度及距离的震源产生的震动波。人工地震勘探依照传感器与震源距离及震源深度的不同，一般分为4种类型:小区域浅层(深度一般不超过100 m)地下震动探测、小区域深层地下震动探测、大范围浅层地下震动探测、大范围深层地下震动探测。受传输介质本身密度的不均匀及弹性模量差异的影响，不同种类地震勘探所获取的震动信号分别具有各自不同的特点。对这些震动信号进行处理和分析对于工程爆破，炸点、震源定位等具有十分重要的意义。震动波的类型一般包括瑞雷面波、勒夫波、横波及纵波，以波速及传播方向的不同作为这4类波的区分标准。在实际测量中，由于周围环境的干扰，实测震动信号一定混有噪声，直接对其进行时频分析难度较大并且处理后的信号波形也不是十分理想，因此，对实测震动混合信号进行降噪处理及不同种类波的分离是首先需要解决的问题。为此，本文提出将盲源分离[1-2]理论应用于混合信号的信噪分离及震动信号中各种波的分离。

1 基于时间延迟的盲源分离算法原理

　　在混合震动信号中,不同种类的波是线性混合的，但信号与噪声的混合方式却是非线性的。因此,提出一种快速有效的既适用于线性混合信号又适用于非线性的盲源分离算法对于震动信号预处理具有十分重大的意义。

　　1.1 数据分析

　　通常地震勘探所采用传感器采集到的数据都是间隔一定的采样时间所对应的电压幅值。将采样时间作为横轴，电压幅值作为纵轴，就得到了震动信号的波形图，即时间序列波形数据。

　　将传感器采集到的电压幅值数据看做是一个1行p列(采样点数)的矩阵。则将所得到的n组数据组成一个新的矩阵x(n×p阶的矩阵),其中n为观测信号个数,p为采样点数。

　　1.2 算法原理

　　无论是线性或者非线性盲源分离[3-4]算法，最终就是求得解混矩阵[5]w从而达到实现信号分离目的。首先必须明确的是式(1)中给出的约束最小化损失函数模型：

　　其中,G′是函数G的导数，F′为F的导数。式(2)中，对于权重w的更新算式(3)所示：

　　由式(3)可知，函数G的确切形式对求取解混矩阵w并不起决定性的作用，而功能函数F的选择则直接影响w的数值及最终的分离结果。在此提出一种z变换域有理传递函数:

　　1.3 算法实现的具体步骤

　　(1)对观测到的混合震动信号x(t)n×p进行归一化处理，得到新矩阵(t)n×p中的各分量互不相关且其每个元素均是归一化的单位方差。

　　(2)求步骤(1)中得到的归一化矩阵T(t)的自协方差矩阵Un×n。

　　(3)求步骤(2)中得到的自协方差矩阵的特征向量及特征值矩阵Fn×n和Dn×n(对角元素为特征值，其他元素均为零)，使得矩阵U、F和D满足式(5)：

　　U·F=F·D  (5)

　　(4)求矩阵D的对角矩阵n×n(D矩阵各对角元素的二次方根取倒数并保留实部后，按照大小顺序降序排列)。

　　(5)由步骤(3)中的矩阵F和步骤(4)中的矩阵求得白化矩阵vn×n，使得三者满足如下关系式：

　　(7)设定合适的时间延迟?子(一般情况下，10≤≤100)根据采样点数p的大小选择合适的滞后常数值。

　　(8)生成矩阵a1×，令其所有元素值均为1/。

　　(9)将步骤(6)中得到的矩阵xT(t)和步骤(8)中生成的矩阵a带入式(3)，得到矩阵gp×n。

　　(10)求步骤(9)中得到的矩阵g的自协方差矩阵Vn×n。

　　(11)利用步骤(2)中得到的矩阵U和步骤(10)中得到的矩阵V，求得广义特征对角矩阵Qn×n和解混矩阵wn×n(全矩阵)，使U、V、Q和w满足：

　　V·w=U·w·Q (8)

　　(12)由式(9)解出估计信号矩阵y(t)n×p:

　　yT(t)=xT(t)·w  (9)

2 算法仿真

　　2.1 仿真信号的生成

　　利用Matlab产生的震动仿真信号验证上诉算法的可行性及有效性。分离过程的系统框图如图1所示。

　　以小区域浅层地下震动仿真信号为例，由于传感器距震源较近，其接收到的震动信号可以近似认为只含有横波及纵波，并且二者以线性方式混合。通过正弦波与衰减型指数函数叠加并进行数次迭代即可得到横、纵波的仿真波形，二者差别主要在于正弦波幅值、指数函数的基和初至时间的设置上。

　　生成长度L=10 000的横、纵波波形如图2所示。图2中横轴时间的取值考虑到是以小区域浅层地下震动为仿真背景，布阵传感器与震源相距较远，传感器接收到震动信号的时间大约在震源起振66 s以后。二者叠加后的合成震动信号s_s如图3(a)所示。

　　其次就是噪声与合成震动信号的非线性叠加，仿真过程中需选取较切合实际情况的强非线性叠加方式。Matlab产生有色噪声波形如图3(b)所示。

　　有色噪声与合成震动信号以式(10)~式(13)的形式进行强非线性混合，得到混合信号m_s1、m_s2、m_s3、m_s4的波形如图4所示。

　　m_s1=tanh(s_s)+2tanh(c_n)  (10)

　　m_s2=tanh(c_s)+2tanh(s_n)  (11)

　　m_s3=s_s.^3+2c_n.^3  (12)

　　m_s4=c_s.^3+2s_n.^3  (13)

　　2.2 信噪分离

　　由于本文应用正定盲源分离算法，所以分离出的信号应该也是4路。但是由于并不关心噪声信号，所以图5只给出分离出的2路震动信号的波形，并没有给出噪声波形。

　　2.3 横、纵波分离

　　虽然盲源分离算法分离出的信号顺序不确定，但是从初至时刻的前后可以判断出横、纵波。从图6中可以看出，由于分离出的信号还含有一定的噪声，所以波形会出现毛刺现象。

3 仿真结果与分析

　　3.1 分离效果的评价标准

　　3.1.1 二次残差(VQM)

　　该分离指标利用估计信号yi(t)在源信号xi(t)上的投影来计算信噪比，计算公式为:

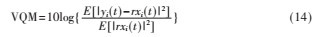
　　其中r=E[yi(t)xi(t)]/E[xi2(t)]。由该式计算出信噪分离后的震动信号的VQM≈13 dB。

　　3.1.2 相似系数(?着)

　　为了评价分离效果,采用分离信号与原信号的相似系数?着作为分离的性能指标:

　　设xi(t)为源信号矢量x(t)中的第i(本文中，1≤i≤4)个信号，yi(t)为经过盲抽取后的与xi(t)相对应的分离信号，则yi(t)与xi(t)之间的相似系数为:

　　当||=1时，表示yi与xi完全相似；当|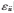|≥0.9时，认为该算法还原效果较理想。

　　3.2 仿真结果

　　各波形的相似度结果如表1所示。

　　该算法的各个程序运行时间如表2所示。

　　本文提出了一种盲源分离优化算法，既适用于分离以线性方式混合的信号,也适用于以非线性方式混合的信号。同时,提出将盲源分离算法应用于一个新的领域，即对震动信号的预处理。本文中主要针对震动信号进行信噪分离及横、纵波分离，该结果对信号后期的时频分析等具有十分重要的意义。

参考文献

　　[1] 李小军，朱孝龙，张贤达.盲信号分离研究分类与展望[J].西安电子科技大学学报，2004，31(3)：399-404.

　　[2] 刘富凯，张家润.基于盲源分离技术的自适应电力谐波检测算法研究[J].电子技术应用，2012，31(22)：67-70.

　　[3] CICHOCKI A，GEORGIEV P.Blind source separation algo-rithms with matrix constrains[J]. IEICE Transactions on In-formation and Systems，2003，E86-A(3)：522-531.

　　[4] CHEUNG Y M，LIU H L. A new approach to blind sourceseparation with global optimal property[C]. Proceedings ofthe IASTED Iternational Conference of Neural Networks andComputational Intelligence, Griedelwald，Switzerland，2004：137-141.

　　[5] YILMAZ O,RICKARD S. Blind Separation of Speech Mix-tures via Time-Frequency Masking[J].IEEE Transactions onSignal Processing,2004,52(7):1830-1847.