文献标识码: A
文章编号: 0258-7998(2014)08-0072-04
遥操作穿刺手术是通过专用手术器械插入患者体内,并在医学图像的引导下,对患者体内的病灶进行手术操作的外科手术。穿刺手术具有创伤小、痛苦小、康复快、术后并发症少等优点,是当前主要发达国家竞相研究的医学领域之一[1]。目前已有很多较为成熟的医疗遥操作系统,如美国的Computer Motion公司研发的AESOP腹腔镜操作机器人[2]、Zeus微创手术机器人系统[3]以及Intuitive Surgical公司研发的Da Vinci微创手术机器人系统[4]等具有代表性的医疗遥操作系统。它们不仅为医生提供了先进的视觉反馈,而且让手术医生拥有了更加灵活的操作方式,使得手术过程变得相对简单和容易完成,在医疗手术机器人领域具有革命性的意义。
本文主要在遥操作系统已有主从控制的基础上,针对施加在主机器人的主动约束进行了相关半实物仿真研究,从而能够实现主从控制中的虚拟向导功能,并获得较好的控制精度、响应速度和安全性。
1 主从机器人构型
本文系统采用主从式控制结构,外科医生通过操纵主机器人(主手)来实现对从机器人(从手)的控制,从而完成相关手术任务。本系统的主手采用SensAble公司生产的Phantom Omni[5],具有6自由度(DOF),所有关节均为旋转关节,前三个关节控制机器人末端位置坐标,后三关节采用三轴交汇于一点,用于控制机器人姿态坐标。
从机器人作为手术系统的执行部分负责完成手术操作,拥有6DOF,且都是旋转关节,前三个关节配合实现末端定位;后三个关节采用三轴交汇的形式实现末端姿态的调整。
2 虚拟夹具算法
VF是一种基于软件的主动约束模型,通过产生的虚拟力来限制机器人朝禁止区域运动或引导机器人沿理想路径运动[6-8]。VF一般分为引导型VF(guidance virtual fixture,GVF)和禁止型VF(forbidden virtual fixture,FRVF),本文主要研究在主手端的线型和面型VF。
2.1 线型VF
在线型VF算法计算中,首先需要计算机器人末端目标位置与实际位置的偏差,表示为:
Xd-X0=(Xm-X0)·v (1)
其中,Xd表示主手末端目标位置,Xd=[xd,yd,zd]T;X0表示理想直线的初始点,X0=[x0,y0,z0]T;v表示理想直线的单位方向向量;Xm表示主手末端实际位置,Xm=[xm,ym,zm]T。
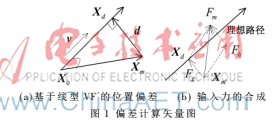
偏差计算矢量图如图1所示。根据向量运算法则,由式(1)可得主手位置偏差公式:
![3BK4S]O$~EB~X)T4@{ZTQ`K.png 3BK4S]O$~EB~X)T4@{ZTQ`K.png](http://files.chinaaet.com/images/2017/01/25/6362094652682200005297501.png)
然后,再利用VF算法来计算虚拟向导力,此虚拟向导力迫使机器人朝着偏差减小的方向运动。如图1(b)所示,输入到主机器人的输入力Fm为虚拟向导力Fg与操作者输入力Fh的合成力,表示为:
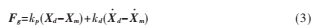
其中,kp和kd分别表示弹性系统和阻尼系数。
本系统的最大偏差值设定为dmax=3 mm,当机器人末端位置偏差不小于此值时虚拟向导力都取最大值Fg=3 N。
2.2 面型VF
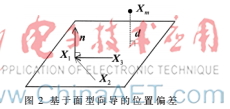
在面型VF算法中,由于位置偏差为机器人末端Xm到约束平面上的投影点Xd的距离,也即机器人末端到约束平面的距离,所以该位置偏差可以直接根据机器人末端到约束平面的距离来计算。如图2所示,给定约束平面上的任意三点X1、X2和X3,从而可以得到约束平面上的两个矢量v1和v2以及约束平面的法向量n,表示为如下表达式。
v1=X1-X2 (4)
v2=X1-X3 (5)
n=v1×v2 (6)
由以上三式联立,可得到约束平面的标准表达式:
(X-v1)n=Ax+By+Cz+D=0 (7)
其中,A=n1,B=n2,C=n3,D=-(n1v11+n2v12+n3v13)。
利用以上表达式可以计算机器人末端位置Xm到达平面的距离,也即机器人末端到约束平面的偏差d为:

通过上式可以得到位置偏差矢量的表达式为:
d=‖n‖d (9)
主手末端越靠近约束平面其受到的虚拟向导力越大,此虚拟向导力可以是排斥力也可以是吸引力,这个虚拟向导力同样利用弹簧-阻尼模型建模。
2.3 基于面型VF的Proxy方法

本文提出基于软件的一个虚拟点(Proxy)的概念,Proxy通过弹簧模型虚拟地连接到主手末端[9]。如图3所示,设定一个平行于yz平面的约束平面x=a(a为已知常量),平面左侧为机器人工作空间下的自由运动区域,平面右侧为工作空间下的禁止运动区域。当主机器人末端在x=a平面左侧时,主机器人直接控制从机器人;当主机器人末端在平面x=a平面右侧时,Proxy取代主机器人控制从机器人,此时Proxy就是主机器人末端在约束面上的投影点Xd,用数学表达式描述如下:
![YXJGZIV6X]062H1OV(N]W0S.png YXJGZIV6X]062H1OV(N]W0S.png](http://files.chinaaet.com/images/2017/01/25/6362094661028400007209159.png)
其中Xproxy表示Proxy的位置,Xm表示主机器人末端位置,Xd表示主机器人末端在约束面上的投影点位置。
综上所述,可得到基于面型VF的Proxy方法具体实现步骤如下:
(1) 当主手末端在约束平面x=a左侧时,也即主机器人末端在X轴的值xm<a时:
(a)主手末端越靠近约束平面,末端受到来自约束面的虚拟排斥力Fg就越大,表示为:

其中,kp1为弹性系数。
(b)此时Xproxy=Xm,也即是从手跟随主手运动。
(2)当主手末端在约束平面x=a右侧时,也即xm≥a时:
(a)主手末端距离约束平面越远,其末端受到来自Proxy
的虚拟吸引力Fg也越大,表示为:
Fg=kp2(Xd-Xm) (12)
其中,kp2为弹性系数。
(b)此时Xproxy=Xd,即从手跟随Proxy运动。
3 半实物仿真
为了验证本文方法的有效性,利用上述主从控制方案分别进行主从跟随的半实物仿真实验。本半实物仿真实验是在带有Phantom 工具箱[10]的MATLAB Simulink实时仿真环境下进行的。
3.1基于主从控制的线型VF仿真
在半实物仿真过程中,首先定义主手在工作空间中的两个点,分别表示为直线的起点和该直线上的任意一点,该直线被称为主机器人的理想运动路径,也即是理想情况下,主手末端将沿该直线运动。当主手末端位置偏离该理想路径时,通过VF产生虚拟向导力会将其拉回到理想运动路径上来。如图4所示,为半实物仿真结果。
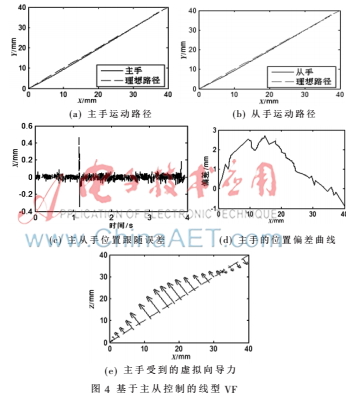
图4(a)、(b)分别表示主、从手末端位置在xy平面下的运动轨迹,从图中可以看出主从手末端基本能够满足沿理想路径的运动。图4(c)表示主从跟随在X轴的误差,其最大误差值为|ex|=0.51 mm,在Y、Z轴上的最大误差分别为|ex|=0.46 mm、|ex|=0.49 mm。图4(d)、(e)分别表示主手末端沿理想路径运动时的偏差及其对应的虚拟向导力,从图中可以看出随着运动偏差的增大,其对应的虚拟向导力也会对应增大,反之亦然,其中在X轴的最大偏差为2.83 mm时对应的最大虚拟力|fx|=1.97 N。本仿真验证了线型VF算法的正确性。
3.2 基于主从控制的面型VF与Proxy仿真
首先定义主手在工作空间中约束平面及禁止区域,为方便起见,本系统定义约束平面为x=45 mm,并指定约束面右侧为禁止区域。图5所示为半实物仿真结果。
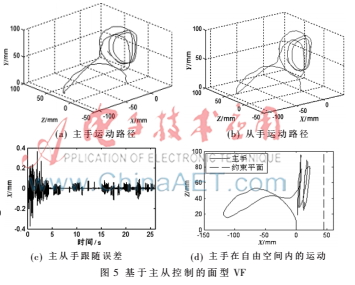
图5(a)、(b)分别表示主从手在坐标平面YZ上的运动;图5(c)表示主从跟随运动在X轴的误差,其最大误差为|ex|=0.38 mm,且在Y、Z轴的最大误差分别为|ex|=0.37 mm、|ex|=0.34 mm,基本能够满足主从跟随的精度要求。图4(d)表示主手在平面XZ上的运动,机器人末端在X轴方向越靠近约束面时受到的虚拟向导力(排斥力)越大,当主手末端距离小于等于33.32 mm时,其受到的排斥力达到最大值fgx=3 N。
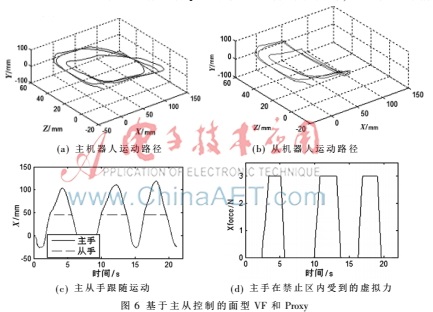
图6所示为主手末端穿越其约束面达到其右侧(也即进入到禁止区域)时的运动。在此假定主手末端在约束面左侧(也即自由运动区域)运动时,不受虚拟向导力的作用。
图6(a)、(b)分别表示主、从机器人的运动。从图6(c)可以看出,当主手末端在约束面右侧运动时,从手能够跟随主手运动;当主手末端穿越约束面,在其右侧运动时,从手就会脱离主手而跟随Proxy运动,并且Proxy在约束面(x=45)上跟随主手运动, Proxy在X轴的值就保持在xproxy=45 mm,Proxy在Y、Z轴的坐标跟随主手末端坐标实时变化。图6(d)表示主手末端穿越约束面后,在禁止区域的受力情况。比较图6(c)、(d)可以看出,当主手末端在约束面左侧时其受到的作用力为0 N,可以自由运动;当其进入到禁止区域后,与Proxy的距离偏差越大其受到来自Proxy的虚拟向导力(吸引力)也越大,当该偏差大于等于30.04 mm时,吸引力达到最大值fgx=3 N,迫使主手末端返回自由运动区域。本仿真验证了面型VF算法结合Proxy方法的正确性。
综上所述,基于主从控制的线型VF和面型VF的半实物仿真实验基本实现了预期的功能,性能基本符合预期的工作目标。系统安全性得到了提高,当出现意外情况时不致出现危险或误操作,保证了手术的精确性与安全性。
为了满足穿刺手术机器人主从运动控制的精确、快速以及安全性,本文提出了基于主从控制的主动约束控制策略。半实物仿真结果验证了算法的可行性,基本能够满足穿刺手术任务的要求。本文研究只涉及运动学方面,而没有涉及动力学方面的研究,下一步工作是通过动力学方面的研究来进一步完善本系统。
参考文献
[1] KAZANZIDES P, FICHTINGER G, HAGER G D, et a1.Surgical and interventional robotics-core concepts,technolo-gy, and design[J]. IEEE Robotics and Automation Maga-zine, 2008, 15(2): 122-130.
[2] SHEW S B, OSTLIE D J, HOLCOMB G W. Robotic tele-scopic assistance in pediatric laparoscopic surgery[J]. Pedi-atric Endosurgery and Innovative Techniques, 2003,7(4):371-376.
[3] LANFRANCO A R, CASTELLANOS A E, DESAI J P, etal. Robotic surgery-a current perspective[J]. Annals ofSurgery, 2004, 239(1): 14-21.
[4] BROEDERS I, RUURDA J. Robotics revolutionizing surg-ery: The intuitive surgical “Da Vinci” system [J]. Indus-trial Robot, 2001, 28(5): 387-391.
[5] SILVA A J, RAMIREZ O A D, OLIVER J P O. PHAN-ToM OMNI haptic device: kinematic and manipulability[C].Robotics and Automotive Mechanics Conference, 2009:193-198.
[6] ALIAGA I, RUBIO I, S?魣NCHEZ J. Experimental quantita-tive comparison of different control architectures for master-slave teleoperation[J]. IEEE Transactions on Control Sys-tems Technology, 2004,12(1):2-11.
[7] 谢琦,潘博,付宜利等.基于腹腔微创手术机器人的主从控制技术研究[J].机器人,2011,33(1):53-58.
[8] PARK S, et al. Virtual fixtures for robotic cardiac surgery[C].In Proc.4Th Int’l. Conf. on Medical Image Computing andComputer-Assisted Intervention,2001:1419-1420.
[9] BOWYER S A, DAVIES B L, BAENA F R. Active con-straints/virtual fixtures: a survey[J]. IEEE Transactions onrobotics, 2013,9(19).
[10] MOHAMMADI A, TACAKOLI M, JAZAYERI A. PHAN-TSIM:A simulink toolkit for the sensable PHANToM Hap-tic Devices[C].Proceedings of the 23rd CANCAM, Canada.2011:787-790.

