文献标识码: A
文章编号: 0258-7998(2014)08-0105-04
非协作通信中符号率盲估计是正确解调的前提,常用符号率盲估计方法主要有小波分析法[1]、循环谱法[2]及最大似然法[3]等。黄春林[4]利用循环谱对符号率进行估计,信噪比在0 dB时均方根误差在8.5%,计算量过大;金艳[2,5]对基于循环自相关方法进行改进,减小了计算量,并给出了提高信噪比的方法,但受限于精确延迟选取困难,无法实际应用。本文针对PSK信号,将功率谱累加及拐点搜索逼近符号率粗估计算法与改进的循环谱符号率精估计算法相结合,提出了一种速率符号率估计新方法,降低计算量的同时提高了抗噪性。
1 循环谱估计
x(t)为一循环平稳随机过程,自相关函数为:
![]978Z7P1JQV{J@)@`PW3AEV.png ]978Z7P1JQV{J@)@`PW3AEV.png](http://files.chinaaet.com/images/2017/01/25/6362095915688200002053815.png)
其中,![F}VHK2~{5DX6$HZ7HD]GTAU.jpg F}VHK2~{5DX6$HZ7HD]GTAU.jpg](http://files.chinaaet.com/images/2017/01/25/6362095950678700006545249.jpg) =k/T为循环频率,k为整数。
=k/T为循环频率,k为整数。![_N~NV3RWO~LCU]8V[PQ3~GG.jpg _N~NV3RWO~LCU]8V[PQ3~GG.jpg](http://files.chinaaet.com/images/2017/01/25/6362095951017800004717976.jpg) 的傅里叶变换
的傅里叶变换 称为周期谱密度函数[6]:
称为周期谱密度函数[6]:

Rx?琢(?子)可以看成x(t)的两个复数频移函数U(t)和V(t)的互相关:
![QZ699(KHA2F)~JKPRKSH]7J.png QZ699(KHA2F)~JKPRKSH]7J.png](http://files.chinaaet.com/images/2017/01/25/6362095957924400007857191.png)
因此,![_N~NV3RWO~LCU]8V[PQ3~GG.jpg _N~NV3RWO~LCU]8V[PQ3~GG.jpg](http://files.chinaaet.com/images/2017/01/25/6362095959840200004675800.jpg) 是U(t)和V(t)互谱密度函数SUV(f)的傅里叶反变换,有:
是U(t)和V(t)互谱密度函数SUV(f)的傅里叶反变换,有:
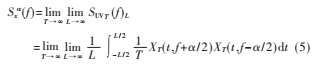
其中,XT(t,f)为x(t)的短时傅里叶变换,Sx![F}VHK2~{5DX6$HZ7HD]GTAU.jpg F}VHK2~{5DX6$HZ7HD]GTAU.jpg](http://files.chinaaet.com/images/2017/01/25/6362095961099900006969136.jpg) (f)称为谱相关密度函数,L为平滑窗长度。PSK信号谱相关密度函数为:
(f)称为谱相关密度函数,L为平滑窗长度。PSK信号谱相关密度函数为:
BPSK时:
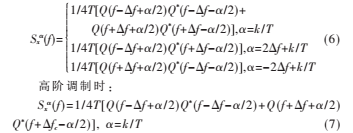
其中Q(f)=sin(![F}VHK2~{5DX6$HZ7HD]GTAU.jpg F}VHK2~{5DX6$HZ7HD]GTAU.jpg](http://files.chinaaet.com/images/2017/01/25/6362095963825200007855446.jpg) fT)/(fT)。对式(6)、式(7)进行二维搜索可得到PSK符号率估计值,但计算量大且低信噪比时估计性能差。参考文献[2]运用一维切片搜索仅仅降低了部分计算量,参考文献[5]提出符号率估计精度与噪声功率和观测数据长度有关,可通过降噪和增加观测数据长度来提高估计精度,算法本身没有改进。
fT)/(fT)。对式(6)、式(7)进行二维搜索可得到PSK符号率估计值,但计算量大且低信噪比时估计性能差。参考文献[2]运用一维切片搜索仅仅降低了部分计算量,参考文献[5]提出符号率估计精度与噪声功率和观测数据长度有关,可通过降噪和增加观测数据长度来提高估计精度,算法本身没有改进。
2 盲估计改进算法
2.1 符号率粗估计
Xk为离散信号x(k)的傅里叶变换系数,Xk2表示信号功率谱,包含码速率信息。对序列Xk2进行长度为m的累加,得到Xk的平方和累加序列Yk:
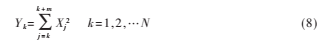
采样频率fs=512 MHz、符号率R=32.704 Mb/s、滚降因子![F}VHK2~{5DX6$HZ7HD]GTAU.jpg F}VHK2~{5DX6$HZ7HD]GTAU.jpg](http://files.chinaaet.com/images/2017/01/25/6362096028454800007931849.jpg) =0.4、SNR=-5 dB、FFT长度M=8 192、累加长度m=300时,BPSK信号功率谱Xk2累加序列Yk如图1所示。序列Yk关于中心频率大致对称,因此通过搜索功率谱拐点处频点festi即可得到符号率粗估计值。
=0.4、SNR=-5 dB、FFT长度M=8 192、累加长度m=300时,BPSK信号功率谱Xk2累加序列Yk如图1所示。序列Yk关于中心频率大致对称,因此通过搜索功率谱拐点处频点festi即可得到符号率粗估计值。
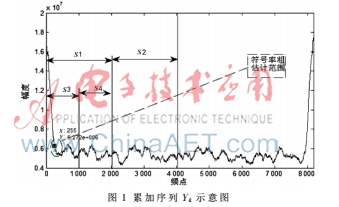

功率谱拐点处频点festi逼近搜索算法:起始频点f0=M/4,以f0为中心计算S1和S2范围内样点幅度平均值A1和A2,再将S1区域平分为S3和S4,计算平均值A3和A4。若(A1-A2)>(A3-A4),则重复上述步骤向左搜索,否则向右搜索,循环搜索8次,求得符号率粗估计值。
累加长度m既决定了准确率也对运算量有非常大的影响。序列Yk为能量累加结果,表示FFT变换后系数自相关(延迟为0)函数累加。理论上m越大越好,但随m增大计算量迅速增大。表1所示为R∈[25 Mb/s,128 Mb/s]以128 kb/s步进时累加长度m对粗估计正确率的影响。

估计值在[2R/3,3R/2]范围内视为正确,由表1可知累加长度m越大粗估计正确率越高,-5 dB、m=256时准确率已达99.8%,而当m=320时准确率为100%。
2.2 循环谱估计改进算法
在高信噪比时通过式(6)、式(7)可以准确地完成符号率估计,基-2FFT时间抽取算法如式:
X(k)=X1(k)+WNkX2(k) k=0,1,…,N/2-1 (10)
X(k+N/2)=X1(k)-WNkX2(k) k=0,1,…,N/2-1 (11)
其中,X(k)为信号x(t) N点FFT前半部分,X(k+N/2)为信号x(t) N点FFT后半部分,两部分相似,相关度高。为充分利用该相似性,将式(5)表示为:
![PDTKC@GH947TT()]61~8_WU.png PDTKC@GH947TT()]61~8_WU.png](http://files.chinaaet.com/images/2017/01/25/6362095971144200001914873.png)
其中X(k+L-n),X′(N-k-n)分别表示x(k) FFT变换前半部和后半部。由式(12)进行全域搜索即可得到符号率完成精估计。相比式(7),循环谱计算量减小一半,且通过互相关能够抑制噪声,提高信噪比。
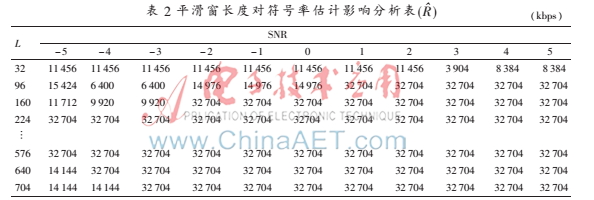
式(12)中互相关能够滤除噪声,当平滑窗长度过小,短时噪声也具有一定相关性时,无法通过互相关滤除,因此平滑窗长度对符号率估计结果准确度有较大影响。表2所示为R=32.704 Mb/s时平滑窗长度对符号率估计影响仿真结果。
由表2知在-5 dB时,平滑窗长低于224时估计性能差,平滑窗长在[224,576]时估计准确,为最佳取值区间,随长度增加估计性能逐渐降低,且随信噪比增大,最佳取值范围变大。根据实验情况,一般取窗长L=(1×M)/(2fs)。
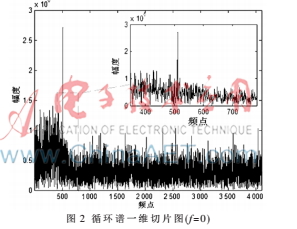
信号x(k)的循环谱Sx?琢(k)为关于(f,A)的三维曲面,当符号率R=32.704 Mb/s、采样率fs=512 MHz、M=8 192的f=0一维切片如图2所示,最大幅度点Amax对应循环频率值即为k=1时循环频率,符号率估计值 =
=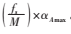 。
。
搜索使得幅度A最大的![9L($AZ2OEELHWNL1F`E[M]X.png 9L($AZ2OEELHWNL1F`E[M]X.png](http://files.chinaaet.com/images/2017/01/25/6362095993273800003922210.png) 需要步进为1在全频域内遍历计算,如图2所示需循环计算M/2=4 096次。利用符号率粗估计结果,缩小循环频率搜索范围至
需要步进为1在全频域内遍历计算,如图2所示需循环计算M/2=4 096次。利用符号率粗估计结果,缩小循环频率搜索范围至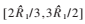 ,可以大大降低计算量,计算次数为:
,可以大大降低计算量,计算次数为:
2.3 符号率估计算法
符号率估计算法主要包括基于功率谱的粗估计和基于改进循环谱的精估计两部分,详细描述如下:
(1)对信号x(k)进行M点FFT变换,得到FFT系数Xk;

3 仿真及分析
3.1 估计准确率分析
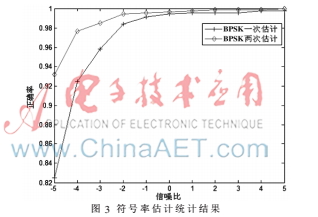
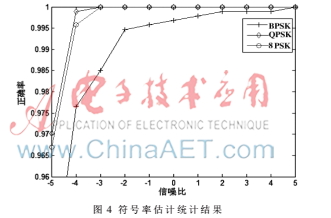
R∈[8 Mb/s,128 Mb/s]以128 Mb/s步进条件下BPSK信号符号率盲估计结果如图3所示,改进符号率估计算法相对于循环谱估计算法信噪比提高超过1 dB。图4所示为改进算法对BPSK、QPSK、8PSK符号率盲估计结果,SNR=-3 dB时QPSK、8PSK符号率估计精确度已达100%,BPSK符号率估计精确度接近98.5%;而SNR=-5 dB时QPSK、8PSK精确度超过96.5%,BPSK精确度超过93%,且可估计符号率范围宽,满足实际应用需求。
3.2 计算量分析
FFT中乘法和加法次数分别为(M/2)log2M和Mlog2M,
FFT系数前后两部分都包含符号率信息,只取前半部分进行运算,平方和累加![@A~Q5S1(U0X]`UXE3~6}8MD.png @A~Q5S1(U0X]`UXE3~6}8MD.png](http://files.chinaaet.com/images/2017/01/25/6362096000166300003803565.png) 等价为:
等价为:
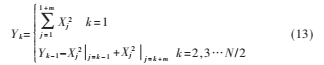
式中Xj2表示FFT第j个系数平方,平方和累加中乘法和加法运算次数分别为:M/2,M+m-2。逼近搜索算法中起始频率f0=M/4,进行8次搜索,第i次搜索所需加法次数为2(1/2i-1+1/2i)f0。完成一次粗估计共需要(M/2) log2M+M/2次乘法和M log2 M+1 533M/512+2m-35次加法。而利用改进循环谱算法完成一次符号率精估计需要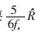 1×M×L次乘法和M×L(5R1/6-1)/fs加法运算。当PSK符号率为32.704 Mb/s时,需要大约122 584次乘法和192 154次加法,计算量仅为参考文献[7]中16 830 464次乘法的7.3‰。
1×M×L次乘法和M×L(5R1/6-1)/fs加法运算。当PSK符号率为32.704 Mb/s时,需要大约122 584次乘法和192 154次加法,计算量仅为参考文献[7]中16 830 464次乘法的7.3‰。
本文主要针对PSK基带符号率盲估计展开研究,利用循环搜索逼近技术实现了功率谱累加序列拐点频率提取,完成符号率粗估计,分析了功率谱累加长度对粗估计精度的影响。利用互相关理论,对循环谱算法进行改进,提高了抗噪性;在分析平滑窗长度及循环频率搜索范围对循环谱符号率估计精度、算法复杂度影响的基础上,结合粗估计实现了最优平滑窗长和循环频率搜索范围的选取,改善了计算量。
参考文献
[1] Wang Long, Zhang Gengxin, Bian Dongming, et al. Blindsymbol rate eestimation of satellite communication signal byhaar wavelet transform[J]. Journal of Electronics, 2011,28(2):198-203.
[2] 金艳, 姬红兵. 基于循环自相关的PSK信号盲参数估计新方法[J]. 西安电子科技大学学报, 2006,33(6):892-895.
[3] MOSQUERA C, SCALISE S,Lopez-Valcarce R. Non-data-aided symbol rate estimation of linearly modulated signals[J].IEEE Transactions on Signal Processing,2008,56(2),664-674.
[4] 黄春琳, 柳征, 姜文利,等.基于循环谱包络的扩谱直序信号的码片、时宽、载频、幅度估计[J]. 电子学报,2002,30(9):1353-1356.
[5] 金艳, 姬红兵. 基于循环自相关的PSK信号码速率估计的噪声影响分析[J]. 电子与信息学报,2008,30(2):505-508.
[6] 郑天堃, 姚远程, 秦明伟. 基于循环谱的数字信号的自动识别[J]. 电子技术应用,2013,39(9):102-104.
[7] 崔伟亮, 江 桦, 李剑强,等.改进的循环谱估计快速算法与性能分析[J]. 电子与信息学报,2011,33(7):1594-1599

