黄 静，邵 兵，王剑飞
（国网重庆市电力公司万州供电分公司，重庆404000）
摘 要： 无线供电系统中线圈、线圈间互感、补偿电容、谐振频率各个参数之间相互制约、相互影响，系统的设计是一个多参数、多变量的优化问题。以往的参数优化一般是单参数优化而且只优化到互感，并没有优化到具体的匝数，系统设计需要较大修正。为解决此问题，在得到系统的传输功率和效率模型的基础上，利用线圈匝数与自感互感的关系，以PS型拓扑为优化对象，给出了系统的非线性数学规划模型，利用遗传算法得出了系统的最优设计参数。最后，通过实验研究证明了理论分析与设计方法的正确性。
关键词： 无线供电；参数优化；数学规划；遗传优化
中图分类号： TM74文献标识码： A文章编号： 0258-7998(2014)12-0076-03
0 引言
感应耦合电能传输(Inductively Coupled Power Transfer，ICPT)，实现了用电设备与供电线路之间非物理接触下的能量传输，特别适合在一些潮湿、易燃易爆条件下取代传统供电方式[1-3]。对于ICPT系统，耦合机构包括2组线圈，2个补偿电容，为了使传输功率达到最大，需要对线圈匝数，补偿电容，系统运行频率等进行合理规划，这是一个多变量、多约束的非线性优化问题。传统的参数设计方法是采用逐步测量设计的方式[4-5]，操作复杂且不易得到最优结果。如果采用求导方式则需要数学模型函数可导且一次只能针对一个参数求出最优，不能保证系统多个参数最优，这样设计的参数在实际应用中需要较大的修正，没有减小ICPT系统设计难度[6]。遗传算法对多参数优化问题具有很快的收敛速度和良好的全局寻优能力[7]，本文拟采用遗传算法对ICPT系统参数进行优化设计。
1 PS型ICPT系统功率和效率模型
对于PS型ICPT系统，其结构框图如图1所示。其中Vi是发射线圈谐振回路的等效电压源，Cp、Co分别是发射端和接收端电感Lp、Ls的补偿电容，Rp、Rs分别是发射端和接收端的等效串联电阻，Ro为负载，Zps为接收线圈到发射线圈的反射阻抗，Mps为两线圈之间的互感系数。
根据互感原理，对于PS拓扑结构，在发射线圈和接收线圈均处于谐振状态，谐振角频率为ω0，且发射端线圈电流为IP的情况下，负载Ro上电压以及电流有效值分别为：
由式(1)可得到PS系统的传输功率为：
![}CF%A4BQGU@UB[VXJ4UAL]M.png](http://files.chinaaet.com/images/2017/01/25/6362096520846800009357656.png "}CF%A4BQGU@UB[VXJ4UAL]M.png")
系统的工作效率可表示为：
其中，Po为系统输出功率，Pi1为原边的线圈损耗，Pi2为副边的线圈损耗，可求得Pi1、Pi2分别为：
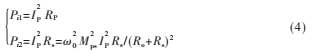
由式(2)～(4)得到系统的效率模型为：
![Y$%$)7W(5)I2I9]{$~0{XO2.png](http://files.chinaaet.com/images/2017/01/25/6362096523317900007998656.png "Y$%$)7W(5)I2I9]{$~0{XO2.png")
由于实际系统中负载远大于负载端线圈内阻[8]，所以系统传输效率可简化为：
2 互感与线圈匝数及线圈内阻模型
首先建立系统的自感以及互感关于线圈匝数、半径，线圈间距的表达式。
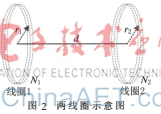
对于如图2所示的两组螺旋线圈，根据参考文献[9]，线圈1的自感L1、线圈2的自感L2分别为：
![KQX}M]U4JL671PTR6ZG9_JJ.png](http://files.chinaaet.com/images/2017/01/25/6362096524508700007116001.png "KQX}M]U4JL671PTR6ZG9_JJ.png")
线圈1和2之间的互感M为：
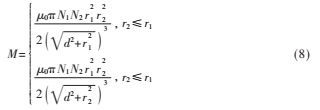
其趋肤深度为：
其中，![YA1XC]8W[@CYM{$S4%F33JR.jpg](http://files.chinaaet.com/images/2017/01/25/6362096531903000004003361.jpg "YA1XC]8W[@CYM{$S4%F33JR.jpg")
为导线中电流的角频率，![EFFFS[T]{O2GIEE(WN$7(LV.jpg](http://files.chinaaet.com/images/2017/01/25/6362096532336600006201724.jpg "EFFFS[T]{O2GIEE(WN$7(LV.jpg")
为导线材料的电导率，对于铜导线，其电导率为5.8×107 S/m。那么单位长度的电阻为:
![52SJR}Z5`T$]$O{Q}QDUERL.png](http://files.chinaaet.com/images/2017/01/25/6362096526231800005023791.png "52SJR}Z5`T$]$O{Q}QDUERL.png")
其中，
为导线的半径。对于螺旋线圈，当线圈匝数为N，线圈半径为r时，忽略两根绕线间的间距，此时线圈的内阻![}0BI0OKT9ZS0D)FL]I6S(%V.jpg](http://files.chinaaet.com/images/2017/01/25/6362096533613900009332294.jpg "}0BI0OKT9ZS0D)FL]I6S(%V.jpg")
为：
3 PS型ICPT系统数学规划模型
结合电路中的一些实际情况，令Cp、Cs的额定电压分别为VCp_r、VCs_r则系统应满足：
式中为补偿电容Cp、Cs上的谐振电压。
根据实际情况，线圈匝数、线圈半径都有最大值以及最小值。
式中，Np-m、Np-n、Ns-m、Ns-n分别为发射线圈及接收线圈匝数的最大值与最小值。rp-m、rp-n、rs-m、rs-n分别为相应线圈半径的最大值与最小值。
根据实际情况，线圈之间也有最大值以及最小值，传输效率应有一个最小值。
式中，dps-m、dps-n分别为发射线圈与接收线圈之间距离的最大值与最小值，当线圈为f，电感为L时，线圈的补偿电容为：
对于PS型拓扑，当发射线圈电流Ip保持恒定时，系统的输出功率为：
若已知Ip和Ro及上述所提到的各器件参数最大、最小及额定值，优化f、Np、Ns、rp、rs、dps，在满足系统传输效率的条件下使系统的传输功率最大，至此得到系统的非线性规划数学模型：
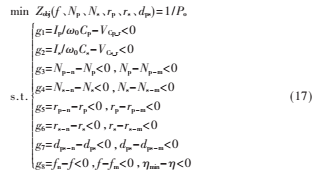
从式(17)可以看出，线圈的参数设计是一个多变量、多约束的非线性优化问题，引入遗传算法对其进行求解与分析，优化结果可利用MATLAB的遗传算法工具箱获得。
以PS型拓扑的非线性规划模型为优化对象，系统的已知条件为：Ip=10 A，Ro=50 Ω；参数约束值分别为：Vcp_r=Vco_r=600 V，Vcs_r=Vcr_r=1 200 V，Icp_r=Ico_r=30 A，Ics_r=Icr_r=60 A，优化变量f、Np、Ns、rp、rs、dps的解空间分别为[10 000 100 000]、[1 200 ]、[1 200]、[0.1 0.5]、[0.1 0.5]、[0.01 0.5]，同时设定最小传输效率为65%，利用遗传算法在约束条件下对式（17）进行参数优化得到系统的最优参数为：f=20.001 kHz，Np=45，Ns=52，rp=0.18 m，rs=0.14 m，dps=0.074 m，![}B]LTF)RLR(A7KGN)UX_EW3.png](http://files.chinaaet.com/images/2017/01/25/6362096547831900009259660.png "}B]LTF)RLR(A7KGN)UX_EW3.png")
=0.72，优化得到的参数均满足约束。
4 实验研究
为进一步验证参数优化的正确性，利用优化参数搭建了一个PS型拓扑ICPT系统实验样机，其主电路拓扑如图3所示。
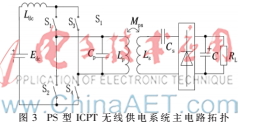
人为使线圈匝数偏离优化参数，其他参数均与优化参数保持一致，图4、图5即为优化前与优化后系统发生线圈谐振电流，输入电压，电流波形图，由图可以看出在线圈发射电流基本保持不变的前提下，优化后的系统能够传输更大的无线电能，输入电压基本不变但系统电流从467 mA增加到974 mA。
在实际的系统中，传输功率和传输效率一般无法达到同时为最大值，此时应依据实际情况来选择，如果系统传输功率为主要因素，那么应使效率满足要求的情况下以最大传输功率为目标，若效率为重点考虑的因素，那么应在系统满足功率要求的情况下，以效率最高为优化目标进行优化设计。
5 结论
本文首先基于互感模型对PS型ICPT系统的传输功率、传输效率进行了建模研究，以PS型拓扑为优化对象，建立了该拓扑结构的非线性规划数学模型，以该模型为对象利用遗传算法对系统参数进行了优化设计，最后设计了实验样机来验证优化结果，验证了系统参数在设计要求内且具有较高的传输功率和传输效率，此优化方法可直接得出系统具体的线圈匝数便于工程设计，具有较好的实际应用价值。
参考文献
[1] WU H H，BOYS J T，COVIC G A.An AC processingpickup for IPT systems[J].IEEE Transactions on PowerElectronics，2010，25(5)：1275-1284.
[2] 王路，陈敏，徐德鸿，等．磁悬浮列车非接触紧急供电系统的工程化设计[J].中国电机工程学报，2007，27(18)：67-70．
[3] BINGNAN W，KOON H T，NISHINO T，et al.Experimentson wireless power transfer with metamaterials[J].AppliedPhysics Letters，2011，98(25)：1-3.
[4] VILLA J L，SALLAN J，LLOMBART A，et al．Design of ahigh frequency Inductively Coupled Power Transfer systemfor electric vehicle battery charge[J]．Applied Energy，2009，86(3)：355-363．
[5] SALLAN J，VILLA J L，LLOMBART A，et al．Optimaldesign of ICPT systems applied to electric vehicle batterycharge[J]．IEEE Transactions on Industrial Electronics，2009，56(6)：2140-2149
[6] 夏晨阳，孙跃，贾娜，等.耦合磁共振电能传输系统磁路机构参数优化[J].电工技术学报，2012.27(11)：139-145.
[7] DEB K．An efficient constraint handling method for geneticalgorithms[J]．Computer Methods in Applied Mechanics andEngineering，2000，186(2-4)：311-338．
[8] WANG C S，COVIC G A，STIELAU O H.Power transfercapability and bifurcation phenomena of loosely coupledinductive power transfer systems[J].IEEE Transactions onIndustrial Electronics，2004，51(1)：148-157.
[9] AZAD U，JING H C，WANG Y E.Link budget and capacityperformance of inductively coupled resonant loops[J].Antennasand Propagation，IEEE Transactions on，2012，60(5)：2453-2461.