张昊，叶宇煌

　　（福州大学 物理与信息工程学院，福建 福州 350116）

       摘要：测斜仪在石油勘探、地质勘查等方面已成为一种有力的工具，但基于磁通门的测斜仪存在着易受磁场干扰的缺点，导致其测量精度降低，甚至无法工作。为了解决这一问题，提出了一种基于捷联惯性导航原理的连续测斜算法。算法利用微惯性传感器MPU6050获取姿态数据，采用四元数方法进行姿态解算，最终得到钻探过程中的倾斜角、方位角以及工具面角等数据。通过仿真验证，得到测量误差曲线。仿真结果表明，该算法可以实现全方位井眼轨迹连续测量，提高了测量效率。

　　关键词：测斜仪；捷联惯性导航；四元数；姿态解算

　　中图分类号：TP391.9文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.01.005

　　引用格式：张昊，叶宇煌. 基于微惯性传感器的测斜仪姿态算法的研究［J］.微型机与应用，2017,36（1）：15-17.

0引言

　　随着科学技术的发展，煤炭开采范围也越来越大，复杂的地质环境使得安全生产问题日益严重。查明工作面的地质构造以及精确的工程钻探，都需要精度高、稳定性好且能全方位测量钻孔轨迹的测斜仪。目前存在的测斜仪主要有两类：一类是基于磁通门的测斜仪，但这种测斜仪在铁矿丰富的地区会受到极大的干扰，以至于无法工作；第二类采用机械式陀螺作为测量单元，虽然不受周围环境的影响，但它只能进行静态单点测量，测量时间长［13］。

　　本文将捷联惯性导航应用在测斜仪中，利用测斜仪中的三轴陀螺仪和三轴加速度微惯性传感器测得姿态数据，输出的数据经过姿态解算，可直接输出测斜仪的三个姿态角信息。捷联惯性导航直接将惯性器件捆绑在载体之上，不依赖于外界信息，因此具有结构简单、体积小、成本低、可靠性高等优点［4］。

1捷联惯性导航原理

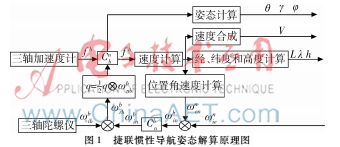
　　由于惯性传感器是与载体捆绑在一起的，因此与载体一起运动，陀螺仪测得的角速度和加速度计测得的比力都是在载体坐标系当中的，因此只有将其中的角速度和比力信息转换到导航坐标系中，才能够实现对载体姿态的解算［5］，基本原理如图1所示。所以姿态解算算法是捷联惯性导航的关键技术，解算算法的好坏直接影响导航系统的精度。常见的姿态解算方法有以下4种［6］：

　　（1）欧拉角法，当俯仰角为90°时，欧拉微分方程存在着退化问题，不能全姿态工作，只适合应用在水平姿态变化不大的载体上。

　　（2）方向余弦法可以全姿态工作，但是需要解算9个微分方程，计算复杂。

　　（3）四元数算法只需要求解4个微分方程，计算简便，但引入不可交换性误差，一般不适合于激烈运动的运动载体的姿态解算。

　　（4）等效旋转矢量法，通过多子样算法弥补了四元数算法存在的不可交换性误差的缺点，适用于高动态运动载体的姿态解算。子样数越多，姿态解算的精度也就越高，同时计算复杂度也随之增加。相比于四元数法的计算量增加了30%。

　　四元数法和等效旋转矢量法都能够全姿态工作且精度高，所以在工程中经常用到。虽然四元数法相对于等效旋转矢量法存在不可交换性误差，不能在激烈运动的载体上应用，但可以应用到低速运动的测斜仪中。

　　1.1坐标系定义

　　惯性坐标系记为i，原点位于地心，xi指向春分点，zi沿地球自转轴，yi与xi、zi轴构成右手系。选取地理坐标系作为导航坐标系，记为n系，原点位于载体质心，zn分别指向所在地的东、北、天。载体坐标系记为b系，xb、yb、zb分别指向右、前、上。

　　1.2坐标变换

　　两坐标系间任何复杂的角位置关系都可以看作有限次基本旋转的复合，变换矩阵等于基本旋转确定的变换矩阵的连乘，连乘顺序依基本旋转的先后次序由右向左排列。所以载体坐标系与导航坐标系之间的转换可以用下面的矩阵表示：

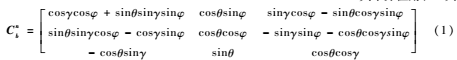　　其中φ为方位角（航向角），θ为井斜角（俯仰角），γ为工具面角（横滚角），Cnb称为载体的姿态矩阵。式中Cnb与旋转次序有关，即当旋转角φ、θ、γ不都为小角时，对应于不同的旋转次序，坐标系n的最终空间位置是不同的，这就是常说的有限转动的不可交换性。但当φ、θ、γ都为小角时，忽略小角间的高阶小量,式（1）变为：

　　式中，φ、θ、γ的单位为弧度。此时由φ、θ、γ构成的列向量［φθγ］T可视为三维空间矢量，各分量正负号的规定为：当产生小角的旋转方向与坐标轴指向相同时该小角取正，否则取负。此时旋转后坐标系的最终角位置与旋转次序无关，这就是常说的无限转动与次序无关［7］。由于直角坐标系之间的变换矩阵为单位正交矩阵，所以如果在坐标系b至坐标系n的等效旋转中各坐标系都保持为直角坐标系，则根据正交单位矩阵的性质有［8］：

　　Cnb=(Cbn)－1=(Cbn)T（3）

　　2四元数算法

　　四元数是由4个元构成的数：

　　q=q1+q2i+q3j+q4k（4）

　　式中，q1、q2、q3、q4是实数，i、j、k是相互正交的单位向量，又是虚单位－1。根据欧拉定理，空间中两坐标系的相对位置，可以等效为动坐标系绕某一瞬轴u（单位向量）转过角θ一次完成。u和θ可以用来表示一个四元数：

　　2.1四元数表示的姿态矩阵

　　式（5）描述了刚体的定点转动，即当只关心b系相对于n系的角位置时，可认为b系是由n系经过无中间过程的一次性等效旋转形成的，q包含了这种等效旋转的全部信息：u为旋转瞬轴和旋转方向，θ为转过的角度。因此可以确定出b系至n系的坐标变换矩阵为：

　　由式（1）与式（6）可以得出:

　　θ主=arcsin(T32)

　　γ主=arctan(－T31/T33)

　　φ主=arctan(T12/T22)（7）

　　其中方位角和工具面角的真值可以按照表1和表2进行确定。

　　2.2四元数的微分方程及求解

　　四元数的姿态更新微分方程表示如下：表1方位角的真值T11T21φ0+90°0-－90°++φ主-φ主-+φ主+180°--φ主－180°表2工具面角的真值T33γ主γ++-γ主-+γ主－180°--γ主+180°dqdt=12qωbnb（8）

　　式中ωbnb=ωxωyωzT。写成矩阵形式：

　　其中，ωbnb可由下式计算得到：

　　ωbnb=ωbib－Cbn(ωnie+ωnen)（11）

　　式中，ωbib为三轴陀螺仪的输出，表示载体坐标系相对于惯性坐标系的角速度； ωnie表示地球坐标系相对于惯性坐标系e在载体坐标系中的角速度；ωnen表示导航坐标系相对于惯性坐标系在导航坐标系下的角速度。

　　利用毕卡求解法对式（10）进行解算得：

　　3验证

　　利用MATLAB软件对以上算法进行仿真验证。设计的方位角、井斜角和工具面角的变化规律如图2所示，初始方位角为68.9°，初始井斜角为0°，初始工具面角为178°；采样频率为100 Hz。由于加入仪器误差后使得误差来源不明，所以本次仿真实验默认惯性传感器的输出为理想状态下的输出。通过本文设计的算法对传感器的输出进行解算，最终结果如图3所示。　　

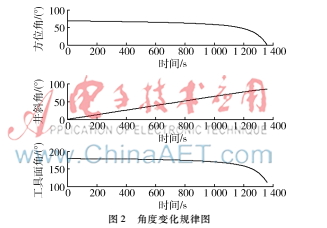
　　由图3可以看出方位角的理论解算误差控制在±1°以内，井斜角误差控制在±0.1°以内，工具面角误差控制在±1°以内，具有良好的解算精度，证明本文提出的解算方法有效。

4结论

　　本文提出了一种新的基于捷联惯性导航原理的连续测斜算法，并进行了模拟仿真。仿真结果表明该解算算法可以实现解算姿态的功能，在保证测量精度的同时，比之前的静态测量缩短了测量时间，提高了测量的效率。但该算法在长时间测量的情况下可能会出现测量精度降低的情况，这可能是因为积分的累计误差造成，有待进一步的研究。

参考文献

　　［1］ 谢子殿, 朱秀. 基于磁通门与重力加速度传感器的钻井测斜仪［J］. 传感器与微系统, 2004, 23(7):30-33.

　　［2］ NOY K A, LEONARD J G. A new rate gyroscopicwellbore survey system achieves the accuracy and operational flexibility needed for today's complex drilling challenges［C］.SPE/IADC Drilling Conference, Society of Petroleum Engineers, 1997.

　　［3］ 刘宇, 李秋俊, 刘俊. 基于压电陀螺的快速方位测井短接［J］. 电子测量与仪器学报, 2007, 21(2):90-94.

　　［4］ 张春慧. 高精度捷联式惯性导航系统算法研究［D］. 哈尔滨：哈尔滨工程大学, 2005.

　　［5］ 丁君. 基于微惯性传感器的姿态算法研究［D］. 上海：上海交通大学, 2013.

　　［6］ 张露. 基于捷联惯导的采煤机位姿解算算法研究［D］. 西安:西安科技大学, 2014.

　　［7］ 秦永元. 惯性导航［M］. 北京：科学出版社, 2014.

　　［8］ 彭劲松. 机载激光捷联惯导优化算法研究［D］. 西安：西北工业大学, 2006.