张俊俊，何良华

　　（同济大学 电子与信息工程学院，上海 201800）

        摘要：深度学习是一类新兴的多层神经网络学习算法，因其缓解了传统训练算法的局部最小性，故引起机器学习领域的广泛关注。但是，如何使一个网络模型在选取任意数值的隐藏层节点数时都能够得到一个比较合适的网络结构是目前深度学习界普遍存在的一个开放性问题。文章提出了一种能够动态地学习模型结构的算法——最大判别能力转换法，根据Fisher准则来评估隐藏层每一个节点的判别性能，然后通过动态地选择部分隐层节点来构建最优的模型结构。

　　关键词：深度学习；最大判别能力转换法；Fisher准则；深度信念网络

　　中图分类号：TP183文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.01.018

　　引用格式：张俊俊，何良华. 动态深度信念网络模型构建［J］.微型机与应用，2017,36（1）：59-61，65.

0引言

　　深度学习可以让那些拥有多个处理层的计算模型来学习具有多层次抽象的数据的表示。这些方法在许多方面都带来了显著的改善，包括最先进的语音识别、视觉对象识别、对象检测和许多其他领域，例如药物发现和基因组学等。

　　然而，在很多应用问题中，经常会遇到很高维度的数据，高维度的数据会造成很多问题，例如导致算法运行性能以及准确性的降低。特征选取（Feature Selection）技术的目标是找到原始数据维度中的一个有用的子集，再运用一些有效的算法，实现数据的聚类、分类以及检索等任务。好的特征可以提供数据的语义和结构信息，使简单的模型结构也能取得良好的学习效果。然而，如何选取恰当的特征并获取一个准确的模型结构仍然是深度学习模型构建的一个开放性问题。近年来很多相关工作［12］被提出，使得特征选取越来越多地受到关注，另外一些关于数据谱分析以及L1正则化模型的研究，也启发了特征选取问题一些新的工作的开展。并且，随着计算机与网络的发展，人们越来越多地关注大规模数据的处理问题，使得研究与应用能够真正衔接在一起。传统的特征选取方法普遍采用依赖于经验或者模型参数的调整，例如dropout［3］、dropconnect［4］等。这些方法都要求在模型使用的初始时结构就必须确定下来，并在模型的整个训练过程中结构都不再发生变化。这在一定程度上限制了模型的表达能力。

　　基于此，本文提出一种能够动态地学习模型结构的算法——最大判别能力转换法，来根据Fisher准则评估隐藏层每一个节点的判别性能，然后通过动态地选择部分隐层节点来构建最优的模型结构。其中，对于隐藏层节点数目的选取是通过考虑模型计算复杂度以及信息保留程度权衡后的计算结果。

1深度信念网络

　　深度学习是具有多层隐藏层的神经网络结构，这种网络具有更好的学习特征的能力，对原始特征具有更本质的描述，从而更利于可视化或分类。其中，深度信念网络［5］（Deep Belief Network, DBN）是比较具有代表性的模型之一，也是最简单的深度学习模型。为了有效克服深度神经网络在训练上的难度，其采用了无监督贪婪学习的逐层初始化方式（即BP算法）。

　　深度信念网络是一种生成型概率模型，是由多个限制玻尔兹曼机（Restricted Boltzmann Machine，RBM）堆叠组成的层次结构。

　　DBN是通过堆叠RBMs而成，如图1所示，使用输入样本观测值作为第一层RBM的输入，将由输入训练出的输出作为第二层RBM的输入，以此类推，通过叠加RBM模型完成深度模型的构建。

　　RBM训练模式受物理学的能量模型启发，事物在能量最低时所处的状态是最稳定的，于是构建RBM的稳态就成了状态优化的问题，这一问题可以进一步转化为求极值与优化的问题。对于图1所示的RBM模型，假设输入层节点为v，隐藏层输出节点为h，输入输出层之间的权重为w，那么输入层向量v与输出层向量h之间的能量函数E为：

　　其中，a、b分别为对应可视层和隐藏层的偏移，V、H分别表示可视层和隐藏层的节点数。那么，由能量函数得到可视层v与隐藏层h之间联合函数为：

　　其中尖括号的运算表示相对于下标的预期分布内积，由此，log似然函数梯度权重的更新规则如下：

　　Δwij=ε(<vihj>data-<vihj>model)(8)

　　其中ε表示学习率。然而上式中计算后一项需要花费很多额外的时间，为了减小这种额外花费，对比散度（Contrastive Divergence）方法被用来计算梯度，所以新的更新规则如下：

　　Δwij=ε(<vihj>data-<vihj>recon)(9)

　　后一项表明了重构后的可视层与隐藏层的期望值，实践证明该方法得到充分应用后具有良好的特性。相比于传统的Sigmod信度网络，通过以上方式学习的RBM具有权值容易学习的优点。

　　深度学习是具有多层隐藏层的神经网络结构，这种网络具有更好的学习特征的能力，对原始特征具有更本质的描述，从而更利于可视化或分类。为了有效克服深度神经网络在训练上的难度，采用了无监督贪婪学习的逐层初始化方式。深度信念网是其中比较具有代表性的模型之一，也是最简单的深度学习模型。

2结构计算

　　每一个隐藏层节点代表了映射空间中的一个维度，将可视层映射到隐藏层的过程就类似于一种空间变换，也就是把源数据转换到了一个更加容易区分的新的映射空间。然而，这种空间变换的方式，例如：PCA、ICA、LDA等，所产生的各个维度在不同的空间中有不同的判别能力。

　　故本文基于Fisher准则［6］，评估每个节点的判别能力，然后根据最大判别能力转换法选取部分隐藏层节点来构成新的映射空间，剔除冗余或者对判别能力产生副作用的投影维度，来提高此投影空间判别性能。

　　2.1节点评估

　　Fisher准则函数通过计算每个节点的类间与类内的比值来确定其在此投影空间中每个维度的判别能力。

　　定义数据集中共有N个样本属于C类，每一类分别包含Nc个样本，uc、u分别表示样本Xc在第c类的均值以及所有样本的均值。第j个特征的Fisher的值表示为：

　　2.2最具判别能力转换法

　　Fisher准则仅仅能够判别每个特征的判别性能，却无法计算每层隐藏层具体多少个节点能够获取最大的描述能力以及判别能力。本文基于能够最大程度缩减原始高维输入样本与重构后的输入样本之间的误差来提取部分特征，以此来提高模型的整体判别性能。

　　误差计算方式如下：

　　其中，xi是原始的输入样本，hjWji是重构后的输入样本。

　　W*=argminWR(14)

3实验结果

　　实验从两方面来验证最具判别能力转换法（MDT）的有效性以及可行性。第一个实验基于Iris数据库，通过对比Laplacian Score［7］方法与Data variance方法来验证Fisher Score方法的优越性能；第二个实验是基于Mnist数据库来评估MDT算法。

　　3.1Iris数据库

　　Iris数据库也称鸢尾花卉数据集，是一类多重变量分析的数据集。数据库包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性（F1：sepal length；F2：sepal width；F3：petal length；F4：petal width）。大量研究证明对分类起显著作用的属性为F3与F4。

　　Data variance方法被认为是最简单的无监督分类算法，它可以作为一种对特征选择与提取的标准之一，另一种标准是Laplacian Score，它是根据Laplacian Eigenmaps与Locality reserving Projection来评判的。实验结果如图2所示。

　　图2显示，根据Data variance标准，特征排序为：F3，F4，F1，F2；根据Laplacian Score排序结果为：F4，F3，F1，F2；而根据Fisher Score排序结果为：F3，F4，F1，F2。由此可知，Fisher Score能够实现比较好的特征评估。

　　3.2Mnist数据库

　　Mnist数据库包含有60 000个训练样本和10 000个测试样本，每个样本大小为28×28，共分为10类。

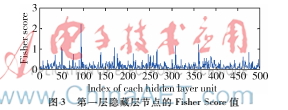
　　本实验通过对比深度信念网络（DBN）不同隐层节点数目发现，当第一隐层节点为500、第二隐层节点为2 000时，模型训练效果最好，误差最低，结果如表1表示。基于该最优结构，我们希望MDT算法能够进一步降低模型分类误差。首先计算出第一层隐藏层中每一个节点的Fisher Score值，如图3所示。

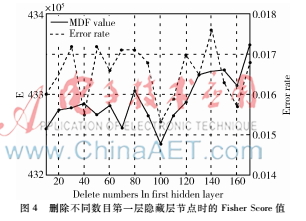
　　然后，图4展示了依次删除第一层隐藏层不同节点数目后模型的错误率以及MDF值。最后，发现删除100个节点时，MDF值最小并且模型的错误率也达到最小。　　

4结论

　　本文提出了一种新颖的构建DBN模型结构的算法，其基于Fisher准则以及最大判别能力转换法来动态地删除隐层节点以达到优化结构的目的，不同于现有的各种针对DBN模型所做的规则化算法。基于多个数据库的实验结果也证实了本算法确定能够获得比较好的隐层节点数目。

参考文献

　　［1］ HINTON G E,SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks［J］. Science, 2006, 313(5786):504-507.

　　［2］ SALAKHUTDINV R, HINTON G. Semantic hashing［J］. International Journal of Approximate Reasoning, 2009, 50(7):969-978.

　　［3］ HINTON G E, SRIVASTAVA N,KRIZHEVSKY A, et al. Improving neural networks by preventing coadaptation of feature detectors［J］. Computer Science, 2012, 3(4):212-223.

　　［4］ SRIVASTAVA N. Improving neural networks with dropout［J］. Journal of Chemical Information and Modeling, 2015, 53(9):1689-1699.

　　［5］ HINTON G E,OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets［J］. Neural Computation, 1960, 18(7):1527-1554.