朱桂林，张栋良，陈辉

　　（上海电力学院 自动化工程学院，上海市电站自动化技术重点实验室， 上海 200090）

       摘要：针对同一物体不同视角下获得的三维点云数据，提出一种基于改进特征点对选取的三维点云配准方法。在欧氏距离的基础上选取与目标点最近的三点均值为对应点，并应用邻域比值法来剔除错误点，结合Kd tree提高搜索速度，实现最终点云配准。实验结果表明，该方法具有可行性，相比传统ICP算法，其匹配精度和效率明显提升。

　　关键词：点云配准；ICP算法；最近点选取；错误点剔除

　　中图分类号：TP391文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.01.022

　　引用格式：朱桂林，张栋良，陈辉. 基于改进特征点对选取的三维点云配准［J］.微型机与应用，2017,36（1）：73-75.

0引言

　　利用激光扫描仪对建筑物进行扫描，得到其点云信息，从而建立物体的三维模型，成为当下研究的热点［1］。但在实际操作中往往受到各种限制，无法一次性精准地获得待测物体的全部点云信息。为了在后期重建过程中得到较为完整的三维模型，实际测量中需要对待测物体进行多角度、多次数的测量并且通过点云配准将获得的点云数据变换到同一坐标中［2］。

　　针对点云配准过程，迭代最近点算法（Iterative Closest Point，ICP）［3］是目前比较经典的配准方法。其优点是对初始点云形状要求低，配准过程简单，结果相对收敛。但是该算法也存在着一些不足，如：要求待配准两片点云的数据为包含关系，两片点云中的数据点满足一一对应关系；其次随着点云数量的增加计算代价也相应增加；最后在对应点寻找过程中，仅仅假设两片点云中欧氏距离最近的点为所求的对应点，由于这种假设过于理想化，在实际操作过程中可能会出现错误的对应点，使配准陷入局部最小值导致配准失败。针对传统ICP算法的不足，国内外学者在配准策略、配准元素、错误点剔除以及误差度量等方面对算法进行了改进与优化，使传统ICP算法在性能方面得到提高［47］。

　　本文在三维点云配准过程中分以下两步：

　　（1）提出了一种改进的特征点对选取方法，过程采用Kd tree查找最近点以提高搜索效率。对于原始点云中的一点，寻找其在目标点云中欧氏距离最近的三点并计算三点的平均值，以此作为对应点，然后利用邻域比值的方法来剔除误匹配点，提高匹配精度，最后结合四元法［89］求取旋转矩阵R及平移向量T。

　　（2）根据计算得到的初始矩阵R及平移向量T，利用ICP算法对两片点云进行配准。

1算法过程

　　1.1对应点对选取和剔除错误点对

　　（1）对应点对求取

　　利用Kd tree计算点集P中任一点pi(i=1,2，...)在目标点集Q中与其欧氏距离最近的三个点q1、q2、q3，分别计算三点x、y、z的均值构成新的坐标(=())，pi与构成对应点对(pi)。

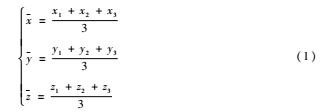
　　（2）错误点对剔除

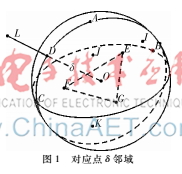
　　点集采集过程中不可避免地引入噪声点，因此在对应点的计算过程中可能会产生错误对应点对，本文采用邻域点集比值法来检验对应点对是否符合标准，并剔除错误点对。由对应关系可知，如果两个点是对应点则其在各自δ邻域内所包含的点数应该近似相等。实验过程中在点云P和点云Q内分别计算pi与以δ为半径所构成邻域内点的个数m和n。若mn=γ(0.9≤γ≤1.1)，保留对应点对，否则剔除。如下图1。

　　1.2四元数法求配准矩阵R和T

　　对于原始点云数据,在求取旋转矩阵R和平移向量T时，采用四元数法，其计算过程如下：

　　（1） 分别计算点集{pi}和点集{qi}的质心：

　　（5）求K的特征值并且求解最大特征值所对应的单位特征向量d,d=［d1d2d3d4］T

　　（6）求解旋转矩阵R

　　（7）根据R与T的对应关系求取平移向量T

　　T=μq－Rμp（7）

　　1.3改进ICP算法的配准过程

　　ICP算法在本质上是使用最小二乘的方法对待配准的点云数据进行最优匹配。计算过程中重复进行选择对应关系点对，计算最优旋转矩阵R和平移矢量T,直到满足正确的收敛精度函数E并使E达到最小值。

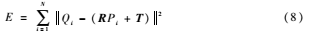
　　式中,Pi为原数据的初始点集；Qi为Pi对应目标数据点集的最近点；R为3×3旋转矩阵；T为3×1平移矢量。

　　配准过程具体如下：

　　（1） 读取初始点云并在初始点云中选取点集pi；

　　（2） 利用Kd tree对点集p中任一点pi计算其在点集q内欧氏距离最近的三个点q1、q2、q3，并计算，过程对应点对(pi)；

　　（3）采用邻域点集比值法剔除不符合条件的对应点；

　　（4）采用四元数法计算旋转矩阵R和平移矢量T；

　　（5）迭代终止判断：若ek－ek+1<ε，则终止迭代，否则重复（2）~（5）直至结果满足收敛条件。其中ε表示大于零的阈值。

2实验论证

　　本实验采用的实验数据来自斯坦福兔子（Stanford Bunny），分别选取不同视角下的两组点云数据作为原始点云和目标点云，两片点云的数量分别为35 947和30 379。实验平台为：CPU 2.70 GHz，内存4 GB，Windows7 32位操作系统；算法在MATLAB 2011b环境中实现，实验选取的ε=0.005。

　　实验过程中为了进一步验证本文方法的可行性，减少中间误差，在与传统ICP算法比较过程中，本文分别从迭代次数和迭代点云数量两方面（即更改迭代次数以及更改点云数量）进行验证。

　　2.1迭代次数

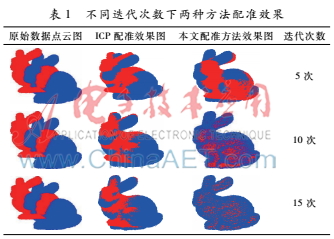
　　为消除实验过程中次数对结果的影响，对于Stanford Bunny操作过程中分别选取迭代次数为5次、10次以及15次作为一组参照进行对比验证，实验结果如表1。表1不同迭代次数下两种方法配准效果原始数据点云图ICP配准效果图本文配准方法效果图迭代次数5次10次15次从表1可得出，在使用相同的初始点云数据情况下：（1）迭代次数相同时，本文所采用的改进ICP算法所得出的配准效果明显优于传统ICP算法；（2）随着迭代次数增加，传统ICP算法配准效果逐级优化，但是采用改进算法所得到的配准图像逐级优化效果更加明显。

　　为了进一步比较改进算法相对于传统ICP算法的优势，在基于不同迭代次数情况下分别从配准时间以及配准误差两个方面进行列表对比，本文采用均方根误差［10］（Root Mean Square，RMS）来表示配准误差，对比情况如表2。

　　从表2可以看出，在同一迭代次数下改进算法与传统ICP算法相比在配准误差以及配准时间上都得到了明显优化，这种优化随着迭代次数的增加变得更加明显，例如迭代次数为5时，传统ICP算法配准时间为240.37 s，配准误差为0.122 4，而改进的ICP算法配准时间为22.70 s，配准误差为0.066 0；当迭代次数为15时，传统ICP算法配准时间为610.45 s，配准误差为0.037 6，此时改进ICP算法配准时间仅为40.89 s，配准误差为0.002 4。综上，无论是在同一迭代次数的横向对比还是在不同迭代次数的纵向对比中，本文采用的配准方法在配准效果、配准时间以及配准误差上都要明显优于传统ICP算法。

　　2.2迭代点云数量

　　为了消除点云数量对两种方法产生的误差，本文在基于Bunny数据基础上，选取初始点云数量分别为400点、3 600点、6 400点以及32 400点，并在迭代次数同为15次的基础上进行对比验证，结果如表3。

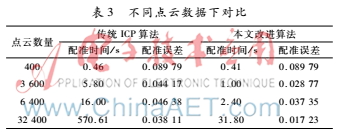
　　根据表3，在初始点云数较少的情况下，改进方法与传统ICP方法相比在配准时间和配准误差上均有进步，但差别并不明显，如在点云数为400点时二者配准时间相差为0.05 s，在小数点后精确5位的情况下配准误差同为0.089 79。但是随着点云数量的增加，改进的ICP算法与传统ICP算法相比具有明显优势，例如当初始点云数量为6 400时，传统ICP算法配准时间为16.00 s，配准误差为0.046 38，而改进ICP算法配准时间仅为2.40 s，配准误差为0.037 35；当初始点云数量为32 400时，改进算法优势更为突出。由表3数据分析可知，在不同点云数量下改进的ICP方法与传统ICP算法相比，无论是在配准时间还是在配准误差上都具有明显改进，并且随着初始点云数量的增加，本文改进方法的优势彰显得更为明显。

3结论

　　本文针对三维点云数据配准耗时长、精度低两方面的不足进行了相应改进，提出了一种改进特征点对选取方法，通过在经典点云Standford Bunny数据集上与采用传统ICP算法的配准结果相比，在配准时间和配准精度上都有明显提高。本文对点云数据配准的优化，对后续点云网格化以及场景重建提供了算法基础。

参考文献

　　［1］ TANG P B,HUBER D， AKINCI B， et al.Automatic reconstruction of asbuilt building information models from laserscanned point clouds:a review of related techniques［J］.Automation in Construction,2010,19(7):829-843.

　　［2］ 韩宝昌，曹俊杰，苏志勋.一种区域层次上的自动点云配准算法［J］.计算机辅助设计与图形学学报, 2015，27(2):313-

319.

　　［3］ BESL P J, MCKAY N D. Method for registration of 3D shapes［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence,1992，14(2):239-256.

　　［4］ Guo Yu, BENNAMOUN M, SHOEL F, et al.3D object recognition in cluttered scenes with local surface features: a survey［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014,36(11):2270-2287.

　　［5］ 杨小青, 杨秋翔，杨剑.基于法向量改进的ICP算法［J］.计算机工程与设计, 2016， 37(1):169-173.

　　［6］ 许斌, 李忠科，吕培军，等.基于特征的点云精确配准算法［J］.计算机应用与软件, 2013,30(11):112-115.

　　［7］ 张晓娟,李忠科，王先泽,等.基于特征点和改进ICP的三维点云数据配准算法［J］.传感器与微系统, 2012，31(9):116118.

　　［8］ KUIPERS J B. Quaternions and rotation sequences［M］.Sofia: Coral Press,2000:127-143.

　　［9］ HORN B K P.Closed-form solution of absolute orientation using unit quaternions［J］.Optical Society of America, 1987,4(4):629-642.

　　［10］ EGGERT D W, LORUSSO A.Estimating 3D rigid body transformations a comparison of four major algorithms［J］.Machine Vision and Applications, 1997,9(5):272-290.