王林,张一帆

　　（西安理工大学 自动化与信息工程学院，陕西 西安 710048）

        摘要：针对现有的社团检测算法存在准确度低、没有充分考虑到有向网络的方向特性等问题，提出一种改进的能够适用于有向网络的CNM（Newman 贪婪算法)社团检测算法。在算法设计中引入基于拓扑结构信息的有向网络节点相似度算法，并重新定义模块度增量函数ΔQs。使用一个计算机生成网络和两个实际网络对算法进行了测试并与已有算法进行比较。实验结果表明，文章提出的算法能够有效地检测出有向网络中的社团结构。

　　关键词：社团检测；有向网络；CNM算法；节点相似度

　　中图分类号：TP301.6文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.03.006

　　引用格式：王林,张一帆.基于节点相似度的有向网络社团检测算法［J］.微型机与应用，2017,36（3）：19-22.

0引言

　　社团检测是研究复杂网络结构和功能属性的一项最基本工作。社团可以看作是在网络中具有相似属性或者担任类似角色的节点的集合，这些社团内部的节点通常连接紧密，而社团之间的节点连接较为稀疏。为了发现网络中隐含的社团结构，传统的社团检测算法主要基于模块度指标，将社团检测问题转化为优化问题，然后搜索目标函数最优的社团结构，如经典的GN算法［1］和Newman快速算法［2］。然而，这类算法本身存在局限性［3］，而且上述算法并没有考虑到复杂网络存在有向性和节点的相似度属性。一方面，在现实世界的复杂网络中，连接关系并不总是无向的，如社交网络中的关注关系等；另一方面复杂网络中不同节点之间具有不同的相似度，相似度的大小体现出节点之间关联的紧密程度。

　　当前的社团检测算法除了传统基于模块度优化的方法［12,4］外，还包括考虑节点相似度、网络的有向性特征的算法。文献［5］在基于模块度指标的基础上，同时考虑节点相似度，提出一种SimilarityCNM算法，并指出CNM算法中模块度增量值的增加方向倾向于规模大的社团而忽略小规模社团，然而，该算法仅仅针对无向网络社团检测，并不能处理有向网络。考虑到有向网络这种更具有现实意义的网络，文献［6］利用基于局部信息的相似度计算方法将有向网络对称化为无向网络，再利用传统的无向网络社团检测算法划分出社团，然而该无向化方法破坏了有向网络的拓扑结构。文献［7］根据一个实际的有向网络——微博社交网络，提出一种基于共同关注和共同粉丝的微博用户相似度，在此基础上定义了新的模块度函数，采用Newman快速算法的思想进行社团检测。文献［8］提出了kPath共社团邻近相似性概念及计算方法，将有向网络社团检测问题转化为无向加权网络的社团检测问题。

　　综上所述，由于社团检测的基本思想是将属性或角色相似的节点划分到同一个集合中，考虑到基于模块度优化算法的局限性以及网络的有向交互性，本文基于CNM算法提出一种有向网络的社团检测算法。采用基于有向网络拓扑结构的相似度算法计算出节点相似度，接着利用相似度改进模块度增量函数，有效地克服了CNM算法本身贪婪思想以及模块度算法的局限性带来的社团划分不准确的缺点。

1相关理论与算法

　　1.1SimRank算法

　　SimRank［9］是一种有向图上基于图的拓扑结构信息来衡量任意两个对象间相似程度的模型，该模型的核心思想为：如果两个对象被其相似的对象所引用，那么这两个对象也相似。SimRank的基本公式:

　　其中，|I(v)|表示节点v的入度，Ii(v)表示v的第i个入邻居节点，c为衰减因子，且c∈(0,1)。

　　对于SimRank的迭代方程(1)能够最终迭代趋近于一个固定的值，采用如下迭代方式来进行SimRank的计算：

　　1.2CNM算法

　　为了提高社团检测的效率，降低计算复杂度，Clauset等人利用堆的数据结构来计算和更新网络的模块度，提出了一种新的贪婪算法，即为CNM算法［4］，该算法的复杂度只有O(nlog2n)，已接近线性复杂性。

　　CNM算法首先构造一个模块度增量矩阵ΔQi,j，然后通过对它的元素进行更新来得到模块度最大时的一种社团结构。算法的流程如下：（1）初始化网络中的每一个节点为一个社团；（2）计算网络中任意两个社团合并后的模块度增量ΔQi,j；（3）贪婪地选择ΔQi,j最大时的两个社团进行合并，更新与新社团相连接的所有社团的数据结构，再重复上一步过程；（4）当ΔQi,j<0时，算法终止。

　　1.3有向网络模块度

　　为了衡量社团检测的质量，Newman和Girvan定义了模块度函数，定量地描述网络中的社团，衡量网络社团结构的划分。考虑到有向网络的方向特性，在此基础上Leicht和Newman［10］提出适用于有向网络的模块度函数Qd，定义如下：

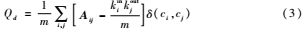
　　不同于有向网络模块度的是，Aij表示的是有向网络的邻接矩阵，kini与koutj分别表示节点的入度和出度。

2基于相似度的有向网络社团检测算法

　　本文算法的基本思想是利用节点之间相似度的变化来替代模块度的增量，合并规则仍然采用CNM算法的合并规则，最后得到若干个基于相似度的社团。

　　重新定义变量eij和ai为：

　　使用SimRank相似度替代模块度增量后的增量矩阵，定义如下：

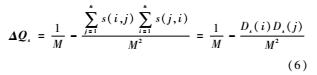
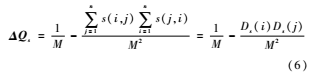
　　其中，n为网络中总的节点数，s(i,j)是节点i与j之间的SimRank相似度值，Ds(i)是节点i与其他节点之间相似度的总和，M是所有节点相似度的总和。

　　算法步骤如下：

　　输入：有向网络G(V,E)；

　　输出：社团的划分结果。

　　(1)使用SimRank算法对有向网络数据集进行相似度计算，得到节点之间的相似度矩阵S。

　　(2)对改进后的模块度增量矩阵ΔQs进行初始化。

　　(3)对算法中的最大堆结构H进行初始化，堆结构中存放的是ΔQs中每行的最大值。

　　(4)选择最大堆结构H中的堆顶元素，根据CNM算法的模块度增量更新规则对增量矩阵对应的行与列进行合并，并且对增量矩阵以及最大堆结构进行更新。

　　(5)所有的节点归于一个社团内，算法结束，否则继续进行步骤(4)。

3实验结果与分析

　　为了测试算法的有效性，本文使用一个计算机生成网络和两个真实网络进行验证。其中计算机生成网络采用LFR(LancichinettiFortunatoRadicchi)基准网络［1112］生成有向网络dirnet，真实网络采用poblogs［13］政治博客圈网络和wikivote［14］维基百科投票网络。

　　LFR基准网络是近年来社团检测中普遍应用的计算机生成模拟网络，通过设置不同的网络参数和社团参数来生成带有划分标准的复杂网络。该算法提供的社团划分标准即同时生成原始社团，解决了验证算法正确性的问题。使用LFR计算机生成网络时需要设置的主要参数如表1所示。

　　3.1计算机生成网络上的实验结果

　　在实验中，LFR计算机生成网络中的具体参数设置为：节点数N=62，平均入度数k=10，最大入度数kmax=16，混合参数mu=0.2，最小社团节点数cmin=9，最大社团节点数cmax=27。

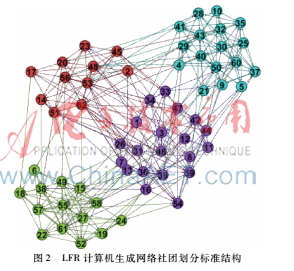
　　LFR计算机生成的初始有向网络如图1所示，其标准划分社团结构如图2所示。

　　利用本文提出的算法对LFR计算机生成网络进行社团检测，得出社团划分结果如表2所示。

　　可见本文算法的社团检测结果与图2中的标准社团划分结果相一致。利用式(3)计算出当前社团检测结果的模块度值为0.433，符合模块度取值范围，表明本文算法具有良好的准确性。

　　3.2算法中参数的选取

　　本文算法中，相似度的计算决定着最后的社团检测结果，对于SimRank算法，其中衰减因子参照文献［9］中的取值为c=0.8。SimRank的准确度是随着迭代次数k的增加而增加的，理论上当k趋于无穷大时准确度最高。鉴于真实网络大多为稀疏的［15］，在有限的迭代次数内能够及时收敛，因此可以通过实验选取最佳的k值。

　　选取poblogs和wikivote作为测试网络，对于不同的k值运行10次算法，分别计算迭代次数k取不同值时对应的模块度平均值。

　　如图3所示，模块度随着迭代次数的增加呈增长趋势，表明迭代使得社团结构更加明显。对于poblogs，k=5时，模块度有最大值Q=0.427，表现为两个明显的社团结构；对于wikivote，k=7时，模块度最大值Q=0.416。

　　3.3对比实验

　　在文献［4］中，Newman使用CNM算法分析了Amazon.com网上书店中页面的链接关系网络，该网络包含高达40万个节点和200多万条边，最终划分出10个社团。其中，最大社团包含114 538个节点，第二大的社团规模同样也不小，包含92 276个节点，而最小的社团只有947个节点。这样过大或者过小的社团规模有可能并不利于社团的发展。

　　利用本文算法与文献［10］中提出的有向网络社团检测算法在3个数据集上进行对比实验。

　　由表3数据可知，在LFR模型生成的dirnet网络中，由于在计算中充分考虑到有向网络的拓扑结构，本文算法比文献［10］中算法社团检测结果更好，而文献［10］中的算法是通过谱分析对有向模块度求解最大值，本身是一种模块度优化算法，并不能充分考虑到网络的结构。同样，在ploblogs数据集中，本文算法的社团检测结果也显示为两个社团，其中有15个节点没有被正确地划分，但模块度最优值为0.427，社团检测结果仍然表现出较好的社团结构。在wikivote数据集的实验中，使用本文算法虽然在模块度上比不上文献［10］的算法，但是检测出的社团规模均匀程度却比较好，在大规模的网络中，有时社团规模更加均匀。

4结束语

　　本文基于CNM算法提出了基于相似度的有向网络社团检测算法，与文献［10］提出的有向网络社团检测算法相比，不仅能够处理有向网络，而且检测出的社团规模也更加合理。实验结果表明，本文提出的算法不仅能够充分考虑到有向网络的拓扑结构信息，而且避免了模块度本身的局限性，使得划分出的社团规模更加均匀。

参考文献

　　［1］ GIRVAN M, NEWMAN M E J. Community structure in social and biological networks［J］. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12):7821-7826.

　　［2］ NEWMAN M E J.Fast algorithm for detecting community structure in networks［J］. Physica Review E, 2004, 69(6): 066133.

　　［3］ FORTUNATO S, BARTHLEMY M. Resolution limit in community detection［J］. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104(1):36-41.

　　［4］ CLAUSET A, NEWMAN M E, MOORE C. Finding community structure in very large networks.［J］. Physical Review E, 2010, 70(6):264-277.

　　［5］ ALFALAHI K, ATIF Y, HAROUS S. Community detection in social networks through similarity virtual networks［C］. IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, 2013:1116-1123.

　　［6］ ZHANG F, WU B, WANG B, et al. Community detection in directed graphs via node similarity computation［C］. IET International Conference on Wireless, Mobile and Multimedia Networks, 2013:258-261.

　　［7］ 孙怡帆, 李赛. 基于相似度的微博社交网络的社区发现方法［J］. 计算机研究与发展, 2014, 51(12):2797-2807.

　　［8］ 张海燕, 梁循, 周小平. 针对有向图的局部扩展的重叠社区发现算法［J］. 数据采集与处理, 2015,30(3):683693.

　　［9］ JEH G, WIDOM J. SimRank: a measure of structuralcontext similarity［C］. Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, 2002:538-543.

　　［10］ LEICHT E A, NEWMAN M E. Community structure in directed networks.［J］. Physical Review Letters, 2007, 100(11):2339-2340.

　　［11］ LANCICHINETTI A, FORTUNATO S, RADICCHI F. Benchmark graphs for testing community detection algorithms［J］. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2008, 78(2):561-570.

　　［12］ LANCICHINETTI A, FORTUNATO S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities［J］. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(2):145148.

　　［13］ ADAMIC L A, GLANCE N. The political blogosphere and the 2004 U.S. election: divided they blog［C］. International Workshop on Link Discovery, ACM, 2005:36-43.

　　［14］ LESKOVEC J, HUTTENLOCHER D, KLEIBERG J. Predicting positive and negative links in online social networks［J］. Computer Science, 2010,36(7):641-650.

　　［15］ Chen Jie, SAAD Y. Dense subgraph extraction with application to community detection［J］.IEEE Transactions on Knowledge & Data Engineering, 2012, 24(7): 1216-1230.