张存生，张德学，韩学森，王超，张恒，冀贞贤

　　（山东科技大学 电子通信与物理学院，山东 青岛 266590）

       摘要：直接频率合成技术（DDS）是无线通信中的关键技术，因应用场合及技术指标不同，DDS中的正弦波形产生模块有多种实现方法，本设计采用CORDIC算法计算波形数据，并通过预处理实现全部相位波形数据的即时计算，不占用存储资源，且可通过改变迭代次数来调节精度。所设计的DDS精度、频率、相位可调，在Altera Cyclone2中实现时，时钟频率可达172 MHz，占用1 171 LUTs。

　　关键词：FPGA；直接频率合成技术；CORDIC

　　中图分类号：TN99文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.04.018

　　引用格式：张存生，张德学，韩学森，等.基于CORDIC算法的参数可调信号源设计［J］.微型机与应用，2017,36（4）：59-62.

0引言

　　直接频率合成技术(Direct Digital Synthesizer，DDS)是电子系统的重要组成部分，也是无线通信中关键技术。在数字混频中，DDS产生正弦信号与输入信号进行相乘可以实现信号调制的效果。目前，通过现场可编程门阵列 (Field Programmable Gate Array，FPGA)实现DDS有三种途径：基于无限冲激响应 (Infinite Impulse Response，IIR)滤波器的实现方法、基于查找表 (Look Up Table，LUT)的实现方法以及基于坐标旋转数字计算机 (Coordinate Rotation Digital Computer，CORDIC)算法的实现方法［1］。基于IIR滤波器的实现方法用到大量乘法器，不利于FPGA实现，基于查找表的实现方法用到大量ROM资源，而CORDIC算法只需要简单移位操作和加减操作就可以计算正余弦值，可用FPGA高效实现。CORDIC 算法是一种用于计算一些常用的基本运算函数和算术操作的循环迭代算法［2］。

　　本设计基于CORDIC算法设计DDS，产生正余弦信号，并通过改变输入信号FWWORD、PH_ADJ_EN、PH_ADJ和DATA_ACC_SEL达到频率和相位可调以及输出数据精度可调的效果。AD9850芯片可以实现相位的调节，但是其调节有最小量为11.25°的限制。本设计可以在运行阶段将相位在［-180°，180°］之间任意调节，同时可以对数据精度和输出波形频率进行调节。用Verilog编写代码，使用Modelsim完成代码仿真，使用Altera的EP2C70F89C6芯片进行资源评估。

1DDS的结构

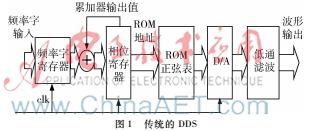
　　图1传统的DDS传统DDS采取查找表方式进行设计，将相位对应值预先存储在ROM中，通过地址控制找到相位对应正余弦值，从而产生正余弦波形。这种方式会用到大量ROM资源。传统DDS设计见图1。本文基于CORDIC算法设计DDS，通过改变输入信号FWWORD、PH_ADJ_EN、PH_ADJ和DATA_ACC_SEL实现波形频率、波形相位和数据精度可调，同时不使用ROM资源，其中FWWORD调节波形频率、PH_ADJ_EN和PH_ADJ共同调节相位，DATA_ACC_SEL通过选择不同迭代次数的迭代数据改变输出数据的精度。

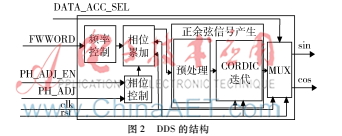
　　本设计主要包括相位累加、频率控制、相位控制、CORDIC预处理、CORDIC迭代和迭代次数选择模块，结构如图2所示。其中通过CORDIC预处理和迭代部分求出每个相位对应正余弦值，并将计算结果输出。在相位累加部分，通过相位不断循环累加获得［-180o，180o］之间的相位，将累加相位数据送到CORDIC算法模块，进而得到连续输出的正余弦函数值，获得正交正余弦波形。迭代次数选择模块则可以选择不同迭代次数进而改变输出数据的精度。与参考文献［2］和［3］相比，加入了数据精度、波形相位和波形频率调节部分。与AD9850芯片相比，相位调节不再受到限制，并且输出数据精度可以调节。

2CORDIC算法［1，4］

　　CORDIC算法可以用来直接计算正余弦函数、乘除法以及双曲函数。经过发展CORDIC算法已经发展成为拥有圆周系统、线性系统和双曲系统的一个算法系统。每种系统中又包含旋转模式和向量模式两种不同的计算模式。本设计采用圆周系统中旋转模式计算正余弦值，获得相位对应正余弦值。为了保证数据在量化后没有溢出，CORDIC算法迭代部分输入信号采用16位有符号数，迭代次数由DATA_ACC_SEL决定，最多为16次。

　　2.1算法迭代原理

　　圆周系统旋转模式矢量旋转图如图3所示。

　　根据图3可知P点的坐标如下：

　　xP=cosα

　　yP=sinα(1)

　　逆时针旋转β得到的Q点坐标为：

　　xQ=cos(α+β)

　　yQ=sin(α+β)（2）

　　展开可得：

　　xQ=cosαcosβ－sinαsinβ

　　yQ=sinαcosβ+cosαsinβ（3）

　　将式（1）代入式（3）可得：

　　xQ=xPcosβ－yPsinβ

　　yQ=yPcosβ+xPsinβ（4）

　　提出cosβ可得：

　　xQ=cosβ(xP－yPtanβ)

　　yQ=cosβ(yP+xPtanβ)（5）

　　如果去掉cosβ可以得到R的坐标：

　　xR=xP－yPtanβ

　　yR=yP+xPtanβ(6）

　　将β分成若干次叠加，那么每次的叠加结果与上次的关系为：

　　xi+1=xi－yitanβi

　　yi+1=yi+xitanβi（7）

　　不妨令

　　βi=tan－1(di2－i)（8）

　　将式（8）代入式（7）可得：

　　xi+1=xi－diyi2－i

　　yi+1=yi+dixi2－i（9）

　　为了确定di的符号，引入变量Z，并给出如下关系:

　　zi+1=zi－ditan－12－i(10)

　　得到圆周系统旋转模式下的迭代方程如下：

　　xi+1=xi－diyi2－i

　　yi+1=yi+dixi2－i

　　zi+1=zi－ditan－12－i

　　di=+1,zi≥0

　　－1,zi<0（11）

　　式（11）没有考虑到模长处理。引入模长补偿因子An。在圆周系统旋转模式下，最终迭代的目标是使得Zn=0，最终得到圆周系统旋转模式公式如下：

　　根据式（12）和式（13）可知，给定初始值x0和y0，并根据迭代次数确定An，利用CORDIC迭代算法，可得Z0对应的正弦值和余弦值。

　　对应式（11）的并行架构设计如图4所示。参考XILINX CORDIC IP［5］核的设计，本次设计迭代次数最多为16次，CORDIC迭代模块是16位有符号数。

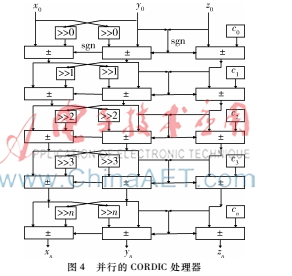
　　经过计算式（8）可以知道β的累加结果在 ［-99.88°，99.88°］之间，即可以直接计算角度在［-99.88°，99.88°］之间，不在该范围内的相位，需要对其进行预处理。

　　2.2预处理原理

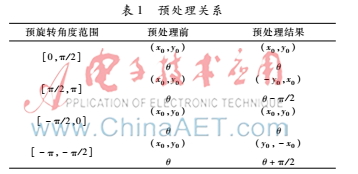
　　根据三角函数的性质，对不能直接计算的相位值进行预处理。CORDIC算法的预处理关系见表1。其中（x0，y0）是预处理之前的坐标，θ是要进行处理的角度。在预处理结果一列中是对应的处理后的结果。引入变量W，根据预处理对应关系可以得到：

　　xpre=－σy0

　　ypre=σx0

　　Wpre=W0－σ·π/2

　　σ=sign(z0)(14)

3仿真结果及资源评估

　　3.1仿真结果

　　CORDIC迭代模块输入采用弧度输入，并对输入进行量化处理，扩大214倍，输出结果也将扩大214倍。通过时钟驱动相位累加模块，产生连续相位。

　　FWWORD为17位有符号数，数据范围在［-65 536,65 535］之间。PH_ADJ为17位有符号数，相位调节范围在［-65 536,65 535］之间，量化后CORDIC模块的输入值范围在［-51 472,51 472］之间，因此，PH_ADJ可以进行［-51 472,51 472］之间的任意相位调节。DATA_ACC_SEL的位宽是2，可以选择迭代7次、10次、13次或16次。

　　使用Modelsim对设计做仿真，图5给出了在迭代次数为16时，对相位和频率调节测试的波形。测试开始时频率累加步长为10，初始相位为0。第一次调整将相位累加步长改为20，相位不做调整。第二次累加步长不做调整，将相位调节到-90°。第三次将累加步长调节为30，同时将相位调节到90°。经过三次测试可知，该设计可以产生正交正余弦波形，同时，可以对产生波形的频率和相位进行调整，并且对单个参数进行调整时，其他参数不受影响。FWWORD对频率进行调节，PH_ADJ_EN和PH_ADJ对相位进行调节，同时相位的调节不会受到限制。　

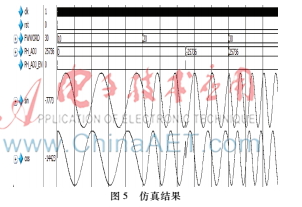
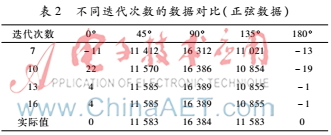
　　表2给出了在累加步长为10、初始相位为0时，不同迭代次数产生的数据。其中迭代次数有7次、10次、13次和16次。表中的实际值是真实数据扩大214倍之后的数据。根据表中数据可知，不同的迭代次数产生的数据精度是不同的，本设计中DATA_ACC_SEL信号可以选择不同迭代次数的迭代结果，进而改变数据的输出精度。在13次和16次的迭代中数据是一样的，说明在数据位宽一定的情况下，数据的最大迭代次数是一定的。

　　3.2资源评估

　　采用Quartus Ⅱ 13设计RTL代码，并在Altera的EP2C70F89C6 FPGA芯片上实现，评估资源利用率和最大工作频率，与文献［3］使用的芯片相同。本设计与文献［3］中的传统设计及优化后的设计资源对比见表3。由表3可知，本设计在加入数据精度调节、相位和频率调节后与传统设计的资源使用［3］相当，且不占用block memory。测得本设计的最大工作频率可达172.83 MHz高于AD8950的最大工作频率125 MHz。

4结论

　　本设计基于CORDIC算法进行DDS设计，对设计进行Modelsim仿真，通过调节输入信号FWWORD、PH_ADJ_EN、PH_ADJ和DATA_ACC_SEL能够达到相位和频率可调以及输出数据精度可调的效果。

　　采用Quartus Ⅱ 13设计RTL代码，并用Altera的EP2C70F89C6 FPGA芯片进行资源评估，在加入数据精度调节、相位和频率调节后与传统设计的资源使用情况相当，并且没有使用到ROM资源，节省了ROM资源。

　　参考文献

　　［1］ 高亚军.基于FPGA的数字信号处理（第二版）［M］.北京：电子工业出版社，2015.

　　［2］ 景标，邢维巍，张燕琴.基于 CORDIC 算法的正交信号源实现［J］.现代电子技术，2016，39(7)：57-59.

　　［3］ 常柯阳，曾岳南，陈平，等.CORDIC算法在正余弦函数中的应用及其 FPGA实现［J］.计算机工程与应用，2013,49(7)：140-143.

　　［4］ 李庆华.通信IC设计(上册)［M］.北京：机械工业出版社，2016.

　　［5］ 刘东华.Xilinx系列FPGA芯片IP核详解［M］.北京：电子工业出版社，2013.